LM算法
最小二乘法的概念
最小二乘法要关心的是对应的cost function是线性还是非线性函数,不同的方法计算效率如何,要不要求逆,矩阵的维数
一般都是过约束,方程式的数目多于未知的参数数目。
最小二乘法的目标:求误差的最小平方和,根据cost function的对应有两种:线性和非线性(取决于对应的残差(residual)是线性的还是非线性的)。
-
线性最小二乘的解是closed-form solution 即 \(x = (A^TA)^{-1}A^Tb\)
\(S(x) = ||b -Ax ||^2 = (b -Ax)^T(b -Ax) = b^Tb - b^TAx - x^TA^Tb + x^TA^TAx\)
Note that :\((b^TAx)^T = x^TA^Tb\) 的维数是 1*1(y的列数目).所以 \(b^TAx = x^TA^Tb\)
\(S(x) = b^Tb - 2b^TAx + x^TA^TAx\)
对\(x\)求导
\(-2A^Tb + 2 (A^TA)x = 0\)
\(x = (A^TA)^{-1}A^Tb\)
-
而非线性最小二乘没有closed-form,通常用迭代法求解。在每次迭代的过程使用一个线性化的方程代替计算。
有牛顿法,牛顿高斯法,LM, 其实可以分为trust region 和 linear line search
非线性最小二乘法的方法有
迭代法,即在每一步update未知量逐渐逼近解,cost function在下降,可以用于各种各样的问题。
- 梯度下降(最速下降法)是迭代法的一种,可以用于求解最小二乘问题
\(f(x + \alpha \overrightarrow d) = f(x_0) + \alpha f'(x_0)\overrightarrow d + \text {二阶以上无穷小}\)
上面的\(x_0\)是泰勒展开式的点, \(\alpha\)是 步长(一个实数) , $ \overrightarrow d$ 单位方向(一个向量),即 \(|\overrightarrow d| = 1\)
显然当\(d\)的方向和\(f'(x_0)\)方向相反的时候,\(cos180 =-1\),整体取到最小值。这就是为什么取的是梯度的反方向原因。
当然上面的步长一般也是可以求得,怎么求步长也是一门学问。
下面的都是从牛顿法引申出来的,记住牛顿法求得是稳定点\(f'(x) = 0\),导数为0的不一定是最小值,梯度下降法求得是局部最小值,从计算上看
- 牛顿法 泰勒展开式到二阶,
求导就有,\(\frac{\partial f}{\partial x_t} = g + H(x_{t+1} -x_t)\),让他为0,就有了牛顿公式
要是H是正定的,上面的就是凸函数,也就一定有了最小值。可惜H不一定是正定的,这就引导出了下面的方法
- 高斯-牛顿法
是另一种经常用于求解非线性最小二乘的迭代法(一定程度上可视为标准非线性最小二乘求解方法)。
我们优化的cost function是 $$min \sum _i r_i(x)^2$$
根据上面的牛顿法:
梯度的表示
Hessian矩阵的表示
要是把上面公式的最后一项去掉,至少是半正定了,而且不用计算Hessain矩阵了,这就是牛顿高斯法
在什么情况下,去掉最后一项比较好,
- residual(\(r_i\))小的时候
- 或者接近linear ,这样一阶微分是常数,二阶微分就是0
上面两种情况下,第二项都很小,公式如下
- Levenberg-Marquardt
的迭代法用于求解非线性最小二乘问题,就结合了梯度下降和高斯-牛顿法。
总结
所以如果把最小二乘看做是优化问题的话,那么梯度下降是求解方法的一种,\(x=(A^TA)^{-1}A^Tb\)是求解线性最小二乘的一种,高斯-牛顿法和Levenberg-Marquardt则能用于求解非线性最小二乘。
LM算法相对于高斯牛顿算法和梯度下降的优缺点
-
首先梯度下降法和高斯牛顿法都是最优化方法。其区别之处在于,
-
梯度下降法在寻找目标函数极小值时,是沿着反梯度方向进行寻找的。梯度的定义就是指向标量场增长最快的方向,在寻找极小值时,先随便定初始点(x0,y0)然后进行迭代不断寻找直到梯度的模达到预设的要求。但是梯度下降法的缺点之处在于:在远离极小值的地方下降很快,而在靠近极小值的地方下降很慢,靠近的时候可能成zig-zag下降。
-
而高斯牛顿法是一种非线性最小二乘最优化方法。其利用了目标函数的泰勒展开式把非线性函数的最小二乘化问题化为每次迭代的线性函数的最小二乘化问题。高斯牛顿法的缺点在于:若初始点距离极小值点过远,迭代步长过大会导致迭代下一代的函数值不一定小于上一代的函数值。
-
LM算法在高斯牛顿法中加入了因子
μ,当μ大时相当于梯度下降法,μ小时相当于高斯牛顿法。在使用Levenberg-Marquart时,先设置一个比较小的μ值,当发现目标函数反而增大时,将μ增大使用梯度下降法快速寻找,然后再将μ减小使用牛顿法进行寻找。
-
The Gauss–Newton algorithm is used to solve non-linear least squares problems.
It is a modification of Newton's method for finding a minimum of a function.
Unlike Newton's method, the Gauss–Newton algorithm can only be used to minimize a sum
of squared function values, but it has the advantage that second derivatives, which
can be challenging to compute, are not required.
However, as for many fitting algorithms, the LMA finds only a local minimum,
which is not necessarily the global minimum.
% 计算函数f的雅克比矩阵
syms a b y x real;
f=a*cos(b*x) + b*sin(a*x)
Jsym=jacobian(f,[a b])
data_1=[ 0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0, 2.2, 2.4, 2.6, 2.8, 3.0,3.2, 3.4, 3.6, 3.8, 4.0, 4.2, 4.4, 4.6, 4.8, 5.0, 5.2, 5.4, 5.6, 5.8, 6.0, 6.2 ];
obs_1=[102.225 ,99.815,-21.585,-35.099, 2.523,-38.865,-39.020, 89.147, 125.249,-63.405, -183.606, -11.287,197.627, 98.355, -131.977, -129.887, 52.596, 101.193,5.412, -20.805, 6.549, -40.176, -71.425, 57.366, 153.032,5.301, -183.830, -84.612, 159.602, 155.021, -73.318, -146.955];
% 2. LM算法
% 初始猜测初始点
a0=100; b0=100;
y_init = a0*cos(b0*data_1) + b0*sin(a0*data_1);
% 数据个数
Ndata=length(obs_1);
% 参数维数
Nparams=2;
% 迭代最大次数
n_iters=60;
% LM算法的阻尼系数初值
lamda=0.1;
%LM算法的精度
ep=100
% step1: 变量赋值
updateJ=1;
a_est=a0;
b_est=b0;
% step2: 迭代
for it=1:n_iters
if updateJ==1
% 根据当前估计值,计算雅克比矩阵
J=zeros(Ndata,Nparams);
for i=1:length(data_1)
J(i,:)=[cos(b_est*data_1(i))+data_1(i)*b_est*cos(a_est*data_1(i)) -sin(b_est*data_1(i))*a_est*data_1(i)+sin(a_est*data_1(i)) ];
end
% 根据当前参数,得到函数值
y_est = a_est*cos(b_est*data_1) + b_est*sin(a_est*data_1);
% 计算误差
d=obs_1-y_est;
% 计算(拟)海塞矩阵
H=J'*J;
% 若是第一次迭代,计算误差
if it==1
e=dot(d,d);
end
end
% 根据阻尼系数lamda混合得到H矩阵
H_lm=H+(lamda*eye(Nparams,Nparams));
% 计算步长dp,并根据步长计算新的可能的\参数估计值
dp=inv(H_lm)*(J'*d(:));
%求误差大小
g = J'*d(:);
a_lm=a_est+dp(1);
b_lm=b_est+dp(2);
% 计算新的可能估计值对应的y和计算残差e
y_est_lm = a_lm*cos(b_lm*data_1) + b_lm*sin(a_lm*data_1);
d_lm=obs_1-y_est_lm;
e_lm=dot(d_lm,d_lm);
% 根据误差,决定如何更新参数和阻尼系数
if e_lm<e
if e_lm<ep
break
else
lamda=lamda/5;
a_est=a_lm;
b_est=b_lm;
e=e_lm;
disp(e);
updateJ=1;
end
else
updateJ=0;
lamda=lamda*5;
end
end
%显示优化的结果
a_est
b_est
plot(data_1,obs_1,'r')
hold on
plot(data_1,a_est*cos(b_est*data_1) + b_est*sin(a_est*data_1),'g')

#pragma once
#include <stdio.h>
#include <opencv2\core\core.hpp>
#include <iostream>
using namespace std;
using namespace cv;
const int MAXTIME = 50;
#pragma comment(lib,"opencv_core249d.lib")
Mat cvSinMat(Mat a)
{
int rows = a.rows;
int cols = a.cols;
Mat out(rows, cols, CV_64F);
for (int i = 0; i < rows; i++)
{
out.at<double>(i, 0) = sin(a.at<double>(i, 0));
}
return out;
}
Mat cvCosMat(Mat a)
{
int rows = a.rows;
int cols = a.cols;
Mat out(rows, cols, CV_64F);
for (int i = 0; i < rows; i++)
{
out.at<double>(i, 0) = cos(a.at<double>(i, 0));
}
return out;
}
Mat jacobin(const Mat& pk, const Mat& x) // pk= [a,b] a*cos(b*x) + b*sin(a*x)
{
Mat_<double> J(x.rows, pk.rows), Sa, Sb ,Ca, Cb,da, db;
Sa = cvSinMat(pk.at<double>(0)*x);
Sb = cvSinMat(pk.at<double>(1)*x);
Ca = cvCosMat(pk.at<double>(0)*x);
Cb = cvCosMat(pk.at<double>(1)*x);
da = Cb + x.mul(pk.at<double>(1)*Ca);
db = Sa - x.mul(pk.at<double>(0)*Sb);
//cout << "da= " << da << endl;
da.copyTo(J(Rect(0, 0, 1, J.rows)));
db.copyTo(J(Rect(1,0, 1, J.rows)));
return J;
}
Mat yEstimate(const Mat& pk, const Mat& x)
{
Mat_<double> Y(x.rows, x.cols),Cb,Sa;
Sa = cvSinMat(pk.at<double>(0)*x);
Cb = cvCosMat(pk.at<double>(1)*x);
Y = pk.at<double>(0)*Cb + pk.at<double>(1)*Sa;
return Y;
}
void LM(double* p0, int pN, double* x, int xN, double* y, double lamda, double step, double ep = 0.000001)
{
int iters = 0;
int updateJ = 1;
double ek = 0.0, ekk = 0.0;//估计误差
Mat_<double> xM(xN, 1, x), yM(xN, 1, y), pM(pN, 1, p0), JM, yEM, yEMM, dM, gM, dMM, dpM;//至少需要JM,gM,dpM,pM
for (; iters < MAXTIME; iters++)
{
if (updateJ == 1)
{
JM = jacobin(pM, xM); //雅克比矩阵
//outData(fs, JM, "J.xml");
yEM = yEstimate(pM, xM); //f(β)
dM = yM - yEM; // y-f(β)
gM = JM.t()*dM; //
if (iters == 0)
ek = dM.dot(dM); //第一次 直接||r||^2
}
Mat_<double> NM = JM.t()*JM + lamda*(Mat::eye(pN, pN, CV_64F)); //J(T)J + lambda*I
if (solve(NM, gM, dpM)) //
{
Mat_<double> pMM = pM + dpM; //更新最小值
yEMM = yEstimate(pMM, xM);
dMM = yM - yEMM;
ekk = dMM.dot(dMM);
if (ekk < ek)//成功则更新向量与估计误差
{
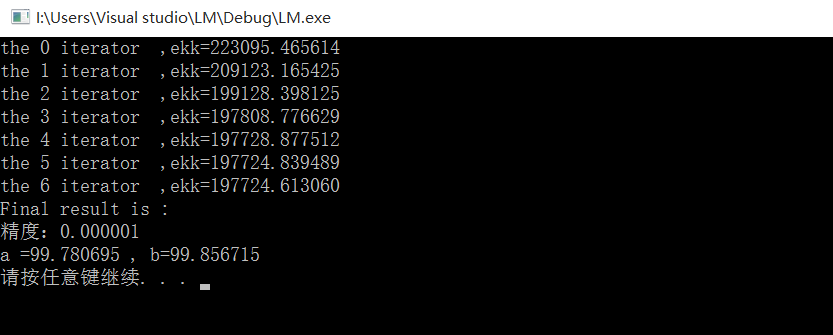
printf("the %d iterator ,ekk=%lf \n", iters,ekk);
if (dpM.dot(dpM) < ep)
{
printf("Final result is :\n");
printf("精度:0.000001\n");
printf("a =%lf , b=%lf\n", pMM.at<double>(0),pMM.at<double>(1));
return;
}
else
{
pM = pMM;
ek = ekk;
lamda = lamda / step;
updateJ = 1;
continue;
}
}
else //if an iteration gives insufficient reduction in the residual, λ(lamda) can be increased
{
printf("the %d iterator \n", iters);
lamda = lamda*step;
updateJ = 0;
}
}
else
{
printf("the solve invertx matrix error\n");
}
}
}
#include "LM.h"
int main()
{
double data[] = { 0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0, 2.2, 2.4, 2.6, 2.8, 3.0,
3.2, 3.4, 3.6, 3.8, 4.0, 4.2, 4.4, 4.6, 4.8, 5.0, 5.2, 5.4, 5.6, 5.8, 6.0, 6.2 };
double obs[] = { 102.225 ,99.815,-21.585,-35.099, 2.523,-38.865,
-39.020, 89.147, 125.249,-63.405, -183.606, -11.287,
197.627, 98.355, -131.977, -129.887, 52.596, 101.193,
5.412, -20.805, 6.549, -40.176, -71.425, 57.366, 153.032,
5.301, -183.830, -84.612, 159.602, 155.021, -73.318, -146.955 };
//初始点
double p0[] = { 100, 100 };
LM(p0, 2, data, 32, obs, 0.1, 10);
system("pause");
}