一个矩形面积放入一个大的矩形面积能放多少个不重叠

背景：

　　我们先从小范围的来说，把一个矩形面积放到一个大的矩形面积里，我想得到一个比较优良的摆放方式以及知道他摆放的个数

分析考虑：

　　通过图形在纸上画出逻辑，假设现在有一个10*15的矩形平面，现在把这个平面放入到一个200*200的矩形平面里面，要求不能重合，形状不能变异，只能是面积和面积之间的拼接，需要考虑到几种摆放方式

解决方案

       起初我是在脑海里分析，然后通过画图方式，把摆放的方式画到纸上，然后通过分析多种摆放方式，找出他们的共性，同时通过代码进行实现和验证，通过多次不同的参数反复的验证和计算，获得算法的正确性，从而得到数量较多的一种逻辑方法，此方法可以理解为合并法，我通过把大的容器面积拆分成两个面积，从而得到两个面积内的数量合并得到最终的数量。为什么会要拆分成两个呢，这里面就考虑了矩形面积可以改变方向摆放，通过画图分析可以得出4种摆放方式。

      

 

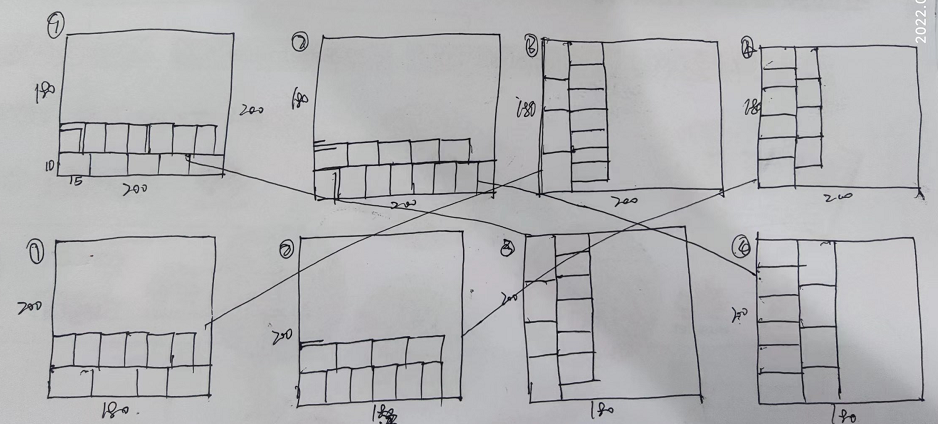
 　　起初是画出8个图，但是通过分析发现其中有4种是重复的，所以画线部分就是一一对应的，所以我最后写出4种图形的编码。

 

代码案例

　　

        /// <summary>
        /// 方案综合
        /// </summary>
        /// <param name="mAreaLength"></param>
        /// <param name="mAreaWidth"></param>
        /// <param name="lAreaLength"></param>
        /// <param name="lAreaWidth"></param>
        /// <returns></returns>
        public static long GetPutCountByMethod(long mAreaLength, long mAreaWidth, long lAreaLength, long lAreaWidth)
        {

            var lengthCount = lAreaLength / mAreaLength;
            var widthCount = lAreaWidth / mAreaWidth;
            //求最后宽边剩下的面积是否可以摆放箱子
            long yuCount = 0;
            var leftYu = lAreaWidth - (widthCount * mAreaWidth);
            if (leftYu >= mAreaLength && lAreaLength >= mAreaWidth)
            {
                //表示阴影部分还是可以摆放
                var leftLengthCount = lAreaLength / mAreaWidth;
                var leftWidthCount = leftYu / mAreaLength;
                yuCount += leftLengthCount * leftWidthCount;
            }
            var rigthYu = lAreaLength - (lengthCount * mAreaLength);
            if (rigthYu >= mAreaWidth && lAreaWidth >= mAreaLength)
            {
                //表示阴影部分还是可以摆放
                var rigthLengthCount = rigthYu / mAreaWidth;
                var rigthWidthCount = lAreaWidth / mAreaLength;
                yuCount += rigthLengthCount * rigthWidthCount;
            }
            var count = lengthCount * widthCount + yuCount;
            return count;
        }

        /// <summary>
        /// 方案综合 
        /// </summary>
        /// <param name="areaEntity"></param>
        /// <param name="containerAreaEntity"></param>
        /// <returns></returns>
        public static long GetPutCountByMethod(AreaEntity areaEntity, AreaEntity containerAreaEntity)
        {
            var baseCount1 = GetPutCountByMethod(areaEntity.Length, areaEntity.Width, containerAreaEntity.Length, containerAreaEntity.Width);
            var baseCount2 = GetPutCountByMethod(areaEntity.Width, areaEntity.Length, containerAreaEntity.Length, containerAreaEntity.Width);
            var countList = new List<long>();
            countList.Add(baseCount1);
            countList.Add(baseCount2);
            for (int i = 1; i <= containerAreaEntity.Width / areaEntity.Width; i++)
            {
                if (areaEntity.Width * i <= containerAreaEntity.Width)
                {
                    var beginCount1 = GetPutCountByMethod(areaEntity.Length, areaEntity.Width, containerAreaEntity.Length, areaEntity.Width * i);
                    var endCount1 = GetPutCountByMethod(areaEntity.Width, areaEntity.Length, containerAreaEntity.Length, containerAreaEntity.Width - areaEntity.Width * i);
                    var count1 = beginCount1 + endCount1;
                    countList.Add(count1);
                }
            }

            for (int i = 1; i <= containerAreaEntity.Width / areaEntity.Length; i++)
            {
                if (areaEntity.Length * i <= containerAreaEntity.Width)
                {
                    var beginCount2 = GetPutCountByMethod(areaEntity.Width, areaEntity.Length, containerAreaEntity.Length, areaEntity.Length * i);
                    var endCount2 = GetPutCountByMethod(areaEntity.Length, areaEntity.Width, containerAreaEntity.Length, containerAreaEntity.Width - areaEntity.Length * i);
                    var count2 = beginCount2 + endCount2;
                    countList.Add(count2);
                }
            }

            for (int i = 1; i <= containerAreaEntity.Length / areaEntity.Width; i++)
            {
                if (areaEntity.Width * i <= containerAreaEntity.Length)
                {
                    var beginCount3 = GetPutCountByMethod(areaEntity.Length, areaEntity.Width, areaEntity.Width * i, containerAreaEntity.Width);
                    var endCount3 = GetPutCountByMethod(areaEntity.Width, areaEntity.Length, containerAreaEntity.Length - areaEntity.Width * i, containerAreaEntity.Width);
                    var count3 = beginCount3 + endCount3;
                    countList.Add(count3);
                } 
            }

            for (int i = 1; i <= containerAreaEntity.Length / areaEntity.Length; i++)
            {
                if (areaEntity.Length * i <= containerAreaEntity.Length)
                {
                    var beginCount4 = GetPutCountByMethod(areaEntity.Width, areaEntity.Length, areaEntity.Length * i, containerAreaEntity.Width);
                    var endCount4 = GetPutCountByMethod(areaEntity.Length, areaEntity.Width, containerAreaEntity.Length - areaEntity.Length * i, containerAreaEntity.Width);
                    var count4 = beginCount4 + endCount4;
                    countList.Add(count4);
                }
            }

            countList.Sort();
            return countList[countList.Count() - 1];
        }

 

看到的代码是我需求的一部分，这里就是4种方法的摆放循环，得出每一次计算的结果，最终取数值最大的一个