Depth from Videos in the Wild 解读

2019年7月17日11:37:05

论文 Depth from Videos in the Wild: Unsupervised Monocular Depth Learning from Unknown Cameras

主要有几个亮点：

1，处理移动物体时 instance segmentation and tracking are not required，不需要实例分割，

　　虽然文章里说还是需要一个网络预测可能移动的区域，但比起需要实例分割，难度还是下降了点。

2，occlusion-aware consistency 遮挡情形下的深度预测一致性

3，能够通过网络学习内参

这篇文章还是有点干货的，毕竟谷歌出品。

 

 

先讨论第二点，遮挡情形下的深度预测的问题

这里很好理解也比较好实现：

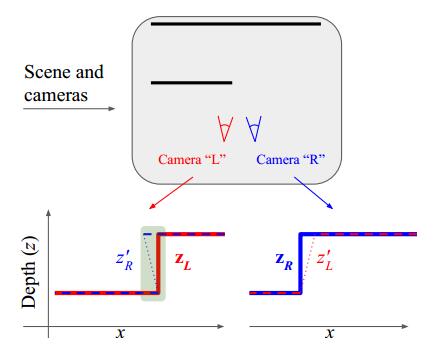
左右两个相机对同一个场景进行观察，但是因为存在遮挡的原因，左右两个相机对

同一个三维点的深度预测结果不一致。这些遮挡区域有什么特点呢？

左右两个相机对同一个三维点的预测深度分别为$\mathbf{z}_{L}$和$\mathbf{z}_{R}$

然后

把$\mathbf{z}_{L}$变换(warp)到右相机所在的位置得到深度$z_{L}^{\prime}$

把$\mathbf{z}_{R}$变换到左相机所在的位置得到深度$z_{R}^{\prime}$

we apply photometric and geometric losses only at pixels where $z_{R}^{\prime} \leq \mathbf{z}_{R}$

and $z_{L}^{\prime} \leq \mathbf{z}_{L}$.

只在 $z_{R}^{\prime} \leq \mathbf{z}_{R}$ 和 $z_{L}^{\prime} \leq \mathbf{z}_{L}$的区域计算 photometric 和 geometric losses。

 

 

为什么是这些区域?

理想情况如下：

 

 

 

 

 

 

 

 

 

 

 

 

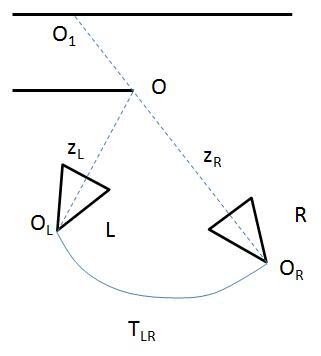
左相机L和右相机R观察同一个三维点O。

O到左相机的光心$O_L$距离为$z_L$，右相机类似。

从右相机到左相机的变换为$T_{LR}$，因此有如下关系：

$z_{R}^{\prime} = z_L=T_{LR}*z_R$

$z_{L}^{\prime} = z_R=T_{RL}*z_L$

也就是说，在两个不同的位置观察到的同一个三维点的深度$z_L$和$z_R$看起来大小

不一样，但是换算到到对方的位置后，应该是相等的。

下面是有遮挡的情况中的一种(右相机看的到，左相机看不到):

 

 

 

 

 

 

 

 

 

 

 

 

 

这里就不仅要像sfmlearner中做warp ref img to tgt ，还要在两个相机位置上互相warp深度图，

再把上述区域剔除出计算loss的部分。

深度不一致，一是因为有遮挡，二是因为这个三维点在运动。

 

 

 

 

 

所以这个方式对于处理移动物体的深度预测也是有帮助的

总的来讲就是要让loss计算的更清楚，把不该计算的部分剔除出去。

 

想了一下，warp ref_img和warp 深度图Z是一样的，利用现有设施简单改造下

就可以达到目标。

 

2019年7月19日23:42:42

遮挡的处理会干扰ssim的计算。。。

 

 

 

 

 

 

 

 

做法是当两帧之间的depth discrepancy 相比 depth discrepancy 的RMS较大

的时候，降低ssim在这个区域的权重？

 

2019年7月20日10:13:56

关于内参的学习，之前在sfmlearner剖析的博客中简单推导了一下公式，

这篇文章中不用T，用(R*XYZ+t)的写法替换，其他都是一样的，写成：

$depth_2*uv_2 = K\left(R*XYZ_1+t\right)$

$depth_2*uv_2 = K*R*depth_1*K^{-1}*uv_1+K*t$

调整下$depth_1$的顺序：

$$ depth_2*uv_2 = K*R*K^{-1}*depth_1*uv_1+K*t \tag{0} $$

这个就是论文中的方程1：

$$ z^{\prime} p^{\prime}=K R K^{-1} z p+K t \tag{1}$$

这里就没有把$depth_2$省略。

 

方程1的好处就是图片中的每个像素都要符合这个方程：

$z^{\prime}\left[\begin{array}{l}{u_2} \\ {v_2} \\ {1}\end{array}\right]= K R K^{-1} z\left[\begin{array}{l}{u_1} \\ {v_1} \\ {1}\end{array}\right]+K t $

也就是说，误差信号在反向传播时也能传导到每个像素。

然后

$K=\left(\begin{array}{ccc}{f_{x}} & {0} & {x_{0}} \\ {0} & {f_{y}} & {y_{0}} \\ {0} & {0} & {1}\end{array}\right)$

文章然后说了t提供不了内参学习时的监督信息，而且有可能产生假的解，又说了旋转信号R可以

提供内参学习时的监督信息，

附录A.2的推导解释了当旋转矩阵不为单位矩阵时，学出来的内参K会是正确的、唯一的。

Mathematically, $R = I$ provides no supervision signal for K, whereas $R \neq I$ provides a complete supervision siglal for it.

为了简化起见，假设相机只有绕y轴的旋转，且没有平移，则方程1简化成：

$$\Delta p_{x}=r_{y} f_{x}+\frac{r_{y}\left(p_{x}-x_{0}\right)^{2}}{f_{x}}$$

$\Delta p_{x}=p_{x}^{\prime}-p_{x}$，$\Delta p_{x}$就是监督信号的来源。

这里可以想象沿着y轴从上往下看相机坐标系，大概就是个二维坐标绕原点旋转的情形。

$p_{x}^{\prime}$就是u2，$p_{x}$就是u1。

后面的推导看的不是太懂，最后推导出了一个关于误差的不等式，应该符合什么样的规律，

也没说具体怎么操作，文章4.4节开头大概说了一下网络结构。

到了这里我就想：为什么我们不直接解方程组1来得到所有我们想要的 z,R,t,K，反正

所有的东西都是从方程组1来的，每一对像素都可以列一个方程。。。

 

文章里还说了，除了有移动物体的区域，整个图像上每个像素的 R 和 t 都是一样的。

用了一个mask来代表有移动物体的区域，在这个mask内的像素 t 可以不一样。

文章用了两个网络，

一个预测深度，

一个预测其他的东西（egomotion, object motion field relative to the scene, and camera intrinsics ) 

网络应该是把 有遮挡的区域 和 移动物体区域 一并处理了

可以猜测，学习内参K无非是在学习pose的基础上再多学几个参数，而且这些参数在

迭代过程中趋向于一个固定的值，文章中的说法是从 posenet 的bottleneck引出来的。

这样看来学习内参K似乎也没那么难。。。

 

 

要换掉batch normalization !

 

batchsize越大反而不好，把 batch normalization换成带有高斯噪声的layer nomalization

后效果会大大提高，之后增加batchsize才会略微让效果变好。。。

添加一定的噪声相当于正则化

另外一种理解是噪声能挤压解空间，缩小搜索范围，提高迭代效果。

我之前因为显存不足都是把batchsize设为1 然后训练一晚上，歪打正着。。。

 

2019年7月21日23:01:40

关于LayerNorm，pytorch 中已经有实现：

https://pytorch.org/docs/stable/nn.html?highlight=layernorm#torch.nn.LayerNorm 

另外如果要加噪声的话参考这个：

https://github.com/pytorch/pytorch/issues/1959  

直接在mean 和 std 上加噪声。

高斯噪声是噪声功率一定的情形下，对信号干扰最大的噪声类型。

另外一个博客：

https://zhuanlan.zhihu.com/p/69659844   

 

2019年7月25日14:50:59

折腾了两三天，写了好几个给 layernorm层 的 均值和方差 参数 加噪声的版本，pytorch自带的

layernorm并不能显式的、方便的把噪声加入，单这一项工作就可以写一篇博客了。。。

写了一个更完善的 data loader 。。。 

下面是最终写好的带噪声的layernorm层：

class LnWithGN_N2(nn.Module):
    '''
    对 NCHW 中的CHW做归一化，对于每个样本需要训练的参数就只有2个，因此
    N个样本就2N个待训练参数，初始化的时候要预先知道N，即batchsize
    '''
    def __init__(self, batchsize, eps=1e-5, affine=True):
        super(LnWithGN_N2, self).__init__()
        self.batchsize = batchsize
        self.affine = affine
        self.eps = eps

        if self.affine:
            self.gamma = nn.Parameter(torch.Tensor(self.batchsize).uniform_())
            self.beta = nn.Parameter(torch.zeros(self.batchsize))

    def forward(self, x):
        shape = [-1] + [1] * (x.dim() - 1)
        
        mean = x.view(x.size(0), -1).mean(1).view(*shape) 
        std = x.view(x.size(0), -1).std(1).view(*shape)
        
        # 这里随便加了5%幅值的噪声
        # torch.randn生成均值为0，方差为1 的高斯分布的数值。
        mean = mean + 0.05*torch.randn( mean.size() )*mean 
        std = std + 0.05*torch.randn( std.size() )*std
        
        mean = mean.expand( x.size() )
        std = std.expand( x.size() )

        y = (x - mean) / (std + self.eps)
        
        if self.affine: 
            shape = [self.batchsize] + [1] * (x.dim() - 1) # [N, 1, 1, 1]
            
            y = self.gamma.view(*shape).expand( x.size() )*y + \
                self.beta.view(*shape).expand( x.size() )
        return y

 

2019年8月3日23:39:36

遮挡部分的计算，自己瞎改还不如直接改geonet来的快，

把loss计算部分做针对性修改就好了。

geonet还把光流计算好了，对于预测移动区域的深度估计更方便。

github上只有一个看起来跑不起来的pytorch版geonet，呕。

讲到这里就会发现，在相邻帧中预测出的深度不一致，可以用来辅助提升

光流的计算效果。

 

上面的layernorm用了后反而效果有所下降。。。还要研究研究。。。

 

2019年8月18日15:25:42

youtube上有个台湾男生发布各种解说深度估计的论文的视频，搜monodepth2、struct2depth

就能搜到。

 

忽然想到，那个前车和本车速度一样，深度估计就会估计成无限远的问题的解决方法。

之前的做法都是互相warp到对方的位置，考察一致性。

解决无限远的问题，应该warp到一个固定的世界坐标系考察一致性。

 

上面提过

把$\mathbf{z}_{L}$变换(warp)到右相机所在的位置得到深度$z_{L}^{\prime}$

把$\mathbf{z}_{R}$变换到左相机所在的位置得到深度$z_{R}^{\prime}$ 

 

如果前车和本车运动速度一样，那么上述四个z都是一样的，永远都追不到的点

当然是无限远的点。

为了让warp后的距离不一样，那就应该warp到一个固定的坐标系计算距离，除了

target和source的坐标系外，还要引入另外一个不随着 target 和 source 运动的坐标系，

从固定坐标系来看，前车就是运动了。