历时4周,完成北航2022OO课程unit1,写此blog进行总结纪念。
一、基于度量来分析自己的程序结构
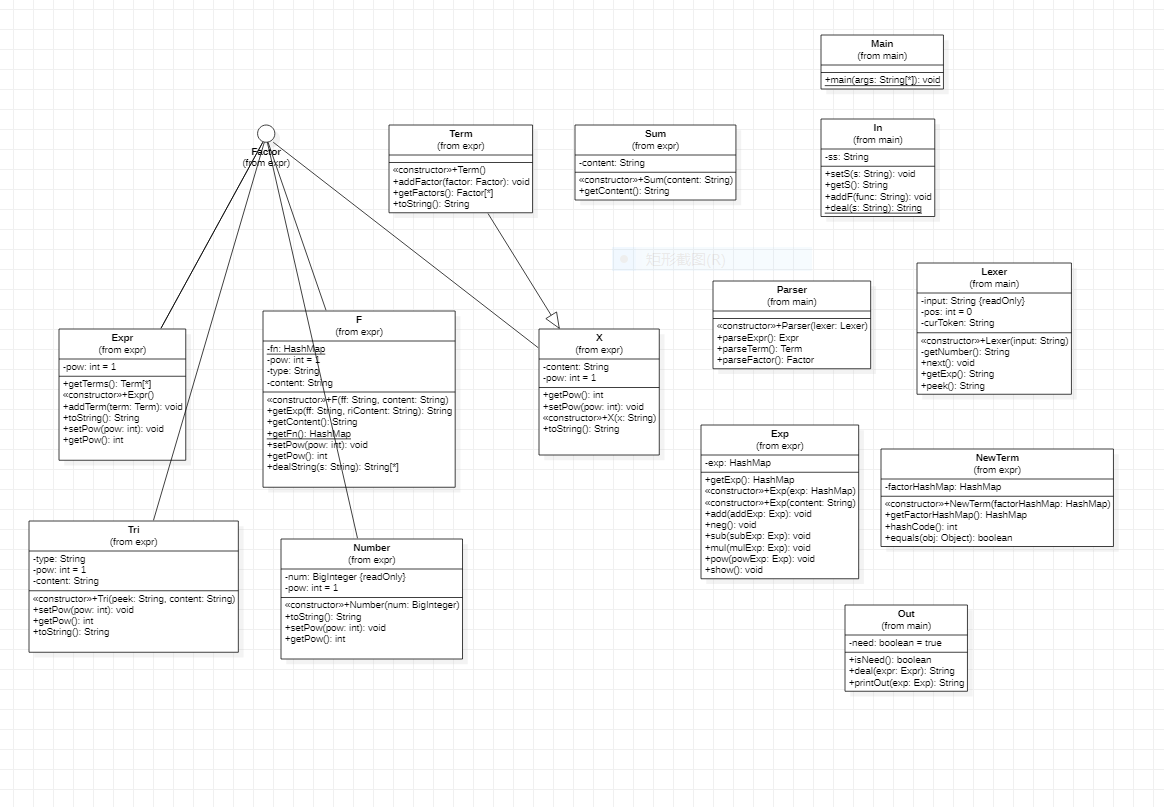
Main:
程序入口。在此进行各个类的聚合,最终得到结果。
In:
输入处理类。在此进行输入的字符串的预处理,包括最终表达式和函数定义。
Parser:
递归下降解析表达式。包括Expr和Term和Factor三个部分。与Lexer和Expr、Term等表达式相关类相互配合。
Lexer:
对表达式字符串进行遍历,根据要求返回数字、符号、表达式。
Factor(接口):
便于统一不同因子。
Term:
项类。用来表示单个项,并且有toString方法来将该项转化为后缀表达式。
Expr:
表达式类。并且有toString方法来将该表达式转化为后缀表达式。
F:
函数类。有getExp方法用来将实参代入形参,返回一个新的raw表达式。
X:
用来表示x和+、-、*等符号。后者实际上是没必要的。
Tri:
三角函数类。用来表示三角函数,有toString方法,返回一个处理好(即中缀表达)的表达式。
Number:
常数类。用来表示常数。
Sum:
求和类。用来直接处理sum(i,num1,num2,expr)的形式,并直接返回一个raw表达式。
Exp:
新的表达式类。有构造方法,配合NewTerm类将后缀表达式的运算数转化成一个Exp,即Hashmap<NewTerm, BigInteger>的形式。有add、neg、sub、mul、pow等运算。
NewTerm:
新的项类,由一个Hashmap<String,Integer>储存项和该项的指数。
Out:
计算类和输出类。在此进行后缀表达式计算的书写和结果的输出(稍微化简)。
以下是度量数据:
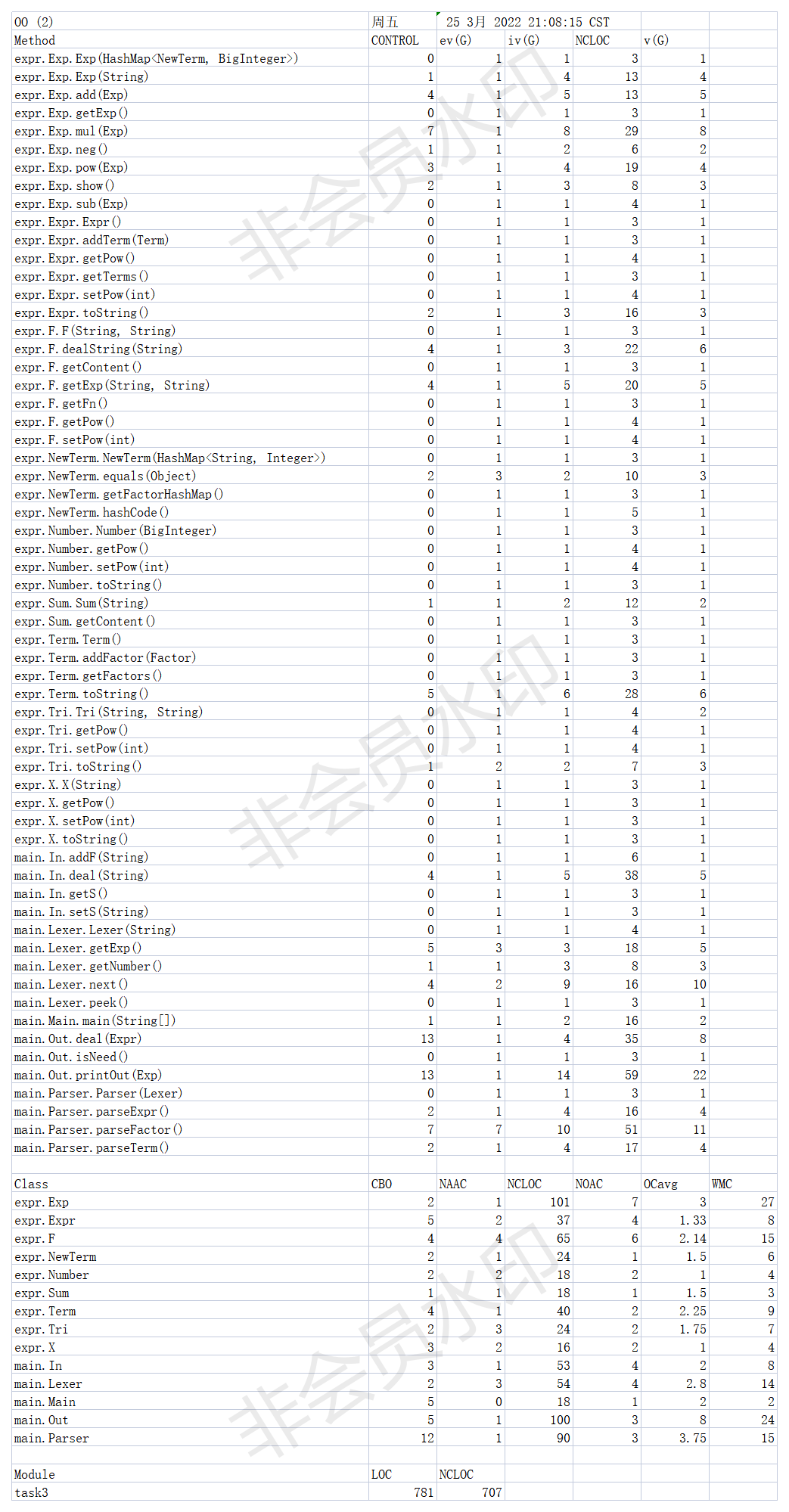
优点:
1、 高内聚低耦合的类设计。从CBO(coupling with objects)数据可以看出,每个类与其他类的联系基本在2-5之间,除了Parser这个需要与字符串表示类交互的类。类的耦合度较低。
2、结构清晰,流程分离。从UML图可以看出,作业大致分成两个部分,一个是表达式的表示部分,一个是表达式的处理部分,并且有独立的In、Out类。
3、大部分方法的设计较为良好。从方法的控制分支数目和ev、v、iv可以看出,大部分的方法的控制分支数目、基本复杂度、圈复杂度、结构复杂度都较低。
缺点:
1、 少数类的复杂度、耦合度较高。比如Parser、Out类。
2、 少数方法的复杂度较高。比如ParserFactor、Printout,Next方法。
3、 类的方法个数偏多,不够简练。
二、分析bug
task1:
未发现bug。
task2:
发现1个bug。
0 +(-sin(x)**3+x*sin(x))**+00
特征:(-sin) or (-cos),即左括号+负号+三角函数。
问题在于,在字符串预处理的时候,忘记处理此类情况,导致在Parser解析的时候,读完括号后将无法读取-sin。
问题所在类和方法: In.deal(String)。
对比和其他正常方法的代码行和圈复杂度的差异:代码行为38行,圈复杂度为5,在所有方法里基本是较高水平。
task3:
发现2个bug。
bug1:
0
(-+(+-((((((((((((((--(((((((((++ (((((x*(x-(x*(x-(x*(x-(x*((x+x*(1)))))))))))))))))))))))))))))))))))))))
特征:(-(-( , 即连续的左括号+负号。
问题在于,在字符串预处理的时候,用正则的replaceall方法对出现 (-(的情况进行替换,替换为(-1*(, 然而在该样例中,替换完第一个(-(后,指针已经指向了第二个负号,从而漏掉了第二个左括号,导致Parser解析失败。
问题所在类和方法: In.deal(String)。
对比和其他正常方法的代码行和圈复杂度的差异:代码行为38行,圈复杂度为5,在所有方法里基本是较高水平。
bug2:
1
f(x,y)=(((sin(cos(x))-(+1-sin(cos(y))))))
(f(f(x,x**1),x**+1)*cos(x)**+01)-(cos(sin((x**2))))-(+098782738)**+03
特征:自定义函数的调用的实参为具有多个实参的自定义函数。
问题在于,在进行实参代形参的处理时,一致以逗号分割实参,导致实参分割错误,进而替换失败。
问题所在类和方法: F.getExp()。
对比和其他正常方法的代码行和圈复杂度的差异:代码行为20行,圈复杂度为5,在所有方法里处于中等水平。
三、分析自己发现别人程序bug所采用的策略
测试策略:基于不同模块采取独立测试,并进行整合。
以第三次作业为例,该次作业的表达式由三角函数、sum、F、x、括号嵌套组成。所以可以先对三角函数进行测试,即根据三角函数的形式化表达构造完整的样例,基本覆盖所有可能出现的情况。对于sum、F等同理。
最终,再整合到一起构造样例进行测试。如此,由易到难、从简入深,可以较为系统的进行debug。
有效性:在task3中,hack成功8次。
四、架构设计体验
task1:
最开始的时候,由于没什么思路,并且其他任务较多,便选择了预解析的处理方式,2h写完,因为预解析相当于做完了一半甚至更多的工作,剩下的只是选取适合的数据结构进行表达式的储存和计算,计算的过程中其实相当于化简。
此处数据结构选择HashMap<Integer, BigInteger> exp,key为x的次数,value为该项的系数,计算的过程可以理解在同时化简,即加法运算时若次数相同,则系数相加,减法同理,乘法运算时,次数相加、系数相乘,乘方则化为乘法。
但与其他同学交流后,发现训练的作业有递归下降的比较完备的演示,于是抱着试试看的态度用递归下降对raw表达式进行处理,发现效果很好,于是用递归下降化为类似预解析的后缀表达式,然后直接套上之前写的计算。在递归下降的处理
过程中,有如下细节:
1. 字符串预处理
将空格tab去掉,将连续的+-号化成只有一个+号 or -号。
对开头的-号、(-、*-进行特殊处理。
2. 解析的形式
没有采纳指导书将减法运算变为加法运算的建议,而采用了减法运算。
没有进行neg运算,因为字符串预处理的时候将neg运算变为了-1*运算,比如-x,变为-1*x,-1是一个整体。
对指数的处理,则是在可能出现指数的类(X,Expr)增加pow属性,乘法运算也是运算的一种。
以上细节也为之后task2、3的迭代埋下了伏笔。
架构上,没有采取单独输入输出类的形式,使得类较为复杂,耦合性高。
task2:
此次作业迭代较多,增加了三角函数、自定义函数、求和函数3种因子。
由于懒,并且觉得后缀表达式的形式还可以对递归下降的表达式结果进行初步检验,便沿用task1的计算方法,没有采取边解析边计算的方法。
至于本次处理字符串,对于自定义函数和求和函数,本质上其实是替换,所以新增两个类,在F和sum类里面进行因子和i的替换,最终返回表达式因子。
对于三角函数,本次处理目光较为短浅,单单考虑了task2的要求,所以用Term来读取三角函数括号里的字符串,最终返回一个sin(string)类因子。
task3:
相较于1to2的迭代,本次迭代较为简单,增加了多层括号嵌套,以及三角函数、自定义函数、求和函数的因子复杂化。
对于前者,递归下降的架构已经解决。求和函数本质上是一个表达式,所以解决其他问题也就解决了该问题,不用考虑。
三角函数因子复杂化,考虑用Expr代替Term进行括号内因子的读取,并直接转化为中缀形式的String,之后同task2。
自定义函数因子复杂化,主要体现在可以出现sum和自定义函数的调用,虽然本质上也是表达式问题,但要注意之前处理方式是否能够沿用。事实证明,不能再用简单的逗号分割实参。所以写了个字符串处理函数处理。
task1-3总结:
最初的架构会影响到之后的所有架构。所以在设计时,就要考虑之后可能实现的方式,尽量在可拓展性和复杂性之间做个平衡。
个人认为本次作业的最优解应是如下:
在字符串处理方面,进行预处理,变sub、neg运算为 +-1*、-1* 运算,即首先化为单+ or 单负,之后再变-为+-,变-为-1*,如此,则取消了sub运算和neg运算。之后进行递归下降。
在计算方面,采用边解析边运算的方式,一步到位,省时省力。
五、心得体会
算上这次博客,我与OO已经度过了4周的时间,做了3次迭代式的作业和1次博客。获得了成长,也有许多感悟。
1. 写代码就是在不断的权衡取舍,我们要做的不是追求省事,而是尽量做出一个完美的版本。
所谓权衡取舍,体现在很多方面。这次作业的整体架构、采用预解析还是normal、要不要重构、选择追求性能分还是确保不出错……这些都是我反复思考的问题,没有绝对的对错。但我认为,我们仍应尽可能地追求
一份比较完美的代码,追求赏心悦目,追求不断优化。能力,就是在这样一次次突破中突破的。
2. Bug是我们成长的动力,去发现它、解决它、认识它。
发现bug,考验我们的样例构造水准,更深层次讲其实是认识问题的深度和思维的缜密度。
解决bug,考验我们的代码水平,如何高效地解决此bug并且不新增bug。
认识bug,考验我们的反思能力,为什么会出现这样一个bug?是代码的疏忽还是架构的缺漏?如何避免它?
3. 写代码,写得越多,你就越强!
这个观点很绝对,是的,这个观点很绝,但就是对的。
代码量1万行跟10万行的程序员,绝对有着质的差别。写多了,其实就是见的世面广了,认识的bug多了,知道的库多了,知道的解决方法多了。所以,你码代码的速度不仅更快,而且码的代码一看,就有高手的风范。
4. OO的思想,以对象为单位。
所谓对象,其实就是一个个类。通过类与类的高内聚低耦合的交互,解决问题。
5. 迭代式的开发,要持续log跟进记录。
log记录迭代增量和减量,便于迭代开发中的回溯和进一步迭代,也便于复盘。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号