推荐系统排序（Ranking）评价指标
一、准确率（Precision）和召回率（Recall）
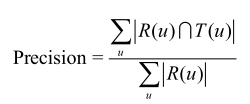
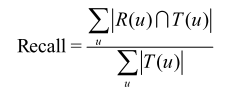
准确率和召回率计算方法的Python代码如下：
def Recall(train,test,N): hit=0 all=0 for user in train.keys(): Tu=test[user] rank=GetRecommendation(user,N) for item,pui in rank: if item in Tu: hit+=1 all+=len(Tu) return hit/(all*1.0) def Precision(train,test,N): hit=0 all=0 for user in train.keys(): Tu=test[user] rank=GetRecommendation(user,N) for item,pui in rank: if item in Tu: hit+=1 all+=N return hit/(all*1.0)
下面的Python代码同时计算出了一个推荐算法的准确率和召回率：
def PrecisionRecall(test, N): hit = 0 n_recall = 0 n_precision = 0 for user, items in test.items(): rank = Recommend(user, N) hit += len(rank & items) n_recall += len(items) n_precision += N return [hit / (1.0 * n_recall), hit / (1.0 * n_precision)]
有的时候，为了全面评测TopN推荐的准确率和召回率，一般会选取不同的推荐列表长度N，计算出一组准确率/召回率，然后画出准确率/召回率曲线（precision/recall curve）。
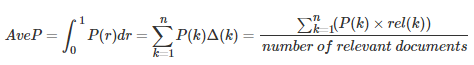
其中rel(k)表示第k个文档是否相关，若相关则为1，否则为0，P(k)表示前k个文档的准确率。 AveP的计算方式可以简单的认为是：
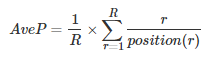
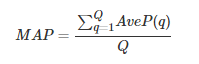
- 单个主题的平均准确率是每篇相关文档检索出后的准确率的平均值。
- 主集合的平均准确率(MAP)是每个主题的平均准确率的平均值。
- MAP 是反映系统在全部相关文档上性能的单值指标。系统检索出来的相关文档越靠前(rank 越高)，MAP就应该越高。如果系统没有返回相关文档，则准确率默认为0。
- MAP的衡量标准比较单一，q(query，搜索词)与d(doc，检索到的doc)的关系非0即1，核心是利用q对应的相关的d出现的位置来进行排序算法准确性的评估。
- 需要注意：在利用MAP的评估的时候，需要知道：1. 每个q有多少个相关的d; 2. 排序结果中这些d的位置 3. 相关的定义
（1）Cumulative Gain(CG)：
表示前p个位置累计得到的效益，公式如下：
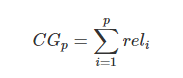
其中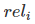 
表示第i个文档的相关度等级，如：2表示非常相关，1表示相关，0表示无关，-1表示垃圾文件。
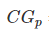的计算中对位置信息不敏感，比如检索到了三个文档相关度依次是{3,-1,1}和{-1,1,3}，显然前面的排序更优，但是它们的CG相同，所以要引入对位置信息的度量计算，既要考虑文档的相关度等级，也要考虑它所在的位置信息。假设每个位置按照从小到大的排序，它们的价值依次递减，如：可以假设第i个位置的价值是
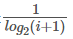，那么排在第i个位置的文档所产生的效益就是
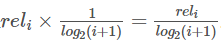。公式如下：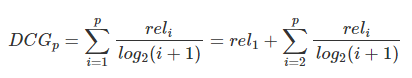 
另一种比较常用的，用来增加相关度影响比重的DCG计算方式是：
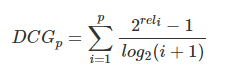
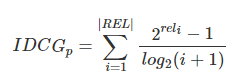
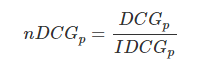
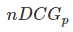就是从0到1，不同查询语句之间就可以做比较，就可以求多个查询语句的平均
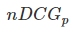。 reciprocal rank是指，第一个正确答案的排名的倒数。MRR是指多个查询语句的排名倒数的均值。公式如下：
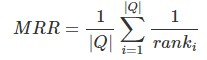
其中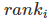
表示第i个查询语句的第一个正确答案的排名。
MRR是一个国际上通用的对搜索算法进行评价的机制，其评估假设是基于唯一的一个相关结果，即第一个结果匹配，分数为 1 ，第二个匹配分数为 0.5，第 n 个匹配分数为 1/n，如果没有匹配的句子分数为0。最终的分数为所有得分之和。
这个是最简单的一个，因为它的评估假设是基于唯一的一个相关结果，如q1的最相关是排在第3位，q2的最相关是在第4位，那么MRR=(1/3+1/4)/2，MRR方法主要用于寻址类检索（Navigational Search）或问答类检索（Question Answering）。
MRR(Mean Reciprocal Rank)：是把标准答案在被评价系统给出结果中的排序取倒数作为它的准确度，再对所有的问题取平均。
有3个query如下图所示：（其中黑体为返回结果中最匹配的一项）
可计算这个系统的MRR值为：(1/3 + 1/2 + 1)/3 = 11/18=0.61。
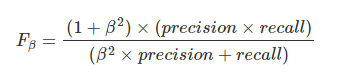
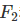和
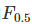，前者中recall重要程度是precision的两倍，后者则相反，precision重要程度是recall的两倍。matlab下 ROC和AUC的实现：
function [result]=AUC(test_targets,output) %计算AUC值,test_targets为原始样本标签,output为分类器得到的判为正类的概率，两者的维度（长度）要一样 % 均为行或列向量 [A,I]=sort(output); % sort 默认升序，而这里I 是output原来的索引 M=0;N=0; for i=1:length(output) if(test_targets(i)==1) M=M+1;%正类样本数 else N=N+1; %负类样本数 end end sigma=0; for i=M+N:-1:1 if(test_targets(I(i))==1) sigma=sigma+i; %（真实的）正类样本的rank相加，（概率大的rank高。 end end result=(sigma-(M+1)*M/2)/(M*N);
计算方法和例子详见：【Reference-4】
应用：
假设M有两个，N有两个。
那么原样本标签为：test_targets=[0, 0, 1, 1]。output =[0.3, 0.1, 0.4, 0.2]（概率，算出来的得分）。则 I 即为：[2, 4, 1, 3]
通过第一个for循环，算出M，N的值后。（不难理解）
在第二个for 循环：
for i=M+N:-1:1
if(test_targets(I(i))==1)
sigma=sigma+i; %（真实的）正类样本的rank相加
end
end
循环条件从 M+N递减到1，步长为1（-1）
先对 I(i) 取索引，I 是已经排好序的，从小到大的概率对应的Item 原先的位置。 I 即为：[2, 4, 1, 3]
for 循环，i 从4开始，I (4) 对应的是索引为3的item，则 test_targets(3) = 1 ，是==1 没错，那么sigma就 +4；
posted on 2018-07-14 15:19 CuriousZero 阅读(43447) 评论(3) 编辑 收藏 举报
