『数据结构』RMQ问题
RMQ(Range Minimum/Maximum Query),即区间最值问题。
对于长度为 n 的数列 A ,回答若干查询 RMQ(A,i,j)(i,j<=n) ,返回数列 A 中下标在 i,j 里的最大(小)值。
相关算法
- 朴素(搜索),时间复杂度:\(O(n)-O(q \times n)\) ,在线;
- 线段树,时间复杂度:$O(n)-O(q\times logn) $,在线;
ST(动态规划),时间复杂度:\(O(n\times logn)-O(q)\),在线;RMQ标准算法,先规约为LCA,再规约成约束RMQ,时间复杂度:\(O(n)-O(q)\),在线。
ST 算法
假设当前题目要求区间最小值,我们令 dp[i][j] 代表从 i 开始,长度为\(2^{j}\)这段区间的最小值。
于是便有:\(dp[i][j]=min(dp[i][j-1],dp[i+^{j-1}][j-1])\)
分析可知,\(dp[i][j-1]\)代表从 i 开始,长度为\(2^{j}\)区间一半中的最小值,而 \(dp[i+2^{j-1}][j-1]\)即为区间的另一半。
即为区间的另一半。
最终(从下往上看):
| \(dp[0][*]\) | \(dp[1][*]\) | \(dp[2][*]\) | \(dp[3][*]\) | \(dp[4][*]\) | \(dp[5][*]\) | \(dp[6][*]\) | \(dp[7][*]\) | |
|---|---|---|---|---|---|---|---|---|
| \(dp[*\)][3] | \(1\) | |||||||
| \(dp[*\)][2] | \(1\) | \(1\) | \(1\) | \(5\) | \(2\) | |||
| \(dp[*][1]\) | \(3\) | \(1\) | \(1\) | \(5\) | \(7\) | \(6\) | \(2\) | |
| \(dp[*][0]\) | \(4\) | \(3\) | \(1\) | \(5\) | \(7\) | \(8\) | \(6\) | \(2\) |
预处理
根据状态转移方程,首先指定当区间长度为\(2^{0}\)时的各初始值,随后推出后面的结果。
void ST_Init(const vector<int> &A) {
int n=A.size();
for (int i=0; i<n; i++)
dp[i][0]=A[i];
for (int j=1; (1<<j)<=n; j++)
for (int i=0; i+(1<<j)<=n; i++)
dp[i][j]=min(dp[i][j-1], dp[i+(1<<(j-1))][j-1]);
}
查询
预处理出整个 dp 数组以后,查询操作很简单,令 k 为满足\(2^{k} \leq R-L+1\)的最大整数,则以 L 开头、以 R 结尾的两个长度为\(2^{k}\)的区间合起来即覆盖了查询区间 [L,R] 。
int RMQ(int L, int R) {
int k=0;
while ((1<<(k+1))<=R-L+1) k++;
return min(dp[L][k], dp[R-(1<<k)+1][k]);
}
嗯!怎么说呢?感觉线段树在这种类型的题目中好像是最万能的方法了。
无论是 [点修改+查询] 还是 [区间修改+查询] ,它都可以做到 \(O(logn)\)的复杂度,而且在线段树中我们也可以维护好多东西(区间和、最值等等)。
对于一维中的线段树,我们想要查询某个区间的最值,首先就应该建树咯~(具体方法省略)
而在查询时,我们可以从根节点向下递归搜索,如下图,假设查询区间为 [2,6] 。
将 [2,6] 这一个大区间分解为不相交的三个小区间 [2,3]、[4,5]、[6] ,而最终的结果便由这三个节点中所维护的信息决定的!
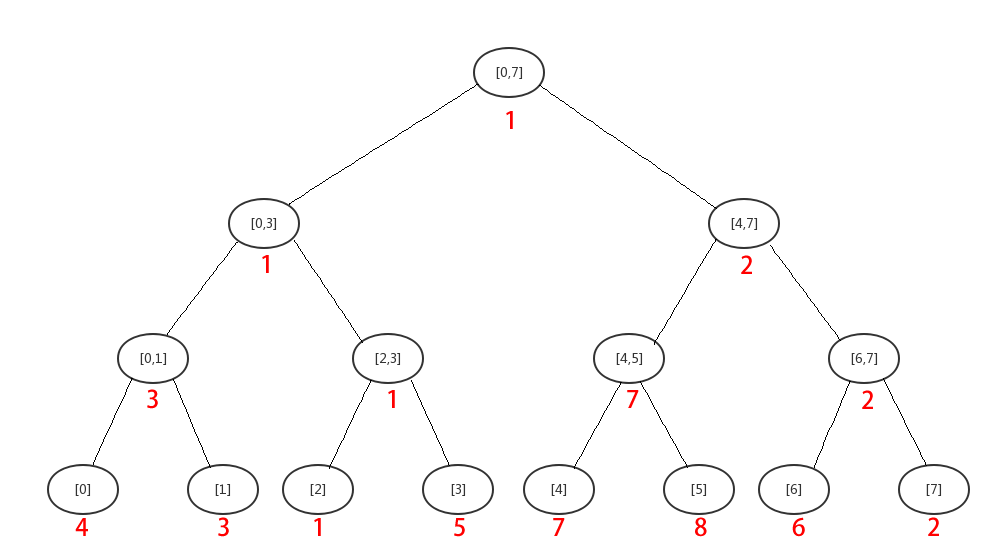
我们假设查询还是区间最小值,于是最终的结果为\(\min(1,7,6)=1\)
线段树可以解决普通的 [点/区间] 修改+查询 ,当然它也可以解决 树中的路径权值 修改+查询(树链剖分)。


【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步