tarjan 强连通分量

tarjan 强连通分量

一、强连通分量定义

有向图强连通分量在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)SCC。

以上是摘自百科的一段对有向图强连通图分量的形式化定义。其实不难理解，举个例子

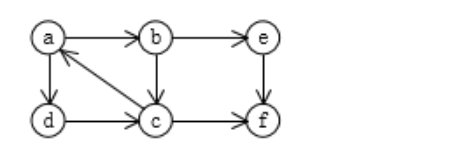
如上图，{a,b,c,d}为一个强连通分量，{e}为一个强连通分量，{f}为一个强连通分量。

三、dfs相关概念

tarjan算法本身是一个dfs算法，用到了dfs的一些性质,所以具体展开tarjan SCC算法之前，先来梳理一些相关的基础。

1、搜索树（森林）：对一个图做dfs搜索，搜索过程形成一颗搜索树。
2、节点访问次序d[i]: dfs过程中，按照节点访问到的顺序个每个节点记录一个值d[i]。另外，也可以对每个节点记录访问完成的次序f[i]。

3、dfs对边的分类：

　　树边：搜索过程中自然形成的边。如果通过节点i dfs搜索其邻居节点j时，发现j之前还未被访问，在dfs搜索j，这时边<i,j>形成搜索树种一条搜索经过的边，称作树边

   反向边：搜索过程中后裔指向祖先的边。如果通过节点i dfs搜索其邻居节点j时，发现j在搜索树中是i的祖先（j已经被dfs搜索到，但是还没递归返回），这时边<i,j>是反向边。

　　正向边：搜索过程中祖先指向后裔的边。

　　交叉表：搜索过程中不同子树之间的边。