LeetCode第31题："下一个排列" C#篇

理解题意：

 这道题大概的意思是，将nums数组换一个排列方式，但要求比当前排列要大并且是当前数组大的排列中最小的一种排列

思路：

相信很多人看到这题第一个会想到的思路是，我只需要将这个数组所有比当前数组大的排列都整理出来，再选出最小的那一个排列，此题可解

很显然啊....这不是一个标准的答案，这个思路的时间复杂度是O(n!) 也就是n的阶乘,拿示例1举例n=3那么就是1*2*3=6,假设n=100或者1000或者更高 所以....嗯....额你懂的对吧

 我们应该可以把这个时间复杂度优化到O（N）,请各位观察下这两组数字

54321（排列前）

12345（排列后）

从上面数字中，我们看到单调递减的数字是无法得到这个解的，题目中的示例2也是如此，由此推测，正确答案是不是和单调递减有关系呢？

请再看下面这个示例

24534421（排列前）

 24541234（排列后）

会发现我们从右往前数,我找到那位破坏单调递增的数字，再找到比这个数字大中最小的那个数字（注意是要靠后），交换位置，并将后面的数字升序排序即可

这里解释一下，为什么要从右往前数，因为调换越后面的数字，整个排列变化的值越小，这样是离正确答案最近的一条选项，请看下面例子

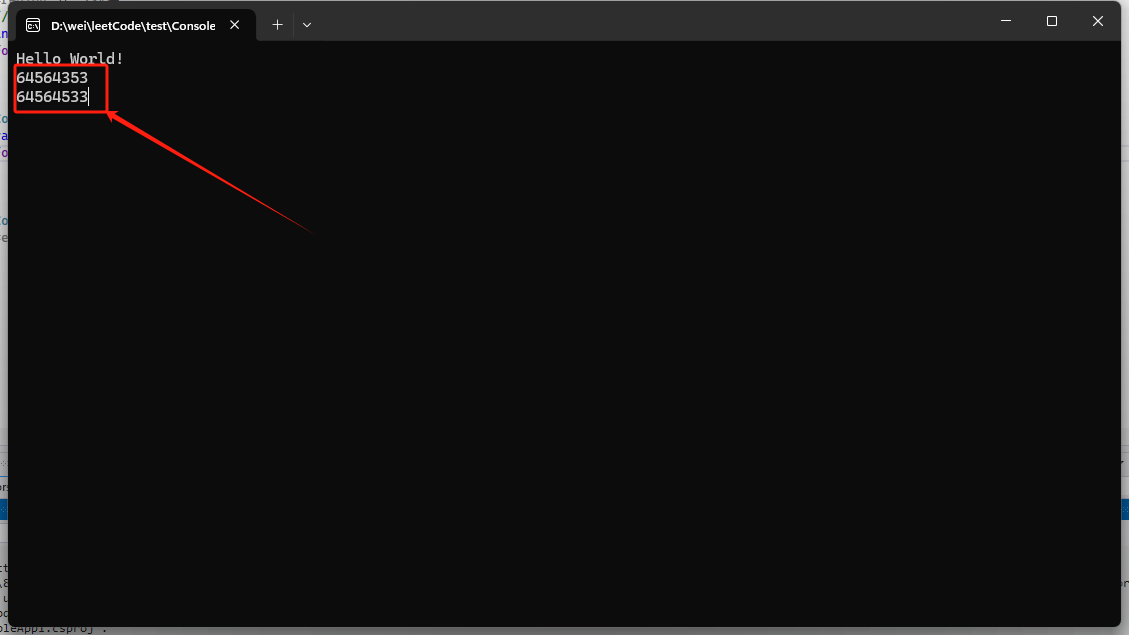
64564353（排列前）

64564533（排列后）

总结一下逻辑思路：

首先，需对输入数组进行初步判断，以确定其是否存在多种排列可能。对于仅包含单个元素的数组，例如 nums = {1}，由于其排列方式唯一，不存在 “下一个排列” 的概念，故直接返回该数组。

接下来，在数组中从右往左进行扫描，目的是定位首个破坏单调递增序列特性的数字。若整个数组呈现单调递减的态势，意味着它已是所有可能排列中的最大排列，不存在字典序更大的下一个排列。此时，直接将数组反转并返回，这样得到的便是字典序最小的排列，符合逻辑要求。

在找到上述破坏单调递增的数字后，继续从右往左遍历数组，以确定比该数字大且在所有大于它的数字中值最小的那个数字，并交换这两个数字的位置。

最后，将交换位置后该数字后面的所有数字进行升序排序，从而完成 “下一个排列” 的构建操作，得到在字典序上紧跟原数组的下一个排列结果。

代码：

 /// <summary>
 /// 下一个排列
 /// </summary>
 /// <param name="nums"></param>
 /// <returns></returns>
 public static int[] NextArrangement(int[] nums)
 {
     //如果数组为空或只有一个元素，则无法进行下一个排列
     int len = nums.Length;
     if (len==1)
     {
         return nums;
     }

     //从右向左找到第一个降序的元素
     int i = len - 2;
     while (i >= 0 && nums[i] >= nums[i + 1])
     {
         i--;
     }

     //如果数组已经是降序排列，则无法进行下一个排列
     if (i<0) 
     {
         reverse(nums, 0, len - 1);
         return nums;
     }

     //从右向左找到第一个大于nums[i]的元素
     int nextGreaterIndex = i + 1;
     while (nextGreaterIndex < len && nums[nextGreaterIndex] >nums[i])
     {
         nextGreaterIndex++;
     }
     
     //交换nums[i]和nums[nextGreaterIndex-1]
     swap(nums, i, nextGreaterIndex - 1);
     //将nums[i+1]到nums[len-1]进行反转
     reverse(nums, i + 1, len - 1);
     return nums;
 }

 /// <summary>
 /// 交换数组中的两个元素
 /// </summary>
 /// <param name="nums"></param>
 /// <param name="i">开始下标</param>
 /// <param name="j">结束下标</param>
 private static void swap(int[] nums, int i, int j)
 {
     int temp = nums[i];
     nums[i] = nums[j];
     nums[j] = temp;
 }

 /// <summary>
 /// 反转数组中的元素
 /// </summary>
 /// <param name="nums">数组</param>
 /// <param name="start">开始下标</param>
 /// <param name="end">结束下标</param>
 public static void reverse(int[] nums, int start, int end)
 {
     while (start < end)
     {
         swap(nums, start++, end--);
     }
 }

使用：

#region 下一个排序
//int[] nums = new int[] { 2, 4, 5, 3, 4, 4, 2, 1 };
int[] nums = new int[] { 6, 4, 5, 6, 4, 3, 5, 3 };
for (int i = 0; i < nums.Length; i++)
{
    Console.Write(nums[i]);
}
Console.WriteLine("");
var result=Calculation.NextArrangement(nums);
for (int i = 0; i < result.Length; i++) 
{
    Console.Write(result[i]);
}
Console.Read();
#endregion

结果：

时间复杂度优化解析:

整体代码实现 “下一个排列” 功能的思路是这样的：首先从右往左去查找破坏了升序的那个元素，此过程实际上是遍历数组元素，时间复杂度为线性的，也就是 O(n)，这里的 n指的是整个数组nums的长度。当找到这个破坏升序的元素后，接着要从右往左去寻找一个比它大的元素与之交换位置，这个寻找并交换的操作同样是在遍历数组元素，其时间复杂度也是O(n)。

 

完成交换操作后，对于该破坏升序元素后面的那部分元素，原本如果采用常规的排序算法，比如归并排序或者快速排序（平均情况），它们的时间复杂度会是 O(klogk)，这里的 k;表示的是破坏升序那个元素后面元素的长度；要是使用冒泡排序这类简单排序算法，时间复杂度则为 O(k²)。不过，在当前的实现中，我们并没有采用这些排序算法，而是直接通过反转这部分元素来达到调整顺序的目的，而反转元素的操作只需遍历一遍这部分元素即可，其时间复杂度为 O(k)。

 

综合来看，前面查找破坏升序元素以及寻找交换元素等操作的时间复杂度都是基于 O(n)的，而后续处理破坏升序元素后面部分元素的反转操作时间复杂度为O(k)，由于k是小于等于n的（k代表数组后半部分元素长度），在渐进分析中，整个算法的时间复杂度主要取决于前面O(n)的部分，所以最终整个代码实现 下一个排列功能的时间复杂度为O(n）。

结尾：

希望此篇文章对你有帮助，有更有的方法或者不太清楚有疑惑的地方也非常欢迎留言私信，当然啦，如果可以给威某人点一个小小的赞就更好啦哈哈 ，下篇再见，各位家人~