博弈论 随记
博弈论
1. 简单博弈
正推/反推。纸上画画直观图(ven图,条形图等),找必胜区间和必败区间。一般此类问题都有同余的必胜点。
2. Nim游戏
有若干堆石子,每堆石子的数量ai都是有限的,合法的移动是“选择一堆石子并拿走若干颗(不能不拿)”,如果轮到某个人时所有的石子堆都已经被拿空了,则判负(因为他此刻没有任何合法的移动)。
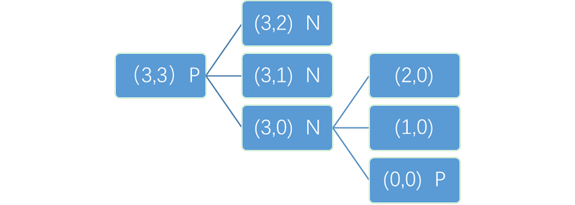
※对于(a1,a2,a3,…an)局面: a1^a2^...^an==0 (^为异或) ![]() 为P-position,先手必败/**/
为P-position,先手必败/**/
{/*
对N/P状态的理解:N-position (Now,当前状态)现在轮到move的人有必胜策略的局面。
P-position(Previous,上次状态) 上一次move的人有必胜策略的局面。
若A局面的子局面a[i]中存在P,则A为N。
若A局面的子局面a[i]全部为N,则A为P。
递归,子状态推出开始局面(3,3)的N/P。
用DP或者记忆化搜索降低时间复杂度。
*/}
3. SG函数
例1.n堆石子,每次可以从第1堆石子里取1颗、2颗或3颗,可以从第2堆石子里取奇数颗,可以从第3堆及以后石子里取任意颗……
先看例2.一个有向无环图和一个起始顶点上的一枚棋子,两名选手交替的将这枚棋子沿有向边进行移动,无法移动者判负。事实上,这个游戏可以认为是所有Impartial Combinatorial Games的抽象模型。
首先定义mex(minimal excludant)运算,这是施加于一个集合的运算,表示最小的不属于这个集合的非负整数。例如mex{0,1,2,4}=3、mex{2,3,5}=0、mex{}=0。
对于一个给定的有向无环图,定义关于图的每个顶点的Sprague-Grundy函数g如下:g(x)=mex{ g(y) | y是x的后继 }。g(x)含义不理解先看SG函数的性质。
SG函数的性质:所有的terminal position所对应的顶点,也就是没有出边的顶点,其SG值为0,因为它的后继集合是空集。然后对于一个g(x)=0的顶点x,它的所有前驱y都满足 g(y)!=0。对于一个g(x)!=0的顶点,必定存在一个后继y满足g(y)=0。
顶点x所代表的postion是P-position当且仅当g(x)=0(跟P/-position的 定义的那三句话是完全对应的)。我们通过计算有向无环图的每个顶点的SG值,就可以对每种局面找到必胜策略了。
当g(x)=k时,表明对于任意一个0<=i<k,都存在x的一个后继y满足g(y)=i。也 就是说,当某枚棋子的SG值是k时,我们可以把它变成0、变成1、……、变成k-1,但绝对不能保持k不变。不知道你能不能根据这个联想到Nim游戏, Nim游戏的规则就是:每次选择一堆数量为k的石子,可以把它变成0、变成1、……、变成k-1,但绝对不能保持k不变。这表明,如果将n枚棋子所在的顶点的SG值看作n堆相应数量的石子,那么这个Nim游戏的每个必胜策略都对应于原来这n枚棋子的必胜策略!