多元统计分析-概率,期望,方差,正态分布
概率,期望,方差
只有一个变量时
F(x<=a) = ∫-∞af(x)dx
当区间取负无穷到正无穷时积分为1
推广到多元之后:

同理,当区间取满整个空间时,积分为1
f被称为概率密度函数
边缘分布函数
当多元函数的n-m个变量取负无穷到正无穷之后
概率函数变为有m个自变量的函数(一共有n个自变量)
此时的概率密度函数被称为这m个自变量的边缘密度函数
若n个自变量相互独立,则每个自变量边缘密度函数的乘积为联合分布的概率密度
均值与方差:
均值一元时相同,只不过是在每一位上求均值并最终将他们组合成一个向量
均值组合成的向量最为均值
同理,均值有如下特征
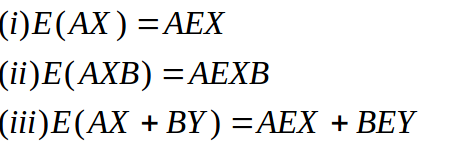
这里的A,B为矩阵,X为向量
由均值得出方差
D(X) = E(X-E(X))*(X - E(X))
D(x) = E(XX') - E(X)*E(X')
可以看到,协差阵是平方的期望,所以协差阵肯定是半正定的
这个正好是当X=Y时的协差阵
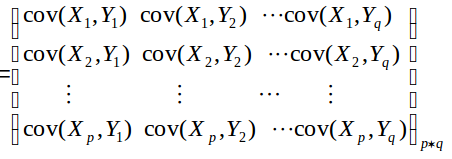
协差阵,相关系数阵,标准离差阵
当判断两个多元向量关系的时候,可先求出协差阵
协差阵的每个元素/这两个单独拿出来算的方差即可得到相关系数阵

正态分布:
密度函数:
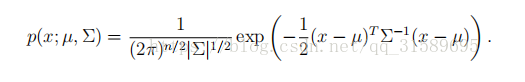
u:均值向量,∑协方差矩阵
由于协差阵半正定 当∑ = 0时特殊情况特殊考虑
n元正态分布的每一维都服从正态分布
若X服从N(u , Σ)
现在做变换 X‘ = AX + d
那么X’服从 N(Au + d, AΣA')



