直方图均衡

图像的灰度直方图

一幅图像由不同灰度值的像素组成，图像中灰度的分布情况是该图像的一个重要特征。图像的灰度直方图就描述了图像中灰度分布情况，能够很直观的展示出图像中各个灰度级所占的多少。
图像的灰度直方图是灰度级的函数，描述的是图像中具有该灰度级的像素的个数：其中，横坐标是灰度级，纵坐标是该灰度级出现的频率。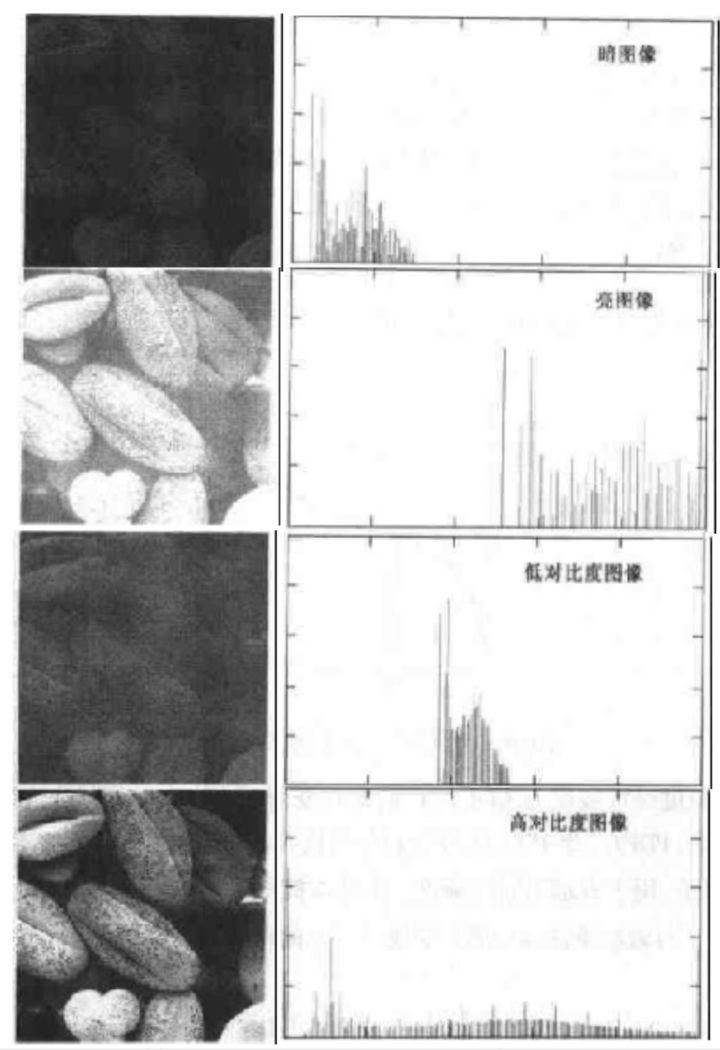

 

对于图片，可能大部分像素的灰度分布在某一个小区间上

这样的话会导致图像不清楚，如下:

那么直方图均衡化就是通过某种变化将像素密度均匀的分布到各个灰度区间，从而增加对比度

 

具体做法:

　　直方图均衡的本质是做灰度映射

　　设均衡前的图像为A， 均衡后的图像为B

　　图像A中的灰度为x通过直方图均衡函数f后，灰度变为y

　　这就是直方图均衡了，那么关键就是均衡函数怎么求了

 

均衡函数:

　　均衡函数必须单调递增(要不然均衡后的图片一下暗一下亮，那岂不是乱套了)

　　均衡函数必须是函数(必须要一一对应)

　　均衡后图像的直方图与均衡前在灰度上的积分要相等 (积分代表了像素的个数嘛，这玩意不能变的)

 

求法:

　　先将图像A的直方图做归一化，将灰度级归一化到0-1区间之内 (归一化方法可以是直接除以灰度的最大值)

　　将灰度归一化到0-1区间之后，我们可将灰度视为随机变量那么通过A的灰度直方图，我们可以得到直方图的密度函数p(x)

　　我们的灰度映射函数为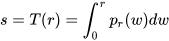

　　对于离散情况，我们使用如下方法

　　

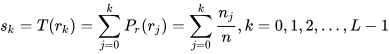
　　可以看到，不管是值域还是定义域都是[0,1]

　　然后可以理论证明这是均匀分布的

　　我们的直方图均衡就做完了