实变函数-集合与点集

集合

递减集合列

递增集合列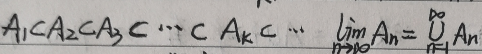

 上极限集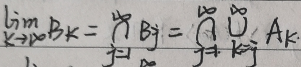

 

下极限集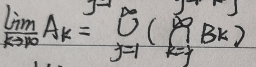

 

集合语言的相互转化

任意: 交集

存在：并集

映射

单射：

一对一

 

满射：

每个元素都有对应的像

 

对等：

若存在一个A->B的映射，可以把A，B中所有的元素一一联系起来，则称为A~B（A,B对等）

证明集合对等:

若X与Y的某个真子集对等，Y与X的某个真子集对等则X～Y

 

基数：

若A~B则A和B基数相等，自然数集的基数为N₀，(0,1]的基数为N₁记为c=2^N₀

一些常见的对偶集:

N~{y:y=2n}   y = 2*x

N*N~N    f(i,j) = 2^i-1(2*j - 1)

N~Z

 

可列集：

自然数集的基数为N₀，与自然数集对等的集合称作可列集

在众多的无限集中，最小的基数是N₀

 

可数集：

可列集和有限集统称可数集

 

集合在映射下的分解：

对于集合X，Y

X = x1∪x2

Y = y1∪y2

若存在单射f X->Y, g Y->X

则有f(x1) = y1 g(y2) = x2

 

点集的直径:diam(E) = sup(|x-y|),若diam(E) <正无穷，则称为有界集，

极限点：对于集合E，若存在E中的互异点列{x_k}若lim _k->∞ |x_k - x| = 0,x是E中的极限点，极限点集一般写为E'

孤立点：若x属于E，且x不是E中的极限点，则x为E的孤立点

R_n中任意有界无限集至少有一个孤立点

闭集：设E⊂Rⁿ 且E包含E中的所有极限点，则称为闭集

有限个闭集的并任是闭集

闭集族的交集为闭集

 

闭集套定理

若集列F为飞空有界，单调递减的闭集列

那么他的下极限不为空集