机器学习复习
1.判断与名称解释题
a
1.1 数据挖掘:在较大数据集上通过某些方式发现模型的一个过程
1.2 机器学习:研究如何通过计算手段,利用经验提升系统的性能
1.3 假设空间:对于数据集A,其data对应的特征为一个向量,此向量所在的空间称为假设空间
1.4 奥卡姆剃刀:若有多个假设与观测一致,则选择最简单的那个
1.5 没有免费的午餐:算法的期望性能与算法本身无关
1.6 偏差方差说明了什么:偏差:学习算法与期望预测的偏离程度,学习算法本身的拟合能力
方差:同样大小训练集的变动导致的学习性能的变化
偏差越小方差越大,方差越小偏差越大
1.7 误差分歧分解说明了什么:个体学习器准确性越高,多样性越大,效果就越好
1.8 机器学习的类型:多分类,二分类,回归,聚类,监督学习,半监督学习,无监督学习
1.9 统计学习:基于统计学泛函分析的机器学习架构
1.10 深度学习:深层神经网络,有多个神经元和多个隐藏层
b
1.11 过拟合:过于学习训练样本中的特点,导致泛化性能下降
1.12 欠拟合:对训练样本中的一般性质尚未学好
1.13 经验误差:在训练集上的误差
1.14 泛化误差:在新样本上的误差
1.15 留出法:将数据集拆分为两个互斥集合,一个作为训练集,一个作为测试集,用于估计训练误差与泛化误差
1.16 自助法:使用放回采样法,采样n次,取原数据集/采样数据集 作为测试集, 采样数据集作为训练集
1.17 交叉验证:将数据集划分成为多个大小相似的互斥子集,尽可能保持子集数据分布的一致性,每次将k-1个子集作为训练集,剩下一个作为测试集,进行k次训练。
1.18 查准率:P = TP / (TP + FP)
1.19 查全率:R = TP / (TP + FN)
1.20 F_1度量:2×P×R / (P+R)
1.21 ROC曲线:通过改变截断点从而得到TPR(y)和FPR(x) TPR = TP / (TP + FN),FPR = FP / (TN + FP)
1.22 AUC面积:ROC曲线所对应的面积
1.23 假设检验:利用假设检验获取两个不同学习器的性能,假设指的是对学习器泛化错误率分布的某种判断或猜想
1.24 信息熵:度量样本集合程度的指标
1.25 gini指数:数据集的纯度可用基尼值去度量,gini系数越小,数据集纯度越高选择划分后,基尼系数最小的那个特征作为划分特征
1.26 Bayes公式: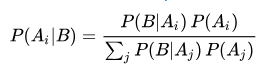
1.27 信息增益:信息增益越大,使用属性a进行的划分纯度越高
1.28 剪枝:决策树算法对于过拟合的解决方法
2
2.1 线性模型
2.1.1 线性模型的优化目标:学习一个线性模型以尽可能准确的预测实值输出标记
2.1.2 线性模型的求解方案:最小二乘法
2.1.3 logistic回归的基本原理: 利用对数激活函数替代单位阶跃函数,解决单位阶跃函数不连续,不处处可导的问题
2.1.4 线性判别分析的基本原理:预使得同类样例的投影点尽可能接近,可以让同类投影点的协方差尽可能小
预使得异类样例投影点尽可能远离,可以让类中心距离尽可能大
2.1.5 ECOC多分类的基本原理:对n个类别进行m次划分,取训练m个分类器,对于一个数据使用这m个分类器,从而得到一个m长的ecoc码,对n个类也能得到n个m长的ecoc码, 找距离最小的码所对应的类别作为数据的类别
2.2 决策树
2.2.1 如何根据信息增益原则划分属性生成决策树:找信息增益最大的属性划分属性生成卷册书
信息增益其实就是信息熵的下降程度
信息增益 = 信息熵 - 划分之后的信息熵按样本量加权平均
2.2.2 剪枝处理的类型和基本方法:预剪枝,后剪枝
预剪枝:在使用信息增益进行划分的时候,判断划分前后验证集精度,以验证集精度是否增加来决定是否划分
后剪枝:后剪枝从后往前遍历每个非叶节点,判断去掉此节点验证集进度是否上升,若上升则去掉此非叶节点
2.2.3 连续值和缺失值的处理:
连续值:将样本中的此属性排序 取t = (ai + ai+1) / 2为阈值,一共有n-1个阈值, 遍历所有的阈值,找到信息增益最大的那个作为截断点,使用截断点将连续值离散的分为两类
缺失值:划分属性时若遇到缺失值那么信息增益为 无缺失值样本所占的比例 × 在无缺失值样本上的信息增益
若数据在此节点有缺失值,那么把此数据按一个概率划入所有的子节点,此概率为p(k,v)
p(k,v)为 未缺失值中此特征为v且为第k类的概率
2.3 神经网络
2.3.1 多层前馈神经网络的基本组成部分:含有输入层,隐藏层,输出层,每层神经元与下一层神经元全连接,不存在同层连接或跨层连接
2.3.2 误差传播算法的原理和步骤:
原理
基于梯度下降策略,以目标负梯度方向对参数进行调整
步骤
1.在(0,1)范围内随机初始化权重和阈值
2.遍历每一个样本,计算器在每个神经元上的权重和阈值的梯度
3.利用梯度和学习率更新权重
4.重复上述操作直到达到停止条件
2.3.3 跳出局部最优的常用策略
1.取多个初值不同的神经网络进行训练,取效果最好的那个
2.使用模拟退火策略
3.使用随机梯度下降
2.4 支持向量机
2.4.1 间隔: 2/ || w||
2.4.2 支持向量:w*x + b
2.4.3 线性可分与不可分:样本可被一个超平面分开和样本不可通过一个超平面分开
2.4.4 核函数:一个非线性映射,将数据从一个线性不可分的空间映射到一个线性可分的空间
2.4.5 软间隔和硬间隔:要求所有样本都划分正确称为硬间隔,允许支持向量机在一些样本上划分错误称为硬间隔
2.4.6 支持向量机分类的优化目标与基本求解方案:
优化目标:0.5*||w||2 + C*Σloss(xi,yi)
基本求解方案:
1.通过拉格朗日乘子法得到对偶问题
2.利用最优化算法求解对偶问题
2.4.7 支持向量回归的基本原理:以f(x)为中心构建了一个宽度为2e的间隔带,若训练样本落入间隔带中则认为被预测准确
2.5贝叶斯分类器
2.5.1 朴素贝叶斯分类器的基本原理:假设数据中的所有特征相互独立,则根据贝叶斯公式有P(c|x) = p(c)Π p(xi |c)
2.5.2 朴素贝叶斯的分类规则 argmaxp(c)Π p(xi |c)
2.5.3 维数过多导致概率趋于0:使用log将连乘变为累加
2.5.3 EM算法的基本原理:
1.根据模型参数和训练样本估计缺省值,使得准确率尽可能高
2.将估计的缺省值作为缺省值,更新模型参数
3.重复上述步骤已达到精度要求
4.原理是最大化模型关于缺省值的边际似然 以估计缺省值
2.6 集成学习
2.6.1 基本原则:好而不同
好:个体学习器准确率尽可能高
不同:各学习器关联性低
2.6.2 集成学习类型:
1.boosting
先训练出一个学习器,然后基于前学习器的错误训练样本对训练样本的分布进行调整,使得后续学习器更加关注之前学习器预测错误的训练样本
最终为所有学习器的加权结合
2.bagging
基于自助采样法,采样出T个含有m个训练样本的采样集,然后基于每个采样集训练出一个基学习器,再将这些学习器进行结 ?/
其对分类任务使用简单投票法,对回归任务使用简单平均法
3.随机森林
在以决策树为基学习器构建Bagging集成的基础上,进一步在决策树的训练过程中引入随机属性选择,在RF中,对及决策树的每一个结点,先从该结点的属性集合中随机选择一个包含k个属性的子集,然后从这个子集中学则一个最优的属性用于划分,推荐k=log2d
2.7 聚类:
2.7.1.学习方法分类
监督学习:当有大量标记过的样本数据时采用
半监督学习:当有少量标记过的样本数据和大量未标记的样本数据时采用
主要思路:
1.利用已标记的样本,得到模型
2.利用模型估计未标记的样本
3.利用预测值重新训练模型
4.重复2,3步直到模型达到要求
无监督学习:当样本数据没有标记时采
2.7.2:K-means的基本原理
1.随机选取k个聚类中心
2.每个数据找离自己距离最短的聚类中心,进行分类
3.计算每个类别的中心点,将他们作为真正的中心点
4.重复2,3步直到均方误差收敛
5.重复1-4步多次,选取均方误差最小的作为结果



