信息论-复习笔记

典型序列:

　　信源有p个编码，，，，每个编码有一个出现的概率

　　那么对于这个信源发出的n长序列

　　一共有pⁿ个n长序列

　　其中有一小部分，出现的概率较大，称为典型序列

　　其他的序列，出现的概率特别小，称为非典型序列

计算典型序列的概率:

　　 2^{-N(H(x) + ε)}　<= p <=　2^{-N(H(x) - ε)}

　　 ε表示，将序列出现的概率>ε作为典型序列

　　 N:序列长度

　　当N->∞时 典型序列出现的次数T_x(N,ε) = 2^NH(x)

 

最优二元即时码

　　二元霍夫曼编码

 

霍夫曼编码:

　　n元霍夫曼编码，一共有m个字符

　　将信源出现的概率排序

　　第一次取m % (n-1)个最小的进行合并

　　之后每次合并n个

　　当只剩下一个的时候再进行展开

　　这样就得到了霍夫曼编码

　　展开时，从大到小使用0,1,2，，，，n-1

　　解题格式如下

　　

 

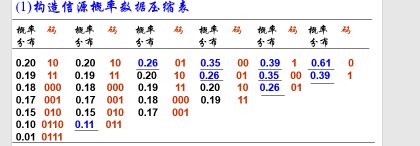
 马尔科夫信源

　　马尔科夫信源有几种状态S_i

　　状态之间有概率去相互转化

　　那么通过求解线性方程组可以求出每个状态出现的概率P(S_i)

　　通过P(S_i)也可以求出每个字母出现的概率

　　H(x|S_i)是在S_i下，信源的熵

　　H_∞(x) = ΣP(S_i) * H(x|S_i)  叫做熵率

　　p1                p1

　　p2  =  P.T * p2

　　P为概率转移矩阵

　　平均码长:

　　　　对字母按概率进行2元霍夫曼编码

　　　　也可计算编码的码长

 

　　η = H(x) / (l * log r)  编码效率  l:平均码长 r字母的个数

 

信道的最佳译码规则，最大似然译码规则，平均差错率

　　概率转移矩阵Q

　　

　　　q(b|a)表示当信道输入为a时，输出为b的概率

 

　　  最大似然译码准则

　　  将每一列的最大值找出

　　   对应的q(b_i|a_j)作为F(b_i) = a_j

 

　　　最佳译码准则

　　　将Q的每一个数q(b_i|a_j)乘对应的p(a_j)得到矩阵P

　　　还是取找p每一列的最大值,并将其作为F(b_i) = a_j

　　　　

　　   平均差错率根据编码和矩阵P使用1-Σp_正确即可算出平均差错率