最优化-罚函数法,乘子法
罚函数法:
求解约束条件下的最优化问题
罚函数法的思路就是改变函数f(x),将f(x) 变为F(x)
使得F(x)在无约束条件下取得的最优解,正好符合我们的约束条件,且正好为f(x)在约束条件下的最优解
先有最优化问题f(x), 可行区域是c(x) <= 0
外罚函数法:
对于F(x)在可行区域内仍是f(x),在可行区域外,对函数加上惩罚即可
F(x) = f(x) c(x) <=0
F(x) = f(x) + α/2 (c(x))2
可以改写为F(x) = f(x) + α/2 (max(c(x), 0)2)
对于一般的约束条件c1(x) <=0 ,,,,,,,cn(x) <= 0
F(x) = f(x) + α/2 (max(c1(x)2, ,,,,,,,cn(x)2,,0)
记(max(c1(x)2, ,,,,,,,cn(x)2,,0)为S(x)
可以看到,当α -> +∞时,F(x)在无约束条件下的最优解符合条件
算法流程:
选择递增序列 αk 此序列趋近于 +∞
选定初始点x0
对于第i次迭代,求解无约束最优化问题F(x) = f(x) + αi/2 (max(c1(x)2, ,,,,,,,cn(x)2,,0)标志
终止条件: αi * S(xi) < e
此时将xi记为最优化问题的解
一般可用 αi = 2i作为序列
缺点:
当迭代次数较多时,αi会特别大,导致Hesse矩阵的条件数特别大,这就给求解无约束最优化问题带来了困难
求出来的解可能在约束区域之外
内罚函数法
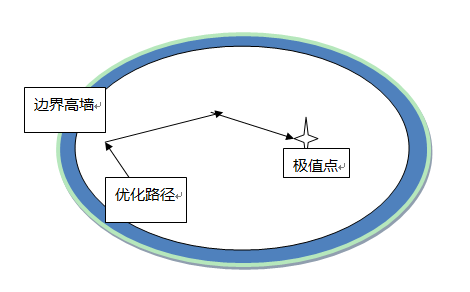
相比于外罚函数法在不可行区域加惩罚,内罚函数法在可行域边界筑起高墙,让目标函数无法穿过,就把目标函数挡在可行域内了。
这种惩罚策略只适用于不等式约束问题,并要求可行域的内点集非空,否则,每个可行点都是边界点,都加上无穷大惩罚,惩罚也就失去意义了。
考虑不等式约束:
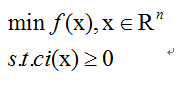
当x从可行域
的内部趋近于边界时,则至少有一个ci(x)趋近于零,因此,不难想到可构造如下的增广的目标函数:
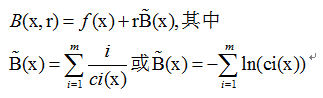
称为内罚函数或障碍函数,参数r仍称为罚因子。
上述的内罚函数,当x靠近边界时,会迅速增大,迫使在可行域之内进行求解。
如下图:
具体算法:
同外罚函数法类似,我们考虑用迭代算法来求解。每次变化得到一个罚因子rk,从前一步关于罚因子rk-1的最优解出发,得到下一步关于rk的最优解;当满足条件是,迭代结束,得到近似最优解。
经证明,内罚函数法也是收敛的,迭代结束的条件为
步骤如下:
优点: 解决了外罚函数解可能在可行域外的问题
缺点:也可会出现求解无约束优化问题困难的情况
乘子法
乘子法是将函数约束加上了乘子而已


考试时,若要用到乘子法或者罚函数法,一般是利用alaph -> 无穷来求出正确解


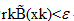


 浙公网安备 33010602011771号
浙公网安备 33010602011771号