多元统计分析-协方差,相关系数
协方差
协方差用来描述两个变量的相关性
若两个随机变量正相关则cov(x,y) > 0
负相关则cov(x,y)<0
不相关则cov(x,y) = 0
公式 cov(x,y) = E[(x-ux) *(y-uy)]
rxy = cov(x,y) / ( sqrt(cov(x,x)) * sqrt(cov(y,y)) )
就是求x - x的均值 与 y-y的均值的乘积的期望
因为若两个向量正相关则对于多数的(x,y), (x-ux) *(y-uy) > 0, 其期望自然也就大于0
若两个向量负相关则对于多数的(x,y), (x-ux) *(y-uy) < 0, 其期望自然也就小于0
若两个向量完全不相关则(x-ux) *(y-uy) 有时大于0,有时小于0,其期望等于0
相关系数:
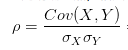 σ:方差
σ:方差
相关系数是消除了量刚(尺度)的协方差
比如X是均值为1000的随机变量 Y是均值为0的随机变量, 先将其标准化处理再计算协方差就是相关系数
-1<=p<=1
相关系数为1表示完全正相关,为-1表示负相关,为0表示完全不相关
术语解释:
标准化:
对于均值为u, 方程为a的正太分布随机变量X
可通过Y =(x-u)/a将其变为均值为0方差为1的正太分布随机变量Y



 浙公网安备 33010602011771号
浙公网安备 33010602011771号