信息论-熵

定义

　　熵是从整个集合的统计特性所考虑的

　　表示信源输出前信源的平均不确定性

　　表示信源输出后每个符号携带的平均信息

 

　　I(p)只能表示信源中每个符号的信息量，不能作为信源总体的信息量

公式:

　　H(x) = E(log 1/p(a_i))

   　　　 = -∑p(a_i) log p(a_i)

 

自信息

　　发出的消息所携带的信息量， 用I(x)计算

　　在消息a中每个符号携带的平均信息量 自信息/符号个数

　　自信息不是熵　　

 

联合熵与条件熵

　　对于信源来说∑p(a_i) = 1

　　对于联合熵来说∑∑p(a_ia_j) = 1

　　p(a_ia_j) = p(a_i|a_j) * p(a_j)

　　 若信源的输出与上一个输出的字符有关系 上一个字符为a_j的话，这一个为a_i个概率为 p(a_i|a_j)

　　联合熵为H(x_ix_j)  = -∑∑p(a_ia_j) log p(a_ia_j) 用于表示信源输出长度为2的平均不确定性

　　条件熵为H(x_i|x_j)  = -∑∑p(a_i|a_j) p(a_j)log p(a_i|a_j)=-∑∑p(a_ia_j) log p(a_i|a_j) 随机序列x_ix_j的联合符号集上的条件自信息量的数学期望

 

　　用公式可以推出

       

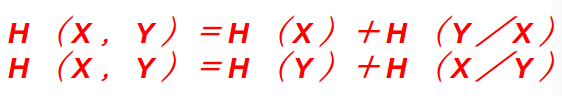
熵的意义

　　H(X)：表示信源中每个符号的平均信息量（信源熵）

　　H(Y)：表示信宿中每个符号的平均信息量（信宿熵）

　　H(X|Y)：表示在输出端接收到Y的全部符号后，发送端X尚存的平均不确定性。这个对X尚存的不确定性是由于干扰引起的。信道疑义度(损失熵，含糊度)

　　H(Y|X)：表示在已知X的全部符号后，对于输出Y尚存的平均不确定性。信道散布度(噪声熵)

　　H(XY)：表示整个信息传输系统的平均不确定性（联合熵）

 

 一些性质

　　1.对称性:   H(P) 的取值与分量 p1, p2 , ··· , pq的顺序无关

　　2.确定性：信源是确知信源时，其熵为0

　　3.非负性：H(p) >= 0

　　4.扩展性：　　

　　5.可加性：当X,Y为独立信源时 H(X,Y) = H(X)+ H(Y) 

　　6.强可加性：对于任意信源都有H（X,Y）=H（X）+ H（Y|X）

　　7.递增性：若原信源 X 中有一个符号分割成了m个元素(符号)，这m个元素的概率之和等于原元素的概率，而其他符号的概率不变，则新信源的熵增加等于由分割而产生的不确定性量

　　　　　　　　

　　8.上凸性：熵函数H(P)是概率矢量P＝(p1，p2， …，pq)的严格∩型凸函数(或称上凸函数)

　　9.极值性：

　　

　　10. H(X,Y) >= H(X)　　

　　最大离散熵定理：在离散信源情况下，信源各符号等概率分布时，熵值达到最大