Pytorch1.0深度学习:损失函数、优化器、常见激活函数、批归一化详解
不用相当的独立功夫,不论在哪个严重的问题上都不能找出真理;谁怕用功夫,谁就无法找到真理。
本文主要介绍损失函数、优化器、反向传播、链式求导法则、激活函数、批归一化。
1 经典损失函数
1.1交叉熵损失函数——分类
(1)熵(Entropy)
变量的不确定性越大,熵也就越大,把它搞清楚所需要的信息量也就越大。log以2为底!
H(x) = E[I(xi)] = E[ log(2,1/p(xi)) ] = -∑p(xi)log(2,p(xi)) (i=1,2,..n)
(2)交叉熵(Cross Entropy)
主要用于度量两个概率分布间的差异性信息。差异性越小,交叉熵值越小!
H(p, q) = ∑p(xi)log(2,q(xi))
H(p, q) = H(p) + DkL(p/q)
DkL(散度,KL-Divergence)越小越好
DkL(p/q) = ∑P (xi)log(P(xi)/Q(xi) )
DkL(p/q) = ∑P (xi)log(P(xi)) - ∑P (xi)log(Q(xi))
则,H(p, q) = - ∑P (xi)log(Q(xi)
对于one-hot 编码
Entrop = 1log1 = 0
二分类举例Binary Classification:
H(P,Q) = -P(cat)logQ(cat)-(1-p(cat))log(1-Q(cat))
P(dog) = (1-P(cat))
H(P,Q) = -∑p(xi)log(Q(xi)) ; i=(cat,log)
=-P(cat)logQ(cat)- p(dog)log(1-Q(cat))
= -(ylog(p)+(1-y)log(1-p))
多分类举例:
P1 = [1 0 0 0 0] —> label
Q1 = [0.4 0.3 0.05 0.05 0.2] —>pred
H(P1,Q1) = -∑p(xi)log(Q(xi)) ; i=range(5)
= -(1*log(0.4) + 0*log(0.3) + 0*log(0.05)+0*log(0.05)+0*log(0.2))
= -log(0.4)
≈ 0.916
Q1 = [0.98 0.01 0 0 0.01] —>pred
H(P1,Q1) = --∑p(xi)log(Q(xi)) ; i=range(5)
= -(1*log(0.98) + 0*log(0.01) + 0*log(0)+0*log(0)+0*log(0.01))
= -log(0.98)
≈ 0.02
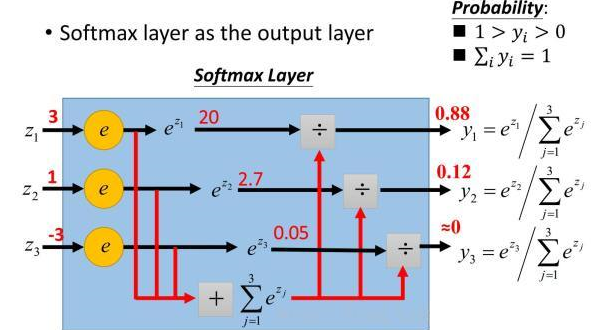
(3)Softmax函数
假设原始的神经网络输出为y1, y2, y3, ..., yn,那么经过softmax回归处理之后的输出为:
softmax(y)i = y'i = eyi / (Σnj=1eyj)
这个新的输出,可以理解为经过神经网络的推导,一个样例为不同类别的概率分别是多少大。

1 #调用softmax函数 2 import torch 3 import torch.nn.functional as F1 4 a = torch.randint(3,10,(2,3),dtype=torch.float)#.long() 5 print(a) 6 b = F1.softmax(a,dim = 1) 7 b 8 9 输出: 10 tensor([[3., 7., 4.], 11 [3., 5., 8.]]) 12 tensor([[0.0171, 0.9362, 0.0466], 13 [0.0064, 0.0471, 0.9465]]) 14 15 #自定义softmax 16 for i in a: 17 sum_exp = torch.tensor([0],dtype=torch.float) 18 for k in i: 19 simpleexp = torch.exp(k) 20 sum_exp+=simpleexp 21 print(simpleexp,sum_exp) 22 print("**************************",i) 23 for j in i: 24 simpleexp = torch.exp(j) 25 print(simpleexp,simpleexp/sum_exp) 26 print("***********结束一轮***************") 27 28 输出: 29 tensor(20.0855) tensor([20.0855]) 30 tensor(1096.6332) tensor([1116.7188]) 31 tensor(54.5981) tensor([1171.3169]) 32 ************************** tensor([3., 7., 4.]) 33 tensor(20.0855) tensor([0.0171]) 34 tensor(1096.6332) tensor([0.9362]) 35 tensor(54.5981) tensor([0.0466]) 36 ***********结束一轮*************** 37 tensor(20.0855) tensor([20.0855]) 38 tensor(148.4132) tensor([168.4987]) 39 tensor(2980.9580) tensor([3149.4568]) 40 ************************** tensor([3., 5., 8.]) 41 tensor(20.0855) tensor([0.0064]) 42 tensor(148.4132) tensor([0.0471]) 43 tensor(2980.9580) tensor([0.9465]) 44 ***********结束一轮***************
(4)pytorch中softmax交叉熵损失函数,利用的是cross_entropy()函数
在Pytorch里,nn.Cross_Entropy()损失函数已经将softmax()函数——>log2()函数——>nll_loss()函数绑在一起。因此,使用了Cross_Entropy()函数,函数里的paramets必须是logits。全连接层后面不需要再添加softmax层,此处也是与TensorFlow不同之处。
例如:
x = torch.randn(1,784)
w = torch.randn(10,784)
logits = x@w.t()
第一种,自写交叉熵函数
pred = F.softmax(logits,dim = 1)
pred_log = torch.log(pred)
F.nll_loss(pred_log,torch.tensor([3]))
第二种,直接调用cross_entropy()函数
F.cross_entropy(logits, torch.tensor([3]))
input = torch.randn(3, 5) # each element in target has to have 0 <= value < C target = torch.tensor([1, 0, 4]) input_temp = F.log_softmax(input,dim=1) print(input0) output = F.nll_loss(input_temp, target) output 输出: tensor([[-3.1498, -1.7311, -0.9935, -2.9399, -1.0303], [-2.4030, -1.2345, -1.9903, -1.0578, -2.0046], [-0.6991, -1.8396, -2.3656, -2.2445, -1.9366]]) tensor(2.0236)
1.2 均方误差nn.MSELoss()——回归
与分类问题不同,回归问题解决的是对具体的数值进行预测。例如,房价预测、销量预测都是回归问题。这些问题需要预测的不是一个事先定义好的类别,而是一个任意实数,解决回归问题的神经网络一般只有一个输出节点,这个节点的输出值就是预测值。对于回归问题常用的损失函数为均方误差(MSE,mean squared error)。
![]()
注:yi为一个batch中第i个数据的正确答案,而为神经网络计算出的预测值。
2 反向传播
反向传播算法就是一个有效的求解梯度的算法,本质上其实就是一个链式求导法则的应用。
2.1链式法则
链式法则是微积分中的求导法则,用于求一个复合函数的导数,是在微积分的求导运算中一种常用的方法。
例如:
f(x,y,z) = (x+y)z
本来可以直接求出函数的关于x、y、z的导数,但是此次采用链式求导法则
令 q = x+y
则 f = qz
对于这两个式子分别求出它们的微分∂f / ∂q = z, ∂f / ∂z = q,其中,∂q / ∂y = 1, ∂q / ∂x = 1
因需要求出∂f / ∂y,∂f / ∂x,∂f / ∂z,那么f(x,y,z)的连续求导为:
∂f / ∂x = (∂f / ∂q) * ( ∂q / ∂x) = z
∂f / ∂y = (∂f / ∂q) * ( ∂q / ∂y) = z
∂f / ∂z = q = x + y
以上便是链式求导法则的核心,通过连续求导,便得出了∂f / ∂y,∂f / ∂x,∂f / ∂z。
2.2神经网络优化算法——梯度下降算法 torch.optim
参数的梯度可以通过求偏导的方式计算,对于参数Θ,其梯度为∂J(Θ)/∂Θ, 有了梯度,还需要定义一个学习率来定义每次参数更新的幅度,则得到参数更新的公式为:
Θi = Θi-1 - η▽J(Θi-1)
2.2.1 SGD
随机梯度下降法(Stochastic Gradient Descent):每次使用一批(batch)数据进行梯度的计算。而不是计算全部数据的梯度,因为现在的深度学习的数据量都特别大,所以每次都计算所有数据的梯度是不现实的,这样会导致运算的时间特别的长,并且每次都计算全部的梯度还失去了一些随机性,容易陷入局部误差,所以,SGD能减小收敛所需要的迭代次数,使用随机梯度下降法可能每次都不是朝着真正最小的方向,但是这样反而容易跳出局部极小点。
w:要训练的参数
J(w):代价函数
▽wJ(w):代价函数的梯度
η:学习率
w = w-η*▽wJ(w; x(i); y(i))
2.2.2 Momentum
Momentum就是在随机梯度下降的同时,增加动量,可以把它理解为增加惯性,可解释为利用惯性跳出局部极小值点。
γ:动量因子,通常设置为0.9
vt = γvt-1 + η*▽wJ(w)
w = w - vt
2.2.3 Adagrad
Adagrad优化器,原始论文(http://www.jmlr.org/papers/volume12/duchi11a/duchi11a.pdf)。
i:代表第i个分类
t:代表出现次数
ε:避免分母为0,取值一般为1e-8
η:取值一般为0.01
γ:动量因子,通常设置为0.9
gt,i = ▽wJ(wi)
wt+1 = wt-[η/(Σtt'(gt',i)2+γ)1/2+ε]*gt
它是基于SGD的一种算法,它的核心思想是对比较常见的数据给与它比较小的学习率去调整参数,对于比较罕见的数据给予它比较大的学习率去调整参数,适合用于数据稀疏的数据集。Adagrad主要的优势在于不需要人为的调节学习率,它可以自动调节。它的缺点在于,随着迭代次数的增多,学习率也会越来越低,最终会趋向于0.
2.2.4 RMSprop
RMSprop不会再将前面有所的梯度求和,而是通过一个衰减率将其变小,使用了一种平滑平均的方式,越靠前面的梯度对自适应的学习率影响越小,这样就能更加有效地避免Adagrad学习率一直递减太多的问题,能够更快的收敛。[http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf]
RMS(Root Mean Square)是均方根的缩写
γ:动力,通常设置为0.9
ε:避免分母为0,取值一般为1e-8
η:取值一般为0.01
E[g2]t:表示前t次的梯度平方的平均值
gt = ▽wJ(w)
E[g2]t =γ E[g2]t-1 - (1-γ)g2t
wt+1 = wt-[η/(E[g2]t+ε)1/2]*gt
· RMSprop借鉴了一些Adagrad的思想,不过PMSprop只用到了前t-1次梯度平方的平均值加上当前梯度的平方的和的开方作为学习率的分母。这样RMSprop不会出现学习率越来越低的问题,而且也能自己调节学习率,并且可以有一个比较好的效果。
2.2.5 Adam
Adam是一阶基于梯度下降的算法,基于自适应低阶矩估计优化器。效果比RMSprop好,Adam论文https://arxiv.org/abs/1412.6980 。其还有一种Adamax优化算法是基于无穷大范数的Adam算法的一个变种。
β1:一阶矩估计的指数衰减率,一般取值0.9
β2:二阶矩估计的指数衰减率,一般取值0.999
gt = ▽wJ(w)
mt = β1mt-1+(1-β1)gt
vt = β2vt-1+(1-β2)g2t
m't = mt / (1-βt1)
v't = vt / (1-βt2)
wt+1 = wt - η / [ (v't)1/2 + ε ]*m't
Adam像Adadelta和RMSprop一样会存储之前衰减的平方梯度,同时它也会保存之前衰减的梯度。经过一些处理之后再使用类似Adadelta和RMSprop的方式更新参数。
3常见激活函数
作用:把卷积层输出结果做非线性映射。例如:sigmoid tanh Relu Leaky Relu ELU Maxout。
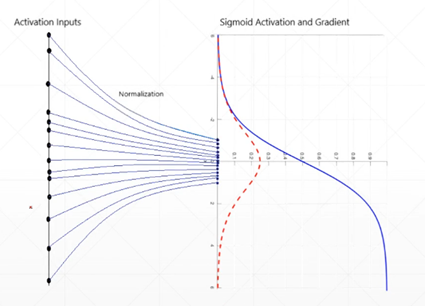
3.1 Sigmoid
Sigmoid函数曾被广泛地应用,但由于其自身的一些缺陷,现在很少被使用了。torch.nn.functional.sigmoid(input)
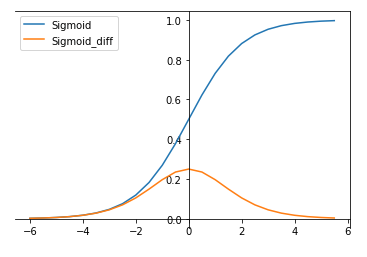
Sigmoid函数被定义为:σ(x) = 1/(1+exp(-x))
其导数为:dσ(x)/dx = σ(x)(1-σ(x))
优点:
(1)sigmoid函数的输出映射在(0,1)之间,单调连续,输出范围有限,优化稳定,可以作用输出层。
(2)求导容易。
缺点:
(1)容易出现梯度消失(gradient vanishing)现象,当激活函数接近饱和区时,变化缓慢,导数接近0,当进行反向传播时,当前导数需要之前各层导数的乘积,较小的数相乘,导数结果很接近0。
(2)Sigmoid的输出均值不是0(zero-centered)
(3)指数运算相对耗时
3.2 tanh
tanh函数是双曲函数中的一个,为反曲正切。torch.nn.functional.tanh(input)
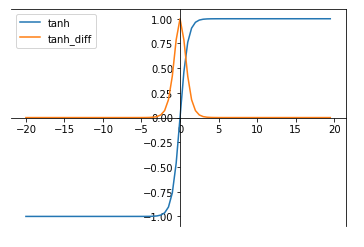
tanh函数被定义为:tanh(x) = (exp(x)-exp(-x))/(exp(x)+exp(-x))
其导函数为:d(tanh(x))/dx = 4 / (exp(x)+exp(-x))2
优点:
(1)比sigmoid函数收敛速度更快。
缺点:
(1)依然没有改变sigmoid函数的最大问题,其饱和性产生的梯度消失。
3.3 ReLU
ReLU函数用来替代传统的激活函数。
torch.nn.functional.relu(input, inplace = False)
ReLU函数被定义为:Relu(x) = max(0,x)
其导函数为:f(x) = 0 if x<0 else f(x) = 1

优点:
(1)比sigmoid和tanh函数收敛速度快,求导方便
(2)不存在梯度消失问题
(3)计算复杂度低,不进行指数运算
缺点:
(1)ReLU输出的均值为非0
(2)存在神经元坏死现象(Dead ReLU Problem),某些神经元可能永远不会被激活,导致相应参数永远不会被更新(在负数部分,梯度为0)
(3)不会对数据做规范化(压缩)处理,使得数据的幅度随模型层数的增加而不断增大。
3.4 Leakly ReLU
Leakly ReLU函数用来替代传统的激活函数。其函数定义为:f(x) = max(0.01x,x)
导函数为:f(x) = 0.01 if x<0 else f(x) = 1
torch.nn.functional.leaky_relu(input, negative_slope=0.01, inplace=False)

此激活函数的提出是用来解决ReLU带来的神经元坏死的问题,可以将0.01设置成一个变量a,可以由反向传播学习。但其表现并不一定比ReLU好。
3.5 EReLU
拥有Relu的所有优点,不会出现梯度消失的情况,输出均值趋于0,但是因为指数存在,计算量略大。
f(x) = x if x>0 else f(x) = α(exp(x)-1)
3.6 Maxout
max(wT1*x+b1, wT2*x+b2)
计算是线性的,梯度不会饱和不会消失。
参数较多。
4 Dropout函数
Dropout函数是Hintion在2012年提出的,为了防止模型过拟合,在每个训练批次中,通过忽略一般的神经元即让一部分的隐层节点值为0,可明显地减少过拟合现象。
torch.nn.functional.dropout(input, p = 0.5,training = False,inplace = False)
torch.nn.functional.alpha_dropout(input, p = 0.5,training = False)
torch.nn.functional.dropout2d(input, p = 0.5,training = False,inplace = False)
torch.nn.functional.dropout3d(input, p = 0.5,training = False,inplace = False)
注:pytorch中的p = 0.5,表示的是dropout_prob;而TensorFlow中的p = 0.5,表示keep_prob。
5 Image Normalization、BN
5.1 Image Normalization
Image Normalization是在数据增强的过程中使用,同样是使得三个通道的数据保持均值为0,方差为1的分布中。
transforms.Normalize(mean = [0.485, 0.456, 0.406], std = [0.229, 0.224, 0.225])
5.2 Batch Normalization
批归一化(Batch Normalization),顾名思义就是对每个批次的数据分别求出其均值与方差,然后根据均值和方差对每个批批次的数据进行标准化(即将一批不服从标准分布的数据,变得符合标准分布)。其算法流程图,如下所示,其中伽马和贝塔是需要学习的参数。

Batch Normalization的好处是什么?
1、 在测试数据上的准确率更高;(图a,b展示的是网络的最后一个隐藏层,每个batch数据的分布)在原始网络中的分布随时间发生显著变化,包括平均值和方差,但是在批标准化的网络中分布却更加稳定,有助于训练。很少的迭代次数,便得到较高的准确率,减少了训练网络的时间。
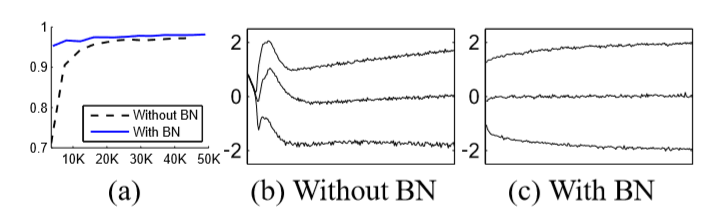
2、 相对于传统的网络结构,太高的学习率可能会导致梯度消失或爆炸,或者陷入局部极小值点,但是添加了Batch Normalization,可很好的处理了这个问题。因此便可以加大学习率,减少网络训练的时间。
3、 实验表明,将dropout层用batch normalization层代替,并没有出现过拟合。
4、 并且减少了L2的权重系数。
注:在pytorch中的layer.running_mean和layer.running_var统计的是全局的均值与方差,并不是单层的均值与方差。





