树与树算法
一、树的基本概念
(一)什么是树
数是一种抽象数据类型(ADT),用来模拟具有树状结构性质的集合,它是由n(n>=1)个有限节点组成一个具有层次关系的集合。树具有以下性质:
- 每个节点有零个或多个子节点;
- 没有父节点的节点称为根节点;
- 每一个非根节点有且只有一个父节点;
- 除了根节点外,每个子节点可以分为多个不相交的子树;

树中涉及的术语有:
- 节点的度:一个节点含有的子树的个数称为该节点的度(B节点的度为3);
- 树的度:一棵树中,最大的节点的度称为树的度(上述树的度是B节点的度);
- 叶节点或终端节点:度为零的节点(O、P、Q节点);
- 父亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点(B节点是D、E、F节点的父节点);
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点(D、E、F节点是B节点的孩子节点);
- 兄弟节点:具有相同父节点的节点互称为兄弟节点(B、C是兄弟节点);
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次(上述树的高度为5);
- 堂兄弟节点:父节点在同一层的节点互为堂兄弟(D、G节点是堂兄弟节点);
- 节点的祖先:从根到该节点所经分支上的所有节点(Q节点的祖先是A、C、H、N节点);
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙(B节点的子孙是D、E、F、I、J、O节点)。
- 森林:由m(m>=0)棵互不相交的树的集合称为森林;
(二)数的种类
树分为无序树和有序树,所谓无序树就是树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树;这种树也就没什么研究价值。有序树就是树中任意节点的子节点之间有顺序关系,其包含:
- 二叉树
- 霍夫曼树
- B树
下面就着重说明二叉树的相关概念以及实现过程。
二、二叉树
(一)什么是二叉树
二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树具有的性质:
- 在二叉树的第i层上至多有2^(i-1)个结点(i>0)
- 深度为k的二叉树至多有2^k - 1个结点(k>0)
- 对于任意一棵二叉树,如果其叶结点数为N0,而度数为2的结点总数为N2,则N0=N2+1;
- 具有n个结点的完全二叉树的深度必为 log2(n+1)
- 对完全二叉树,若从上至下、从左至右编号,则编号为i 的结点,其左孩子编号必为2i,其右孩子编号必为2i+1;其双亲的编号必为i/2(i=1 时为根,除外)
二叉树分为完全二叉树和满二叉树。
- 完全二叉树
若设二叉树的高度为n,除第n层外,其它各层 (1~n-1) 的结点数都达到最大个数,第n层有叶子结点,并且叶子结点都是从左到右依次排布,这就是完全二叉树。

1-n-1层与满二叉树一样,第n层没有挂满,只有前边挂满了节点。
- 满二叉树
除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

(二)二叉树的实现
二叉树实现下面的方法:
- add 构建二叉树
- breadth_travel 二叉树的广度遍历
- pre_order 二叉树深度遍历中的前序遍历
- middle_order 二叉树深度遍历中的中序遍历
- after_order 二叉树深度遍历中的后序遍历
树中的深度优先遍历一般用递归,广度优先遍历一般用队列,广度优先遍历从上到下从从左到右遍历整个树的节点;深度优先遍历有三种方式,分别是前序遍历、中序遍历以及后序遍历:
- 前序遍历
访问顺序是:根-->左子树-->右子树
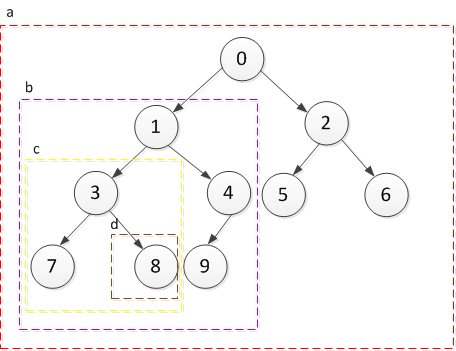
上图中二叉树的先序遍历:
(1)a是二叉树,首先遍历0
(2)b是左子树,然后根据先序遍历 根-->左子树-->右子树,所以遍历的是左子树的根也就是1
(3)c是b的左子树,所以同上面一样遍历3、7、8
(4)b的右子树,4、9
(5)a的右子树,2、5、6
最终的顺序就是0、1、3、7、8、4、9、2、5、6
- 中序遍历
访问顺序是:左子树-->根-->右子树,还是根据上面的图:
(1)a的左子树是b,b的左子树是c,c的左子点是7
(2)c的根节点和右节点分别是3、8
(3)b树的根是1
(4)b树的右子树排序9、4
(5)a树的根以及右子树进行排序0、5、2、6
最终的顺序就是7、3、8、1、9、4、0、5、2、6
- 后序遍历
访问顺序是:左子树-->右子树-->根,还是根据上面的图,最终的顺序就是7、8、3、9、4、1、5、6、2、0
代码实现:
class Node: def __init__(self, item): self.elem = item self.lchild = None self.rchild = None class Tree: """二叉树""" def __init__(self): self.root = None def add(self, item): node = Node(item) if not self.root: self.root = node return queue = [self.root] while queue: cur_node = queue.pop(0) if not cur_node.lchild: cur_node.lchild = node return else: queue.append(cur_node.lchild) if not cur_node.rchild: cur_node.rchild = node return else: queue.append(cur_node.rchild) def breadth_travel(self): """广度遍历""" if not self.root: return queue = [self.root] while queue: cur_node = queue.pop(0) print(cur_node.elem, end=" ") if cur_node.lchild: queue.append(cur_node.lchild) if cur_node.rchild: queue.append(cur_node.rchild) def pre_order(self, node): """先序遍历""" if not node: return print(node.elem, end=" ") self.pre_order(node.lchild) self.pre_order(node.rchild) def middle_order(self, node): if not node: return self.middle_order(node.lchild) print(node.elem, end=" ") self.middle_order(node.rchild) def after_order(self, node): if not node: return self.after_order(node.lchild) self.after_order(node.rchild) print(node.elem, end=" ") if __name__ == '__main__': tree = Tree() tree.add(0) tree.add(1) tree.add(2) tree.add(3) tree.add(4) tree.add(5) tree.add(6) tree.add(7) tree.add(8) tree.add(9) tree.breadth_travel() # 0 1 2 3 4 5 6 7 8 9 print('\n') tree.pre_order(tree.root) # 0 1 3 7 8 4 9 2 5 6 print('\n') tree.middle_order(tree.root) # 7 3 8 1 9 4 0 5 2 6 print('\n') tree.after_order(tree.root) # 7 8 3 9 4 1 5 6 2 0
在深度优先遍历中如果给出前序、中序或者后序、中序均可以推断树的结构,但是只有前序、后序是无法推断树的结构。比如:
0 1 3 7 8 4 9 2 5 6 7 3 8 1 9 4 0 5 2 6
分别是前序、中序,可以推断树的结构:
(1)根据前序是 根-->左子树-->右子树
(2)所以前序中的0是根,将下面的中序分成两部分,0的左边又通过前序的1进行分
(3)重复(1)(2)步骤即可



