概率与数理统计-蒙特卡洛之拒绝采样

声明

转：> https://blog.csdn.net/u010159842/article/details/78959515

介绍

蒙特卡洛（Monte Carlo）方法是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明，而被提出的一种以概率统计理论为基础的数值计算方法。它的核心思想就是使用随机数（或更常见的伪随机数）来解决一些复杂的计算问题。

当所求解问题可以转化为某种随机分布的特征数（比如随机事件出现的概率，或者随机变量的期望值等）时，往往就可以考虑使用蒙特卡洛方法。通过随机抽样的方法，以随机事件出现的频率估计其概率，或者以抽样的数字特征估算随机变量的数字特征，并将其作为问题的解。这种方法多用于求解复杂的高维积分问题。

实际应用中，我们所要面对的第一个问题就是如何抽样？在统计学中， 抽样（或称采样）是指从目标总体中抽取一部分个体作为样本的过程。

例如，我们想知道一所大学里所有男生的平均身高。但是因为学校里的男生可能有上万人之多，所以为每个人都测量一下身高可能存在困难，于是我们从每个学院随机挑选出100名男生来作为样本，这个过程就是抽样

但是在计算机模拟时，我们所说的抽样，其实是指从一个概率分布中生成观察值（observations）的方法。而这个分布通常是由其概率密度函数（PDF）来表示的。而且，即使在已知PDF的情况下，让计算机自动生成观测值也不是一件容易的事情。从本质上来说，计算机只能实现对均匀分布（Uniform distribution）的采样。

具体来说，我们可能要面对的问题包括：

• 计算机只能实现对均匀分布的采样，但我们仍然可以在此基础上对更为复杂的分布进行采样，那具体该如何操作呢？
• 随机分布的某些数字特征可能需要通过积分的形式来求解，但是某些积分可能没有（或者很难求得）解析解，彼时我们该如何处理呢？
• 在贝叶斯推断中，后验概率的分布是正⽐于先验和似然函数之积的，但是先验和似然函数的乘积形式可能相对复杂，我们又该如何对这种形式复杂的分布进行采样呢？

Inverse CDF 方法

比较简单的一种情况是，我们可以通过PDF与CDF之间的关系，求出相应的CDF。或者我们根本就不知道PDF，但是知道CDF。此时就可以使用Inverse CDF的方法来进行采样。这种方法又称为逆变换采样（Inverse transform sampling）。

如果你对PDF和CDF的概念有点模糊，我们不妨先来一起回顾一下它们的定义。对于随机变量\(X\)，如下定义的函数 \(F\):

\[F(x)=P\{X<= x\}, -\infty < x < \infty \]

称为 \(X\) 的累积分布函数（CDF，Cumulative Distribution Function）。对于连续型随机变量 \(X\) 的累积分布函数 \(F(x)\)，如果存在一个定义在实数轴上的非负函数 \(f(x)\)，使得对于任意实数 \(x\)，有下式成立：

\[F(x)=\int_{-\infty}^{\infty}{f(t)}dt \]

则称 \(f(x)\) 为 \(X\) 的概率密度函数（PDF，Probability Density Function）。显然，当概率密度函数存在的时候，累积分布函数是概率密度函数的积分。

所以，通常我们可以通过对PDF（如下图中的左图所示为正态分布的PDF）进行积分来得到概率分布的CDF（如下图中的右图所示为正态分布的CDF）。然后我们再得到CDF的反函数 \(F^{-1}(u)\)，如果你想得到 \(m\) 个观察值，则重复下面的步骤 \(m\) 次:

• 从 Uniform(0,1) 中随机生成一个值（前面已经说过，计算机可以实现从均匀分布中采样），用 \(u\) 表示。
• 计算 \(F_{-1}(u)\) 的值 \(x\)，则 \(x\) 就是从 \(f(x)\) 中得出的一个采样点。

以下图为例，如果从 Uniform(0,1) 中随机生成的值 \(u=0.8413\)，则可以算得\(F_{-1}(u)=1\)，则此次从正态分布中生成的随机数就是 1。

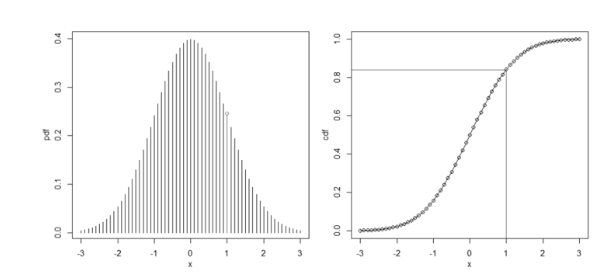
你可能会好奇，面对一个具有复杂表达式的函数， Inverse CDF 方法真的有效吗？来看下面这个例子。假设现在我们希望从下面这个PDF中抽样：

\[f(x)=\left\{\begin{array}{ll}{8 x} & {, \text {if } 0 \leq x<0.25} \\ {\frac{8}{3}-\frac{8}{3} x} & {, \text { if } 0.25 \leq x \leq 1} \\ {0} & {, \text { otherwise }}\end{array}\right. \]

可以算得相应的CDF为

\[F(x)=\left\{\begin{array}{ll}{0} & {, \text { if } x<0} \\ {4 x^{2}} & {, \text { if } 0 \leq x<0.25} \\ {\frac{8}{3} x-\frac{4}{3} x^{2}-\frac{1}{3}} & {, \text { if } 0.25 \leq x \leq 1} \\ {1} & {, \text { if } x>1}\end{array}\right. \]

对于 \(u∈[0,1]\)，它的反函数为:

\[F^{-1}(u)=\left\{\begin{array}{ll}{\frac{\sqrt{u}}{2}} & {, \text { if } 0 \leq u<0.25} \\ {1-\frac{\sqrt{3(1-u)}}{2}} & {, i f 0.25 \leq u \leq 1}\end{array}\right. \]

拒绝采样

我们已经看到 Inverse CDF 方法确实有效。但其实它的缺点也是很明显的，那就是有些分布的 CDF 可能很难通过对 PDF 的积分得到，再或者 CDF 的反函数也很不容易求。这时我们可能需要用到另外一种采样方法，这就是我们即将要介绍的拒绝采样。

下面这张图很好地阐释了拒绝采样的基本思想。假设我们想对 PDF 为 \(p(x)\) 的函数进行采样，但是由于种种原因（例如这个函数很复杂），对其进行采样是相对困难的。但是另外一个 PDF 为 \(q(x)\) 的函数则相对容易采样，例如采用 Inverse CDF 方法可以很容易对对它进行采样，甚至 \(q(x)\) 就是一个均匀分布（别忘了计算机可以直接进行采样的分布就只有均匀分布）。那么，当我们将 \(q(x)\) 与一个常数 MM 相乘之后，可以实现下图所示之关系，即\(M⋅q(x)\) 将 \(p(x)\) 完全“罩住”

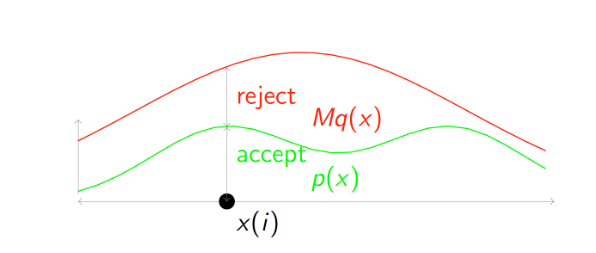
你当然可以采用严密的数学推导来证明Reject Sampling的可行性。但它的原理从直观上来解释也是相当容易理解的。你可以想象一下在上图的例子中，从哪些位置抽出的点会比较容易被接受。显然，红色曲线和绿色曲线所示之函数更加接近的地方接受概率较高，也即是更容易被接受，所以在这样的地方采到的点就会比较多，而在接受概率较低（即两个函数差距较大）的地方采到的点就会比较少，这也就保证了这个方法的有效性。

Reject Sampling方法确实可以解决我们的问题。但是它的一个不足涉及到其采样效率的问题。
最理想的情况下，参考分布应该跟目标分布越接近越好，从图形上来看就是包裹的越紧实越好。但是这种情况的参考分布往往又不那么容易得到。在满足某些条件的时候也确实可以采用所谓的改进方法，即Adaptive Rejection Sampling。

自适应的拒绝采样（Adaptive Rejection Sampling）

前面我们已经分析了，拒绝采样的弱点在于当被拒绝的点很多时，采样的效率会非常不理想。同时我们也支持，如果能够找到一个跟目标分布函数非常接近的参考函数，那么就可以保证被接受的点占大多数（被拒绝的点很少）。这样一来便克服了拒绝采样效率不高的弱点。如果函数是 log-concave 的话，那么我们就可以采样自适应的拒绝采样方法。什么是 log-concave 呢？还是回到我们之前介绍过的 Beta 分布的PDF，我们用下面的代码来绘制 Beta(2, 3) 的函数图像，以及将 Beta(2, 3) 的函数取对数之后的图形

(......更详细的内容看原文)