社会财富分配问题模拟
一个财富分配游戏：
房间里有100个人，每人都有100元钱，他们在玩一个游戏。每轮游戏中，每个人都要拿出一元钱随机给另一个人，最后这100个人的财富分布是怎样的？
研究问题：
1、财富分配模型
模型假设：
① 每个人初始基金100元
② 从18岁到65岁，每天玩一次，简化运算按照一共玩17000轮
③ 每天拿出一元钱，并且随机分配给另一个人
④ 当某人的财富值降到0元时，他在该轮无需拿出1元钱给别人，但仍然有机会得到别人给出的钱
要求：
① 构建模型模拟（这里需要跑17000轮）
② 绘制柱状图，查看该轮财富情况
** 横轴标签代表一个玩家的编号，柱子的高低变动反映该玩家财富值的变化
** 制图分两个情况绘制：不排序绘制、每轮按照财富值排序绘制
** 前100轮，按照每10轮绘制一次柱状图，查看财富变化情况
** 100至1000轮，按照每100轮绘制一次柱状图，查看财富变化情况
** 1000至17000轮，按照每400轮绘制一次柱状图，查看财富变化情况
③ 查看最后财富分配数据是什么分布？
④ 最富有的人相比于初始财富，翻了多少倍？
⑤ 10%的人掌握着多少的财富？30%的人掌握着多少的财富？又有百分之多少人财富缩水至100元以下了？
提示：
① 首先，模拟第一轮游戏分配，不考虑某人财富值降到0元的情况
② 其次，仍然模拟第一轮游戏分配，但考虑某人的财富值降到0元时的情况
③ 构建模型
④ 运行模型，先试运行100条/1000条，再运行17000
⑤ 制图
2、在允许借贷情况下，研究以下问题
和初始模型的区别：
允许借贷意味着可以找亲友、银行、投资人借贷 → 资产为负时，仍然参与游戏
要求：
① 构建模型模拟，再次模拟财富分配情况
** 最富有的人相比于初始财富，翻了多少倍？
** 10%的人掌握着多少的财富？30%的人掌握着多少的财富？又有百分之多少人财富缩水至100元以下了？
② 绘制柱状图，查看该轮财富情况
** 横轴标签代表一个玩家的编号，柱子的高低变动反映该玩家财富值的变化
** 这里只需要每轮按照财富值排序绘制
** 前100轮，按照每10轮绘制一次柱状图，查看财富变化情况
** 100至1000轮，按照每100轮绘制一次柱状图，查看财富变化情况
** 1000至17000轮，按照每400轮绘制一次柱状图，查看财富变化情况
③ 游戏次数与财富分布的标准差的情况，绘图来表示
** 这里用允许借贷情况下模拟的结果
** 横坐标为游戏次数（总共17000次），纵坐标为财富分配标准差
** 绘制折线图
④ 玩家从18岁开始，在经过17年后为35岁，这个期间共进行游戏6200次左右，则此刻查看财富情况，将财富值为负的标记成“破产”，通过图表研究
该类玩家在今后的游戏中能否成功“逆袭”（财富值从负到正为逆袭）、
** 这里绘制柱状图 → 6200至17000轮，按照每500轮绘制一次柱状图
提示：
① 该模型只需要将初始模型中，“财富小于零时无需拿钱给别人”的条件删掉即可
② 最后绘制柱状图时，需要将负债的玩家标红，这里可以通过截取dataframe之后，给与color字段来设置颜色
3、努力的人生会更好吗？
模型假设：
① 每个人初始基金仍为100元
② 一共玩17000轮
③ 每天拿出一元钱，并且随机分配给另一个人
④ 有10个人加倍努力，从而获得了1%的竞争优势
⑤ 允许借贷
允许借贷意味着可以找亲友、银行、投资人借贷 → 资产为负时，仍然参与游戏
要求：
① 构建模型模拟，再次模拟财富分配情况
② 努力的人，最后是否富有？
③ 绘制柱状图，查看该轮财富情况
** 横轴标签代表一个玩家的编号，柱子的高低变动反映该玩家财富值的变化
** 这里只需要每轮按照财富值排序绘制
** 前100轮，按照每10轮绘制一次柱状图，查看财富变化情况
** 100至1000轮，按照每100轮绘制一次柱状图，查看财富变化情况
** 1000至17000轮，按照每400轮绘制一次柱状图，查看财富变化情况
提示：
① 这里设置的10个人id分别为：[1,11,21,31,41,51,61,71,81,91]
② np.random.choice(person_n, p =[...]) → 这里通过设置p来修改概率：努力的10人概率为（1/100.1*1.01），其他人概率为（1/100.1）
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os
import warnings
warnings.filterwarnings('ignore')
# 不发出警告
import time
# 导入时间模块
一个财富分配游戏：
房间里有100个人，每人都有100元钱，他们在玩一个游戏。每轮游戏中，每个人都要拿出一元钱随机给另一个人，最后这100个人的财富分布是怎样的？
1、财富分配模型
模型假设：
① 每个人初始基金100元
② 从18岁到65岁，每天玩一次，简化运算按照一共玩17000轮
③ 每天拿出一元钱，并且随机分配给另一个人
④ 当某人的财富值降到0元时，他在该轮无需拿出1元钱给别人，但仍然有机会得到别人给出的钱
要求：
① 构建模型模拟（这里需要跑17000轮）
② 绘制柱状图，查看该轮财富情况
** 横轴标签代表一个玩家的编号，柱子的高低变动反映该玩家财富值的变化
** 制图分两个情况绘制：不排序绘制、每轮按照财富值排序绘制
** 前100轮，按照每10轮绘制一次柱状图，查看财富变化情况
** 100至1000轮，按照每100轮绘制一次柱状图，查看财富变化情况
** 1000至17000轮，按照每400轮绘制一次柱状图，查看财富变化情况
③ 查看最后财富分配数据是什么分布？
④ 最富有的人相比于初始财富，翻了多少倍？
⑤ 10%的人掌握着多少的财富？30%的人掌握着多少的财富？又有百分之多少人财富缩水至100元以下了？
提示：
① 首先，模拟第一轮游戏分配，不考虑某人财富值降到0元的情况
② 其次，仍然模拟第一轮游戏分配，但考虑某人的财富值降到0元时的情况
③ 构建模型
④ 运行模型，先试运行100条/1000条，再运行17000
⑤ 制图
# 1、财富分配模型测试
# 模型假设：
# ① 每个人初始基金100元
# ② 从18岁到65岁，每天玩一次，简化运算按照一共玩17000天
# ③ 每天拿出一元钱，并且随机分配给另一个人
# ④ 当某人的财富值降到0元时，他在该轮无需拿出1元钱给别人，但仍然有机会得到别人给出的钱
# （1） 模拟第一轮游戏分配
# 先不考虑某人财富值降到0元的情况
person_n = [x for x in range(1,101)]
fortune = pd.DataFrame([100 for i in range(100)], index = person_n)
fortune.index.name = 'id'
# 设定初始参数：游戏玩家100人，起始资金100元
round_r1 = pd.DataFrame({'pre_round':fortune[0],'lost':1})
# 设定第一轮分配财富之前的情况
choice_r1 = pd.Series(np.random.choice(person_n,100))
gain_r1 = pd.DataFrame({'gain':choice_r1.value_counts()})
# 这一轮中每个人随机指定给“谁”1元钱，并汇总这一轮每个人的盈利情况
round_r1 = round_r1.join(gain_r1)
round_r1.fillna(0,inplace = True)
fortune[1] = round_r1['pre_round'] - round_r1['lost'] + round_r1['gain']
# 合并数据，得到这一轮每个人“盈亏”多少钱 → 得到这一轮财富分配的结果
fortune.head()
# （2） 模拟第一轮游戏分配
# 考虑情况：当某人的财富值降到0元时，他在该轮无需拿出1元钱给别人，但仍然有机会得到别人给出的钱
person_n = [x for x in range(1,101)]
fortune = pd.DataFrame([100 for i in range(100)], index = person_n)
fortune.index.name = 'id'
# 设定初始参数：游戏玩家100人，起始资金100元
round_r1 = pd.DataFrame({'pre_round':fortune[0],'lost':0})
round_r1['lost'][round_r1['pre_round'] > 0] = 1
# 设定第一轮分配财富之前的情况 → 该轮财富值为0的不需要拿钱给别人
round_players = round_r1[round_r1['pre_round'] > 0]
# 筛选出参与游戏的玩家：财富值>0
choice_r1 = pd.Series(np.random.choice(person_n,len(round_players)))
gain_r1 = pd.DataFrame({'gain':choice_r1.value_counts()})
# 这一轮中每个人随机指定给“谁”1元钱，并汇总这一轮每个人的盈利情况
round_r1 = round_r1.join(gain_r1)
round_r1.fillna(0,inplace = True)
fortune[1] = round_r1['pre_round'] - round_r1['lost'] + round_r1['gain']
# 合并数据，得到这一轮财富分配的结果
fortune.head()
# （3）构建函数模型
# 这里注意：当某人的财富值降到0元时，他在该轮无需拿出1元钱给别人，但仍然有机会得到别人给出的钱
def game1(data, roundi):
if len(data[data[roundi - 1] ==0]) > 0:
# 当数据包含财富值为0的玩家时
round_i = pd.DataFrame({'pre_round':data[roundi-1],'lost':0})
con = round_i['pre_round'] > 0
round_i['lost'][con] = 1 # 设定每轮分配财富之前的情况 → 该轮财富值为0的不需要拿钱给别人
round_players_i = round_i[con] # 筛选出参与游戏的玩家：财富值>0
choice_i = pd.Series(np.random.choice(person_n,len(round_players_i)))
gain_i = pd.DataFrame({'gain':choice_i.value_counts()}) # 这一轮中每个人随机指定给“谁”1元钱，并汇总这一轮每个人的盈利情况
round_i = round_i.join(gain_i)
round_i.fillna(0,inplace = True)
return round_i['pre_round'] - round_i['lost'] + round_i['gain']
# 合并数据，得到这一轮财富分配的结果
else:
# 当数据不包含财富值为0的玩家时
round_i = pd.DataFrame({'pre_round':data[roundi-1],'lost':1}) # 设定每轮分配财富之前的情况
choice_i = pd.Series(np.random.choice(person_n,100))
gain_i = pd.DataFrame({'gain':choice_i.value_counts()}) # 这一轮中每个人随机指定给“谁”1元钱，并汇总这一轮每个人的盈利情况
round_i = round_i.join(gain_i)
round_i.fillna(0,inplace = True)
return round_i['pre_round'] - round_i['lost'] + round_i['gain']
# 合并数据，得到这一轮财富分配的结果
print('finished!')
# （4）运行模型，模拟财富分配
person_n = [x for x in range(1,101)]
fortune = pd.DataFrame([100 for i in range(100)], index = person_n)
fortune.index.name = 'id'
# 设定初始参数：游戏玩家100人，起始资金100元
starttime = time.time() # 模型开始时间
for round in range(1,17001):
fortune[round] = game1(fortune,round) # 进行17000轮随机分配模拟
game1_result = fortune.T # 转置后得到结果数据 → 列为每一个人的id，行为每一轮的财富分配结果
endtime = time.time() # 模型结束时间
print('模型总共用时%i秒' % (endtime - starttime))
# 计算时间
game1_result.tail()
# 查看最后5条数据
# （5）绘制柱状图
# ** 前100轮，按照每10轮绘制一次柱状图，查看财富变化情况
# ** 100至1000轮，按照每100轮绘制一次柱状图，查看财富变化情况
# ** 1000至17000轮，按照每400轮绘制一次柱状图，查看财富变化情况
# ① 不排序绘制
os.chdir('C:\\Users\\Hjx\\Desktop\\项目13社会财富分配问题模拟\\财富分配模型_初始模型_不排序绘制\\')
def graph1(data,start,end,length):
for n in list(range(start,end,length)):
datai = data.iloc[n]
plt.figure(figsize = (10,6))
plt.bar(datai.index,datai.values,color='gray',alpha = 0.8,width = 0.9)
plt.ylim((0,400))
plt.xlim((-10,110))
plt.title('Round %d' % n)
plt.xlabel('PlayerID')
plt.ylabel('Fortune')
plt.grid(color='gray', linestyle='--', linewidth=0.5)
plt.savefig('graph1_round_%d.png' % n, dpi=200)
# 创建绘图函数1
graph1(game1_result,0,100,10)
graph1(game1_result,100,1000,100)
graph1(game1_result,1000,17400,400)
print('finished!')
# 一些结论
round_17000_1 = pd.DataFrame({'money':game1_result.iloc[17000]}).sort_values(by = 'money',ascending = False).reset_index()
round_17000_1['fortune_pre'] = round_17000_1['money'] / round_17000_1['money'].sum()
round_17000_1['fortune_cumsum'] = round_17000_1['fortune_pre'].cumsum()
round_17000_1.head()
# 最后一轮中，最富有的人财富值为365元，相比于初始财富，翻了3.65倍
# 10%的人掌握着28%的财富，20%的人掌握着51%的财富？
# 60%的人财富缩水至100元以下了？
2、在允许借贷情况下，研究以下问题
和初始模型的区别：
允许借贷意味着可以找亲友、银行、投资人借贷 → 资产为负时，仍然参与游戏
要求：
① 构建模型模拟，再次模拟财富分配情况
** 最富有的人相比于初始财富，翻了多少倍？
** 10%的人掌握着多少的财富？30%的人掌握着多少的财富？又有百分之多少人财富缩水至100元以下了？
② 绘制柱状图，查看该轮财富情况
** 横轴标签代表一个玩家的编号，柱子的高低变动反映该玩家财富值的变化
** 这里只需要每轮按照财富值排序绘制
** 前100轮，按照每10轮绘制一次柱状图，查看财富变化情况
** 100至1000轮，按照每100轮绘制一次柱状图，查看财富变化情况
** 1000至17000轮，按照每400轮绘制一次柱状图，查看财富变化情况
③ 游戏次数与财富分布的标准差的情况，绘图来表示
** 这里用允许借贷情况下模拟的结果
** 横坐标为游戏次数（总共17000次），纵坐标为财富分配标准差
** 绘制折线图
④ 玩家从18岁开始，在经过17年后为35岁，这个期间共进行游戏6200次左右，则此刻查看财富情况，将财富值为负的标记成“破产”，通过图表研究
该类玩家在今后的游戏中能否成功“逆袭”（财富值从负到正为逆袭）、
** 这里绘制柱状图 → 6200至17000轮，按照每500轮绘制一次柱状图
提示：
① 该模型只需要将初始模型中，“财富小于零时无需拿钱给别人”的条件删掉即可
② 最后绘制柱状图时，需要将负债的玩家标红，这里可以通过截取dataframe之后，给与color字段来设置颜色
（1）构建函数模型
# 这里注意：当某人的财富值降到0元时，他在该轮无需拿出1元钱给别人，但仍然有机会得到别人给出的钱
def game2(data, roundi):
round_i = pd.DataFrame({'pre_round':data[roundi-1],'lost':1}) # 设定每轮分配财富之前的情况
choice_i = pd.Series(np.random.choice(person_n,100))
gain_i = pd.DataFrame({'gain':choice_i.value_counts()}) # 这一轮中每个人随机指定给“谁”1元钱，并汇总这一轮每个人的盈利情况
round_i = round_i.join(gain_i)
round_i.fillna(0,inplace = True)
return round_i['pre_round'] - round_i['lost'] + round_i['gain']
# 合并数据，得到这一轮财富分配的结果
print('finished!')
# （2）运行模型，模拟财富分配
person_n = [x for x in range(1,101)]
fortune = pd.DataFrame([100 for i in range(100)], index = person_n)
fortune.index.name = 'id'
# 设定初始参数：游戏玩家100人，起始资金100元
starttime = time.time() # 模型开始时间
for round in range(1,17001):
fortune[round] = game2(fortune,round) # 进行17000轮随机分配模拟
game2_result = fortune.T # 转置后得到结果数据 → 列为每一个人的id，行为每一轮的财富分配结果
endtime = time.time() # 模型结束时间
print('模型总共用时%i秒' % (endtime - starttime))
# 计算时间
game2_result.tail()
# 查看最后5条数据
# 一些结论
round_17000_2 = pd.DataFrame({'money':game2_result.iloc[17000]}).sort_values(by = 'money',ascending = False).reset_index()
round_17000_2['fortune_pre'] = round_17000_2['money'] / round_17000_2['money'].sum()
round_17000_2['fortune_cumsum'] = round_17000_2['fortune_pre'].cumsum()
round_17000_2.head()
# 最后一轮中，最富有的人财富值为458元，相比于初始财富，翻了4.58倍
# 10%的人掌握着33%的财富，20%的人掌握着59%的财富？
# 50%的人财富缩水至100元以下了？
# （3）游戏次数与财富分布的标准差的情况，绘图来表示
os.chdir('C:\\Users\\Hjx\\Desktop\\项目13社会财富分配问题模拟\\财富分配模型_允许借贷\\')
def graph3(data,start,end,length):
for n in list(range(start,end,length)):
datai = data.iloc[n].sort_values().reset_index()[n]
plt.figure(figsize = (10,6))
plt.bar(datai.index,datai.values,color='gray',alpha = 0.8,width = 0.9)
plt.grid(color='gray', linestyle='--', linewidth=0.5)
plt.ylim((-200,400))
plt.xlim((-10,110))
plt.title('Round %d' % n)
plt.xlabel('PlayerID')
plt.ylabel('Fortune')
plt.savefig('graph3_round_%d.png' % n, dpi=200)
# 创建绘图函数2
graph3(game2_result,0,100,10)
graph3(game2_result,100,1000,100)
graph3(game2_result,1000,17400,400)
print('finished!')
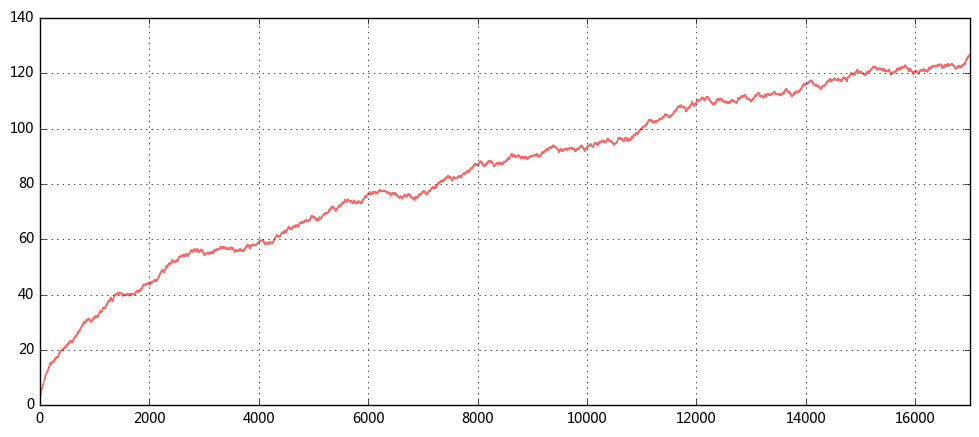
# （4）游戏次数与财富分布的标准差的情况，绘图来表示
game2_st = game2_result.std(axis = 1)
game2_st.plot(figsize = (12,5),color = 'red',alpha = 0.6,grid = True)
plt.show()
# 游戏早期前2000轮的标准差变动最为激烈；
# 而在6000-6500轮游戏后，标准差的变化趋于平缓，但仍在上升；
# 按照我们设定的游戏与人生的对应规则，这时玩家年龄为35岁
# （5）玩家从18岁开始，在经过17年后为35岁，这个期间共进行游戏6200次左右，则此刻查看财富情况，将财富值为负的标记成“破产
# 通过图表研究该类玩家在今后的游戏中能否成功“逆袭”（财富值从负到正为逆袭）、
# 这里绘制折线图
game2_round6200 = pd.DataFrame({'money':game2_result.iloc[6200].sort_values().reset_index()[6200],
'id':game2_result.iloc[6200].sort_values().reset_index()['id'],
'color':'gray'})
game2_round6200['color'][game2_round6200['money'] < 0] = 'red'
id_pc = game2_round6200['id'][game2_round6200['money'] < 0].tolist()
print('财富值为负的玩家id为：\n',id_pc)
# 筛选数据
# 设置颜色参数
plt.figure(figsize = (10,6))
plt.bar(game2_round6200.index,game2_round6200['money'],color = game2_round6200['color'],alpha = 0.8,width = 0.9)
plt.grid(color='gray', linestyle='--', linewidth=0.5)
plt.ylim((-200,400))
plt.xlim((-10,110))
plt.title('Round 6200')
plt.xlabel('PlayerID')
plt.ylabel('Fortune')
plt.show()
# 绘制柱状图
# 绘图分析
os.chdir('C:\\Users\\Hjx\\Desktop\\项目13社会财富分配问题模拟\\财富分配模型_允许借贷_负债玩家逆袭\\')
def graph4(data,start,end,length):
for n in list(range(start,end,length)):
datai = pd.DataFrame({'money':data.iloc[n],'color':'gray'})
datai['color'].loc[id_pc] = 'red'
datai = datai.sort_values(by = 'money').reset_index()
plt.figure(figsize = (10,6))
plt.bar(datai.index,datai['money'],color=datai['color'],alpha = 0.8,width = 0.9)
plt.grid(color='gray', linestyle='--', linewidth=0.5)
plt.ylim((-200,400))
plt.xlim((-10,110))
plt.title('Round %d' % n)
plt.xlabel('PlayerID')
plt.ylabel('Fortune')
plt.savefig('graph4_round_%d.png' % n, dpi=200)
# 创建绘图函数2
graph4(game2_result,6200,17000,500)
print('finished!')
# 结论
# 以35岁为界，虽然破产以后，不足一半的概率回复到普通人的生活，但想要逆袭暴富，却是相当困难的
3、努力的人生会更好吗？
模型假设：
① 每个人初始基金仍为100元
② 一共玩17000轮
③ 每天拿出一元钱，并且随机分配给另一个人
④ 有10个人加倍努力，从而获得了1%的竞争优势
⑤ 允许借贷
允许借贷意味着可以找亲友、银行、投资人借贷 → 资产为负时，仍然参与游戏
要求：
① 构建模型模拟，再次模拟财富分配情况
② 努力的人，最后是否富有？
③ 绘制柱状图，查看该轮财富情况
** 横轴标签代表一个玩家的编号，柱子的高低变动反映该玩家财富值的变化
** 这里只需要每轮按照财富值排序绘制
** 前100轮，按照每10轮绘制一次柱状图，查看财富变化情况
** 100至1000轮，按照每100轮绘制一次柱状图，查看财富变化情况
** 1000至17000轮，按照每400轮绘制一次柱状图，查看财富变化情况
提示：
① 这里设置的10个人id分别为：[1,11,21,31,41,51,61,71,81,91]
② np.random.choice(person_n, p =[...]) → 这里通过设置p来修改概率：努力的10人概率为0.0101，其他人概率为（0.899/90）
# （1）构建函数模型
# 这里注意：当某人的财富值降到0元时，他在该轮无需拿出1元钱给别人，但仍然有机会得到别人给出的钱
person_p = [0.899/90 for i in range(100)]
for i in [1,11,21,31,41,51,61,71,81,91]:
person_p[i-1] = 0.0101
# 设置概率
def game3(data, roundi):
round_i = pd.DataFrame({'pre_round':data[roundi-1],'lost':1}) # 设定每轮分配财富之前的情况
choice_i = pd.Series(np.random.choice(person_n,100, p = person_p))
gain_i = pd.DataFrame({'gain':choice_i.value_counts()}) # 这一轮中每个人随机指定给“谁”1元钱，并汇总这一轮每个人的盈利情况
round_i = round_i.join(gain_i)
round_i.fillna(0,inplace = True)
return round_i['pre_round'] - round_i['lost'] + round_i['gain']
# 合并数据，得到这一轮财富分配的结果
print('finished!')
# （2）运行模型，模拟财富分配
person_n = [x for x in range(1,101)]
fortune = pd.DataFrame([100 for i in range(100)], index = person_n)
fortune.index.name = 'id'
# 设定初始参数：游戏玩家100人，起始资金100元
starttime = time.time() # 模型开始时间
for round in range(1,17001):
fortune[round] = game3(fortune,round) # 进行17000轮随机分配模拟
game3_result = fortune.T # 转置后得到结果数据 → 列为每一个人的id，行为每一轮的财富分配结果
endtime = time.time() # 模型结束时间
print('模型总共用时%i秒' % (endtime - starttime))
# 计算时间
game3_result.tail()
# 查看最后5条数据
# 绘图分析
os.chdir('C:\\Users\\Hjx\\Desktop\\项目13社会财富分配问题模拟\\财富分配模型_努力人生\\')
plt.figure(figsize = (10,6))
data0 = pd.DataFrame({'money':game3_result.iloc[0],'color':'gray'})
data0['color'].loc[[1,11,21,31,41,51,61,71,81,91]] = 'red'
plt.bar(data0.index,data0['money'],color=data0['color'],alpha = 0.8,width = 0.9)
plt.grid(color='gray', linestyle='--', linewidth=0.5)
plt.ylim((-200,400))
plt.xlim((-10,110))
plt.title('Round %d' % 0)
plt.xlabel('PlayerID')
plt.ylabel('Fortune')
plt.savefig('graph5_round_%d.png' % 0, dpi=200)
# 绘制起始图片
def graph5(data,start,end,length):
for n in list(range(start,end,length)):
datai = pd.DataFrame({'money':data.iloc[n],'color':'gray'})
datai['color'].loc[[1,11,21,31,41,51,61,71,81,91]] = 'red'
datai = datai.sort_values(by = 'money').reset_index()
plt.figure(figsize = (10,6))
plt.bar(datai.index,datai['money'],color=datai['color'],alpha = 0.8,width = 0.9)
plt.grid(color='gray', linestyle='--', linewidth=0.5)
plt.ylim((-200,400))
plt.xlim((-10,110))
plt.title('Round %d' % n)
plt.xlabel('PlayerID')
plt.ylabel('Fortune')
plt.savefig('graph5_round_%d.png' % n, dpi=200)
# 创建绘图函数2
graph5(game3_result,10,100,10)
graph5(game3_result,100,1000,100)
graph5(game3_result,1000,17400,400)
print('finished!')
# 结论
# 社会财富的总体分布形态没有什么变化
# 10位努力玩家中多位都进入了富人top20！
