房价影响因素挖掘

 房价影响因素挖掘

 

1、数据清洗、整合
① 将“house_rent”、“house_sell”分别读取
② 分别计算平方米建筑面积的月租金、每平方米建筑面积的房价
③ 将数据按照小区名合并
====>>>
① 删除缺失值
② 按照小区做均值分析

 

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

import warnings
warnings.filterwarnings('ignore') 
# 不发出警告

'''
(1)读取数据
'''

import os
os.chdir(r'C:\Users\Administrator\Desktop\python数据分析\项目\10房价')
# 创建工作路径

df01 = pd.read_csv('house_rent.csv',engine = 'python')
df02 = pd.read_csv('house_sell.csv',engine = 'python')
# 读取数据

df01.dropna(inplace = True)
df02.dropna(inplace = True)
# 删除缺失值

'''
(2)计算指标并按照租金、售价汇总
'''
df01['rent_area'] = df01['price']/df01['area']
data_rent = df01[['community','rent_area','lng','lat']].groupby(by = 'community').mean()
data_sell = df02[['property_name','average_price','lng','lat']].groupby(by = 'property_name').mean()
data_rent.reset_index(inplace = True)
data_sell.reset_index(inplace = True)
#数据计算并汇总

data = pd.merge(data_rent,data_sell,left_on ='community',right_on='property_name')
data = data[['community','rent_area','average_price','lng_x','lat_x']]
data.rename(columns={'average_price':'sell_area', 'lng_x':'lng', 'lat_x':'lat'}, inplace = True)  # 调整列名

 

房屋的租售比一般 200--300的区别比较合适

比如100平方米的房子，均价2万，总共200万；

假如贷款 3成，即600000万，按照6%左右的利率去算，贷款140万，期限30年； 用贷款计算器算下：

140万贷款30年，6.37%利率，本息合计3142656.29，每月还款8729.6元；租金跑赢每月的还款8729.6，租金假如是8800，

租售比8800/100/20000=0.0044     1/0.0044=227.27；假如你买的房子能跑赢汇率，大概在200--300之间。如果在这个区间内，或者小于200则是非常有投资价值的。

如果大于200，甚至超过500，则可能存在泡沫风险。

 

'''
(3)计算房屋租售比
'''
# 计算“房屋售租比”，并做初步判断
# “房屋售租比”=“每平方米建筑面积的房价”/“每平方米建筑面积的月租金” 
# 含义可以简单理解为：“在保持当前的房价和租金条件不变的情况下，完全收回投资需要多少个月？”
#  **一般而言，按照国际经验，在一个房产运行情况良好的区域，应该可以在200-300个月内完全回收投资。
#  **如果少于200个月（17年）就能收回投资，说明这个地区有较高的投资价值；
#  **如果一个地区需要高于300个月（25年），比如1200个月（100年）才能回收投资，则说明该地区有潜在的房产泡沫风险。

data['sell_rent'] = data['sell_area']/data['rent_area']
print('上海房屋租售比中位数为%i个月' % data['sell_rent'].median())
# 计算售租比，及中位数


# 绘制直方图
data['sell_rent'].plot.hist(stacked=True,bins=100,color = 'green',alpha=0.5,grid=True,figsize = (10,4))
plt.title('房屋售租比-直方图')

# 绘制箱型图
color = dict(boxes='DarkGreen', whiskers='DarkOrange', medians='DarkBlue', caps='Gray')
data['sell_rent'].plot.box(vert=False, grid = True,color = color,figsize = (10,4)) 
plt.title('房屋售租比-箱型图')

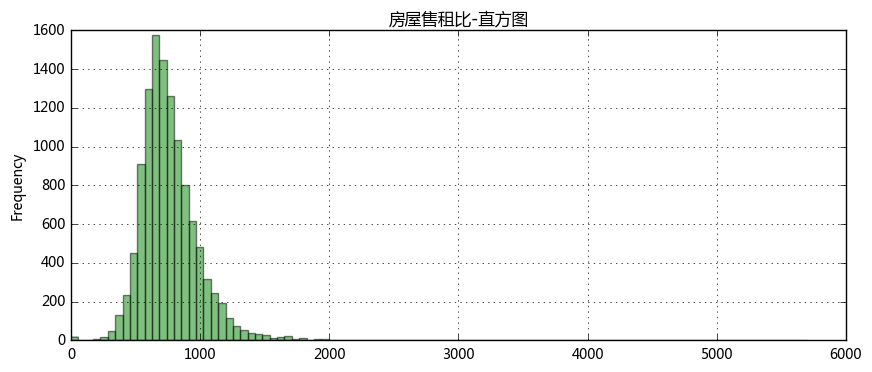
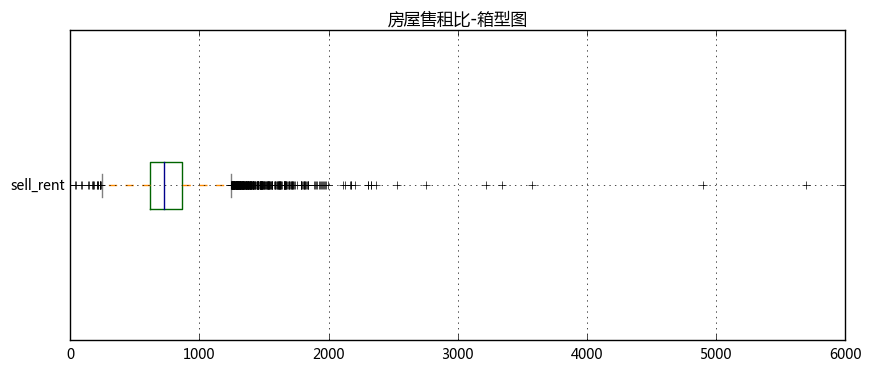
一个尴尬的结论
如果按照中位数725个月来看，假设从25岁研究生一毕业，就立刻全款买了一套房，然后放出去收租
 那么约85岁时，这60年来陆陆续续所收的租金总数就可以达到了25岁时买房所付的钱啦
**这里还没考虑净现值折算问题
 ① 如果仅靠租金收入的话，上海全市平均回收投资需要725个月。而这种格局的维持，必须有赖于购房者对上海的房价上升的持续预期。
 也就是说，在上海，投资房产绝不是利率收益，而是预期收益（其实城市越小租金回报反而越高）
 ② 上海不是这么看住房投资的（绝大多数房子房租收入跑不赢商贷利率，否则按照这个思路看那肯定是买一个亏一个）

 

 

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

import warnings
warnings.filterwarnings('ignore') 
# 不发出警告


'''
(1)导出数据
'''

data.to_csv('pro10data.csv')


print('finish')

 

上海市人口密度、路网密度、餐饮价格和“房屋每平米均价”是否有关系呢？

上海市人口密度、路网密度、餐饮价格和“房屋每平米均价”是否有关系呢？
要求：
① 首先，导出整理好的数据，并qgis中绘制空间格网图，查看房屋每平米均价、房屋每平米租金及售租比数据的空间分布
② 第二，空间统计，分别按照格网对人口密度、路网密度、餐饮价格进行指标统计并标准化
③ 第三，加载上海中心点point空间数据，计算每个网格到市中心距离
④ 第四，将空间格网的“房屋每平米均价”按照距市中心的距离排序，并制作散点图，看看能否挖掘出什么信息
   *** 这里市中心点坐标为：lng-353508.848122，lat-3456140.926976 (投影坐标系)
提示：
① 导出csv数据，用dataframe.to_csv()
② qgis加载数据后，以“net_population”为格网数据做空间统计
③ 注意qgis数据都为投影坐标系
④ 人口密度指标 → 已有“net_population”数据
   路网密度指标 → 以格网为空间单元，计算道路长度
   餐饮价格指标 → 以格网为空间单元，计算餐饮设施的人均均价数据
   *** 最后数据导入python中，标准化得分至0-1区间
   *** 导入数据后要填充空值为0
   *** qgis中可以用结果net数据作为下一个分析数据，以此将统计结果汇总在一张属性表内
   *** 格网数据在导出前，先转为点数据，并计算经纬度，这里用投影经纬度，好依据中心点坐标计算离市中心距离
⑤ 清洗数据，去除“售租比”为0的数据

 

都转成投影坐标系 ===>>图层转成投影坐标系

 人口的指标已经有了net_polulation

路网密度指标：Z值 

矢量--分析工具---计算线条总长度

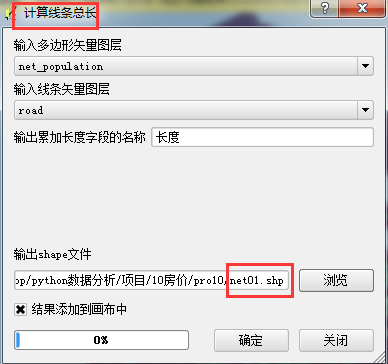
餐饮的价格指标

计算多边形内点的数目

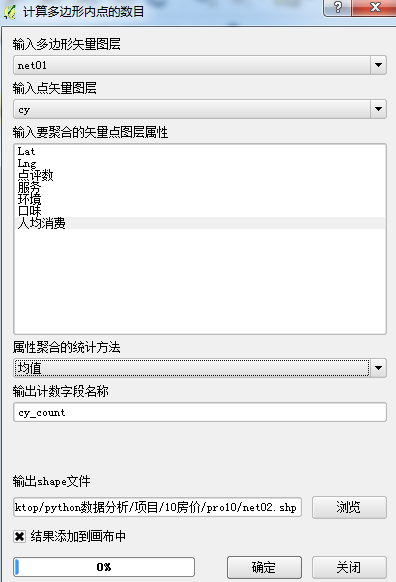
每个单元格内小区里边租金的均值和房价的均值

datapoin是pro10data的投影坐标系

 

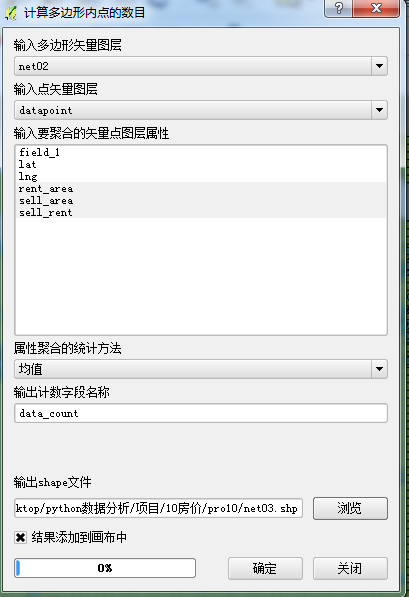
得到net03数据，分别按照不同的指标进行核算，先按照房价sell_area

加载上海市行政区数据，设置下样式

 

 

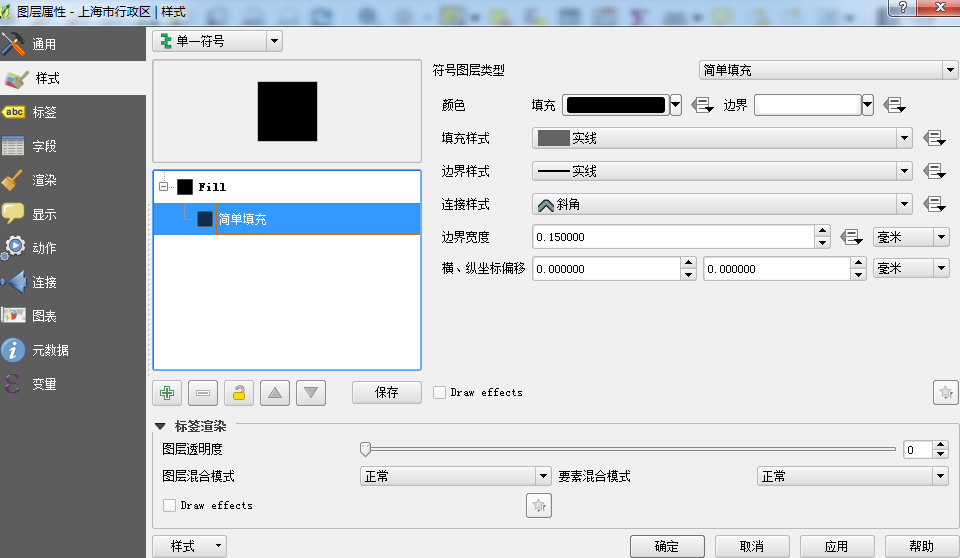
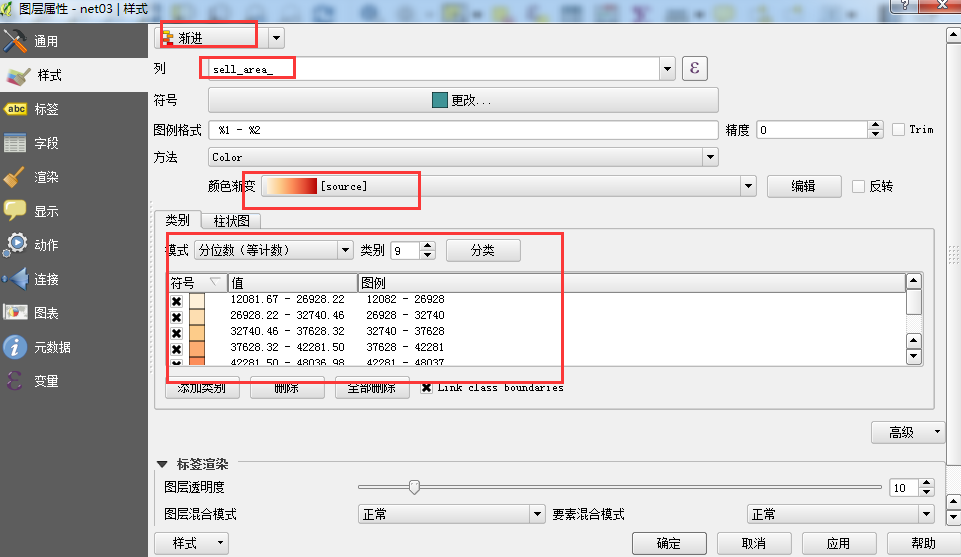
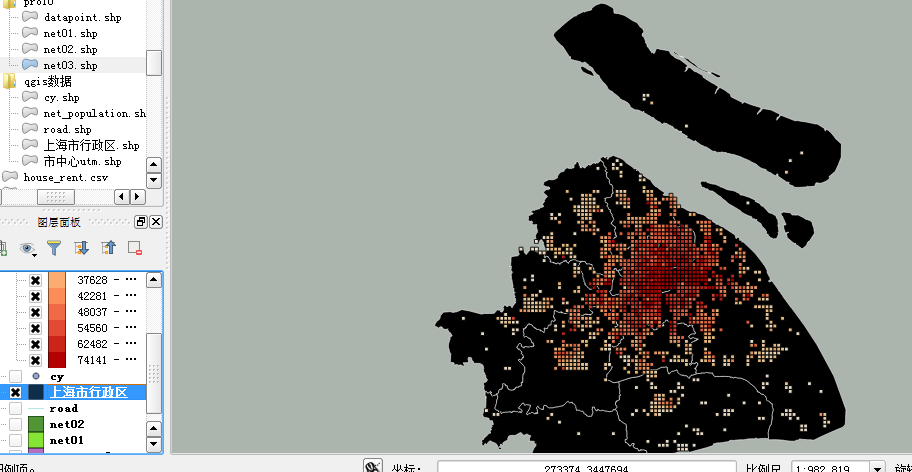
再看看它的租金水平：rent_area

 

离市中心的距离，只要算出格网点就可以了

把栅格从网格变成点

 矢量--几何工具--导出多边形的点（质心）  得到netpoint，就不把它做投影了，需要的就是它的投影坐标系的点坐标

 添加X、Y坐标，

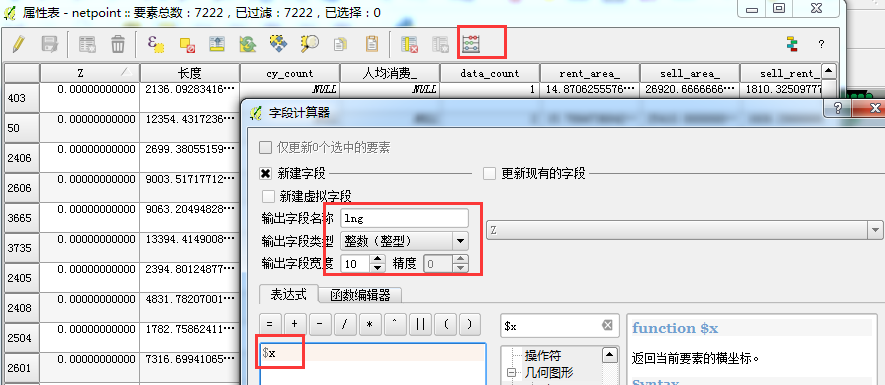
同理lat

得到：

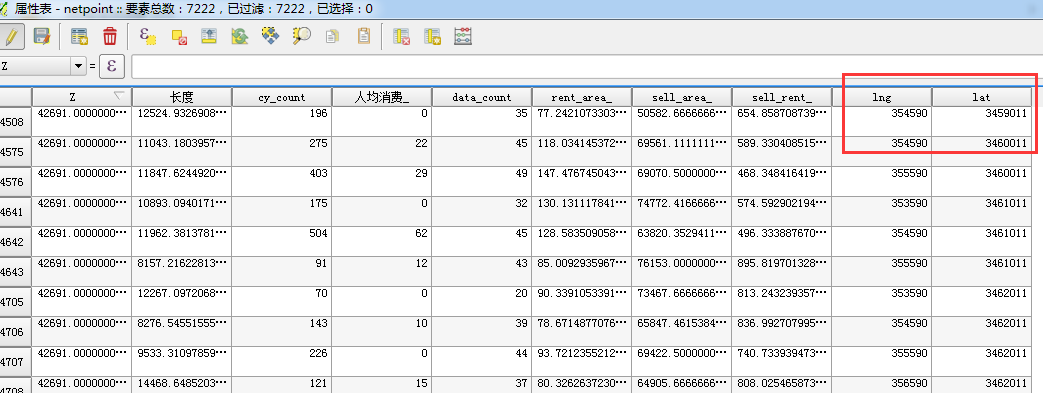
 导出得到result02.xlsx的数据

 

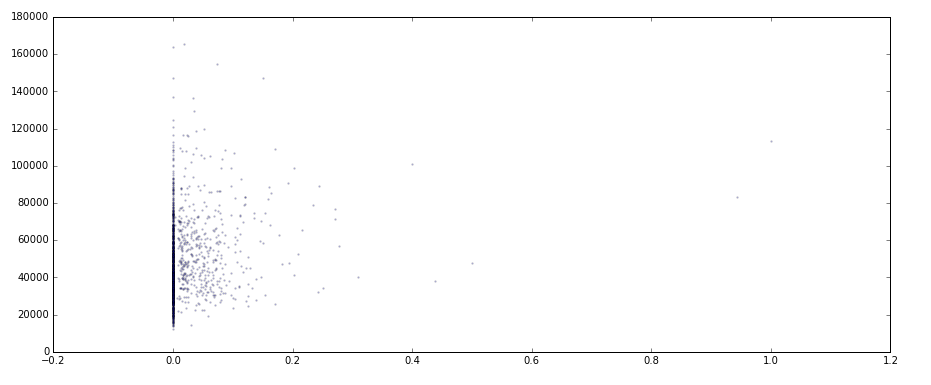
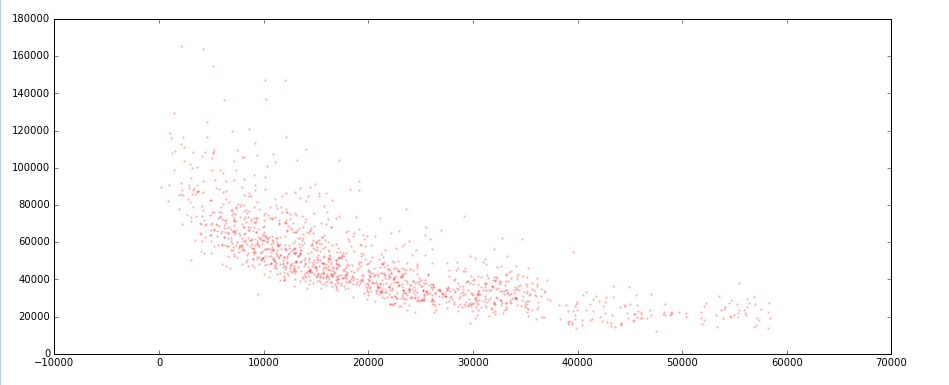
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

import warnings
warnings.filterwarnings('ignore') 
# 不发出警告


'''
(1)导出数据
'''

data.to_csv('pro10data.csv')
'''
(2)加载数据
'''
data_q3 = pd.read_csv(r'C:\Users\Administrator\Desktop\python数据分析\项目\10房价\result02.csv',engine = 'python')
data_q3.fillna(0,inplace = True)


'''
(3)指标标准化处理
'''
def f1(data,col):
    return (data[col]-data[col].min())/(data[col].max()-data[col].min())
# 创建函数

data_q3['人口密度指标'] = f1(data_q3,'Z')
data_q3['路网密度指标'] = f1(data_q3,'长度')
data_q3['餐饮价格指标'] = f1(data_q3,'人均消费_')
# 指标标准化

data_q3['离市中心距离'] = ((data_q3['lng'] - 353508.848122)**2 + (data_q3['lat']-3456140.926976)**2)**0.5
# 计算市中心距离

data_q3_test = data_q3[['人口密度指标','路网密度指标','餐饮价格指标','sell_area_','离市中心距离']]
data_q3_test = data_q3_test[data_q3_test['sell_area_']>0].reset_index()
del data_q3_test['index']
# 清洗数据，去除“房屋每平米均价”为0的数据

#查看整个指标相关性
plt.figure(figsize = (15, 6))
plt.scatter(data_q3_test['人口密度指标'],data_q3_test['sell_area_'],s = 2,alpha = 0.2)
plt.figure(figsize = (15, 6))
plt.scatter(data_q3_test['路网密度指标'],data_q3_test['sell_area_'],s = 2,alpha = 0.2)
plt.figure(figsize = (15, 6))
plt.scatter(data_q3_test['餐饮价格指标'],data_q3_test['sell_area_'],s = 2,alpha = 0.2)
plt.figure(figsize = (15, 6))
plt.scatter(data_q3_test['离市中心距离'],data_q3_test['sell_area_'],color = 'red',s = 2,alpha = 0.2)

data_q3_test.corr().loc['sell_area_']  #查看指标之间相关系数

print('finish')

 

 

 

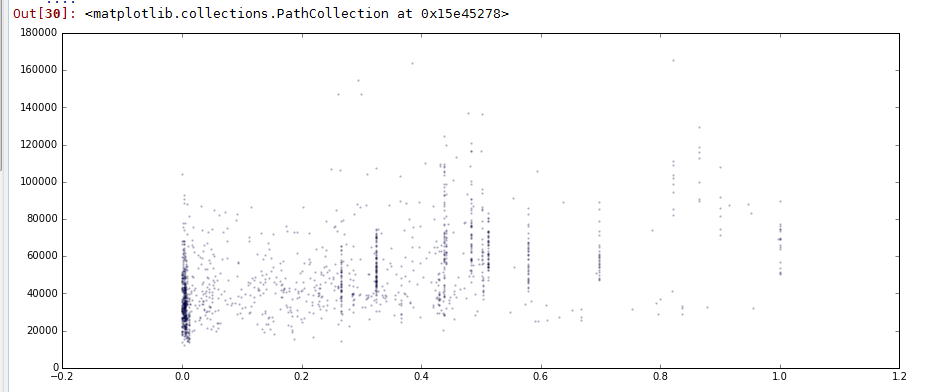
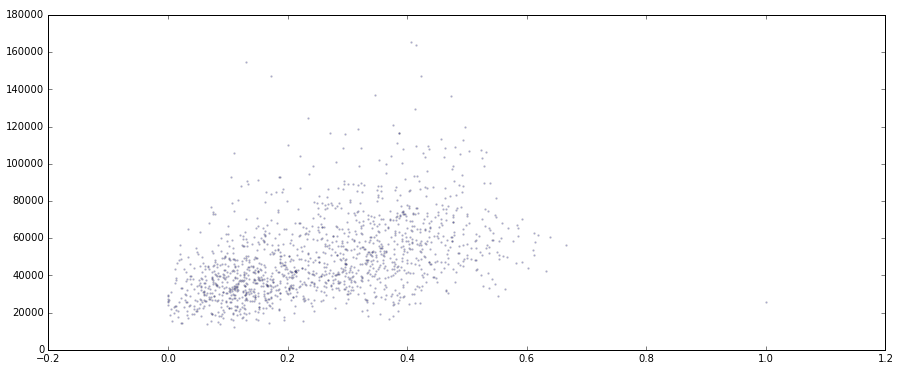
# 结论
① 在上海全市层面，“离市中心距离”与“房屋每平米均价”相关性最强
② “人口密度”及“路网密度”和“房屋每平米均价”为中等相关
③ “餐饮价格”与“房屋每平米均价”为弱相关
 ④ “房屋每平米均价”数据的离散程度却和空间距离有关 → “房屋每平米均价”越靠近市中心越离散，越远离市中心则越收敛

 

 

按照离市中心距离每10km，分别再次判断人口密度、路网密度、餐饮价格和“房屋每平米均价”的相关程度

按照离市中心距离每10km，分别再次判断人口密度、路网密度、餐饮价格和“房屋每平米均价”的相关程度
要求：
① 按照空间距离分别迭代计算三指标和“房屋每平米均价”的关系
② 绘制折线图查看：随着市中心距离增加，不同指标相关系系数变化情况
   *** 用bokeh制图
====>>>
① 用for循环迭代空间距离，然后筛选数据并计算相关性
② bokeh可以通过多次调用figure.line()来绘制多条折线图

 

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

import warnings
warnings.filterwarnings('ignore') 
# 不发出警告
'''
# 按照空间距离分别迭代计算三指标和“房屋每平米均价”的关系
(1)按照市中心距离来分析指标相关性
'''
dis = []                # 距离空列表
rkmd_pearson = []       # 人口密度相关性系数空列表
lwmd_pearson = []       # 路网密度相关性系数空列表
cyjg_pearson = []       # 餐饮价格相关性系数空列表
zxjl_pearson = []       # 中心距离相关性系数空列表

for distance in range(10000,70000,10000):
    datai = data_q3_test[data_q3_test['离市中心距离'] <= distance]
    r_value = datai.corr().loc['sell_area_']
    # 筛选数据并计算相关系数
    dis.append(distance)
    rkmd_pearson.append(r_value.loc['人口密度指标'])
    lwmd_pearson.append(r_value.loc['路网密度指标'])
    cyjg_pearson.append(r_value.loc['餐饮价格指标'])
    zxjl_pearson.append(r_value.loc['离市中心距离'])
    # 添加列表值
    print('离市中心距离小于等于%i米：' % distance)
    print('数据量为%i条' % len(datai))
    print('人口密度与房屋每平米均价的相关系数为：%.3f' % r_value.loc['人口密度指标'])
    print('路网密度与房屋每平米均价的相关系数为：%.3f' % r_value.loc['路网密度指标'])
    print('餐饮价格与房屋每平米均价的相关系数为：%.3f' % r_value.loc['餐饮价格指标'])
    print('离市中心距离与房屋每平米均价的相关系数为：%.3f' % r_value.loc['离市中心距离'])
    print('-------\n')

'''
(2)折线图绘制
'''
# 绘制折线图查看：随着市中心距离增加，不同指标相关性系数变化情况

from bokeh.models import HoverTool

from bokeh.plotting import figure,show,output_file
from bokeh.models import ColumnDataSource


df_r = pd.DataFrame({'rkmd_pearson':rkmd_pearson,
                    'lwmd_pearson':lwmd_pearson,
                    'cyjg_pearson':cyjg_pearson,
                    'zxjl_pearson':zxjl_pearson},
                   index = dis)
source = ColumnDataSource(data=df_r)
# 创建数据

hover = HoverTool(tooltips=[("离市中心距离", "@index"),
                           ("人口密度相关系数", "@rkmd_pearson"),
                           ("道路密度相关系数", "@lwmd_pearson"),
                           ("餐饮价格相关系数", "@cyjg_pearson"),
                           ("中心距离相关系数", "@zxjl_pearson"),])  
# 设置标签显示内容

output_file(r'C:\Users\Administrator\Desktop\python数据分析\项目\10房价\pro1001.html')
p = figure(plot_width=900, plot_height=350, title="随着市中心距离增加，不同指标相关性系数变化情况",
          tools=[hover,'box_select,reset,xwheel_zoom,pan,crosshair'])
# 构建绘图空间
p.line(x='index',y='rkmd_pearson',source = source,line_alpha = 0.8, line_color = 'green',line_dash = [15,4],legend="人口密度相关系数") 
p.circle(x='index',y='rkmd_pearson',source = source, size = 8,color = 'green',alpha = 0.8,legend="人口密度相关系数")

# 绘制折线图1
p.line(x='index',y='lwmd_pearson',source = source,line_alpha = 0.8, line_color = 'blue',line_dash = [15,4],legend="道路密度相关系数") 
p.circle(x='index',y='lwmd_pearson',source = source, size = 8,color = 'blue',alpha = 0.8,legend="道路密度相关系数")
# 绘制折线图2
p.line(x='index',y='cyjg_pearson',source = source,line_alpha = 0.8, line_color = 'black',line_dash = [15,4],legend="餐饮价格相关系数") 
p.circle(x='index',y='cyjg_pearson',source = source, size = 8,color = 'black',alpha = 0.8,legend="餐饮价格相关系数")
# 绘制折线图3
p.line(x='index',y='zxjl_pearson',source = source,line_alpha = 0.8, line_color = 'red',line_dash = [15,4],legend="中心距离相关系数") 
p.circle(x='index',y='zxjl_pearson',source = source, size = 8,color = 'red',alpha = 0.8,legend="中心距离相关系数")
# 绘制折线图4
p.legend.location = "center_right"
show(p)
# 绘制折线图

 

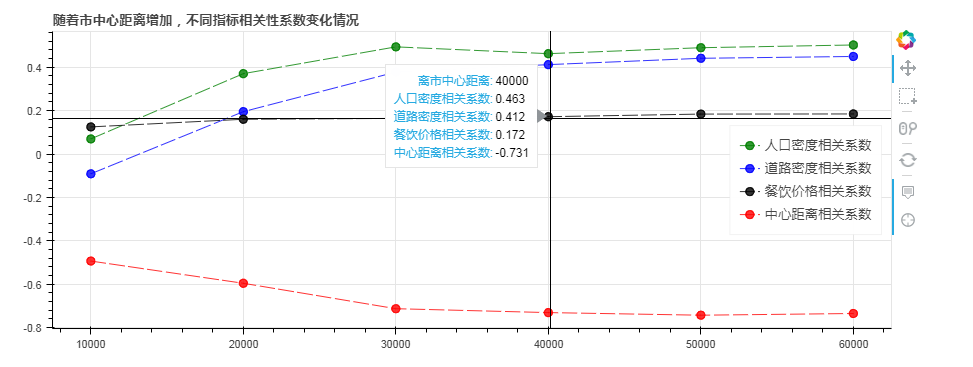
# 结论
# ① “人口密度”、“道路密度”、“离市中心距离”和“房屋均价”有着明显的相关性，而“餐饮价格”和“房屋均价”相关性较弱
# ② 随着离市中心的距离越远，指标的相关性在数据上体现更明显，而这个分界线大概在20-30km处，这正是上海中心城区和郊区的分界
#    → 上海房价市场的“中心城区-郊区”分化特征
# ③ 中心城区的房产市场对指标因素的影响更加敏锐，而郊区则更迟钝 → 越靠近市中心，影响因素越复杂