K最近邻(KNN)算法
1. knn概述
分类是大数据常见的应用场景之一，通过对历史数据规律的统计，将大量数据进行分类然后发现数据之间的关系，这样当有新的数据进来时，计算机就可以利用这个关系自动进行分类了。更进一步讲，
如果这个分类结果在将来才被证实，比如一场比赛的胜负、一次选举的结果，那么在旁观者看来，就是在利用大数据进行预测了。其实，现在火热的机器学习本质上说就是统计学习。
通过一个比较简单的 KNN 分类算法，展示大数据分类算法的特点和应用，以及各种大数据算法都会用到的数据距离计算方法和特征值处理方法。
分类（Classification）指的是从数据中选出已经分好类的训练集，在该训练集上运用数据挖掘分类的技术，建立分类模型，对于没有分类的数据进行分类的分析方法。
（分类其实就是给数据打标签，标签相对于回归来说它是一个离散的值，比如生病了开多少药物的量这个量是连续的值，是否生病、生的什么病这个是离散值）
（逻辑回归最后计算的是一个离散的值，用于分类分析而不是回归分析）
分类问题的应用场景：分类问题是用于将事物打上一个标签，通常结果为离散值。例如判断一副图片上的动物是一只猫还是一只狗，分类通常是建立在分类回归之上。
本文主要讲基本的分类方法 ----- KNN最邻近分类算法
KNN - 最邻近分类算法 ，简称KNN，最简单的机器学习算法之一。
核心逻辑：在距离空间里，如果一个样本的最接近的K个邻居里，绝大多数属于某个类别，则该样本也属于这个类别。
最邻近分类的python实现方法
在距离空间里，如果一个样本的最接近的k个邻居里，绝大多数属于某个类别，则该样本也属于这个类别
电影分类 / 植物分类
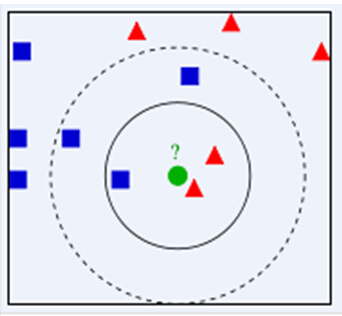
绿色圆(测试数据)要被决定赋予哪个类，是红色三角形还是蓝色四方形？
如果K=3(距离绿色圆最近的3个)，由于红色三角形所占比例为2/3，绿色圆将被赋予红色三角形那个类，
如果K=5(距离绿色圆最近的5个)，由于蓝色四方形比例为3/5，因此绿色圆被赋予蓝色四方形类;
KNN算法的结果很大程度取决于K的选择。
KNN 算法，即 K 近邻（K Nearest Neighbour）算法，是一种基本的分类算法。其主要原理是：对于一个需要分类的数据，将其和一组已经分类标注好的样本集合进行比较，得到距离最近的 K 个样本，K 个样本最多归属的类别，就是这个需要分类数据的类别。
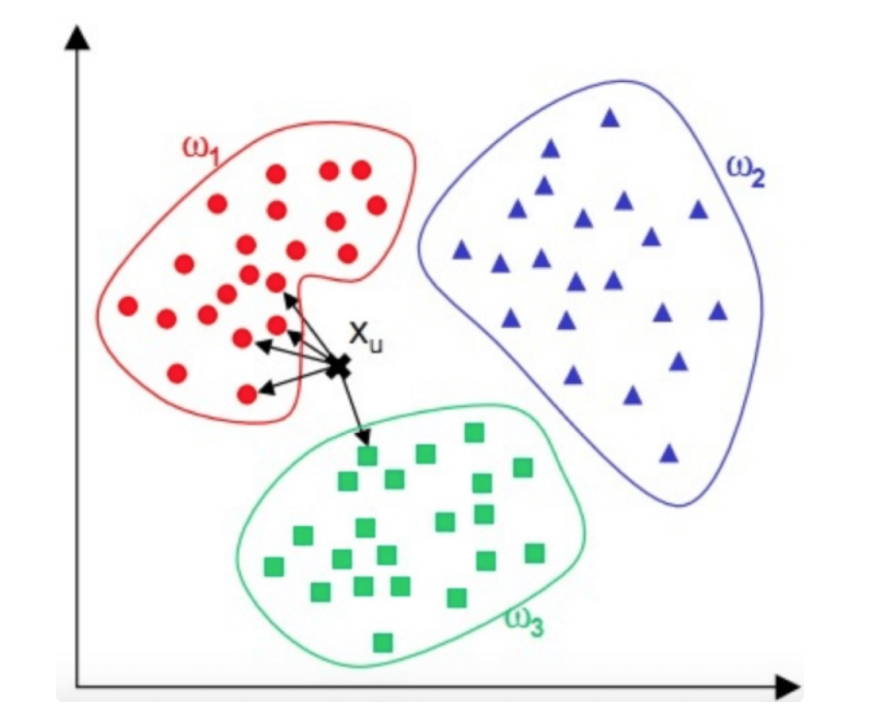
图中，红蓝绿三种颜色的点为样本数据，分属三种类别 w1、w2、 w3 。对于待分类点 Xu ，计算和它距离最近的 5 个点（即 K 为 5），这 5 个点最多归属的类别为 w1（4 个点归属 w1，1 个点归属 w3
），那么 Xu 的类别被分类为 w1。KNN 的算法流程也非常简单，如下流程图：
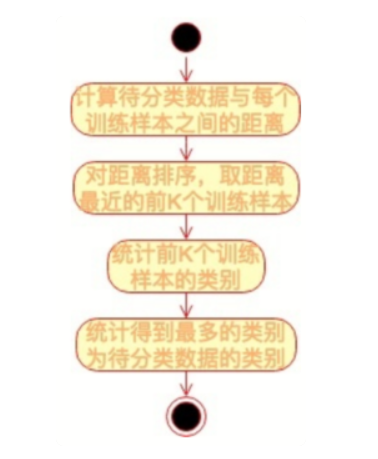
KNN 算法是一种非常简单实用的分类算法，可用于各种分类的场景，比如新闻分类、商品分类等，甚至可用于简单的文字识别。对于新闻分类，可以提前对若干新闻进行人工标注，标好新闻类别，计算
好特征向量。对于一篇未分类的新闻，计算其特征向量后，跟所有已标注新闻进行距离计算，然后进一步利用 KNN 算法进行自动分类。如何计算数据的距离呢？如何获得新闻的特征向量呢？
分类器、回归模型
K-Nearest Neighbors(KNN)
The "hello world" Algorithm
作为分类算法，如何去做
最容易理解的算法，最容易实现的算法；（从0实现不超过5行代码）
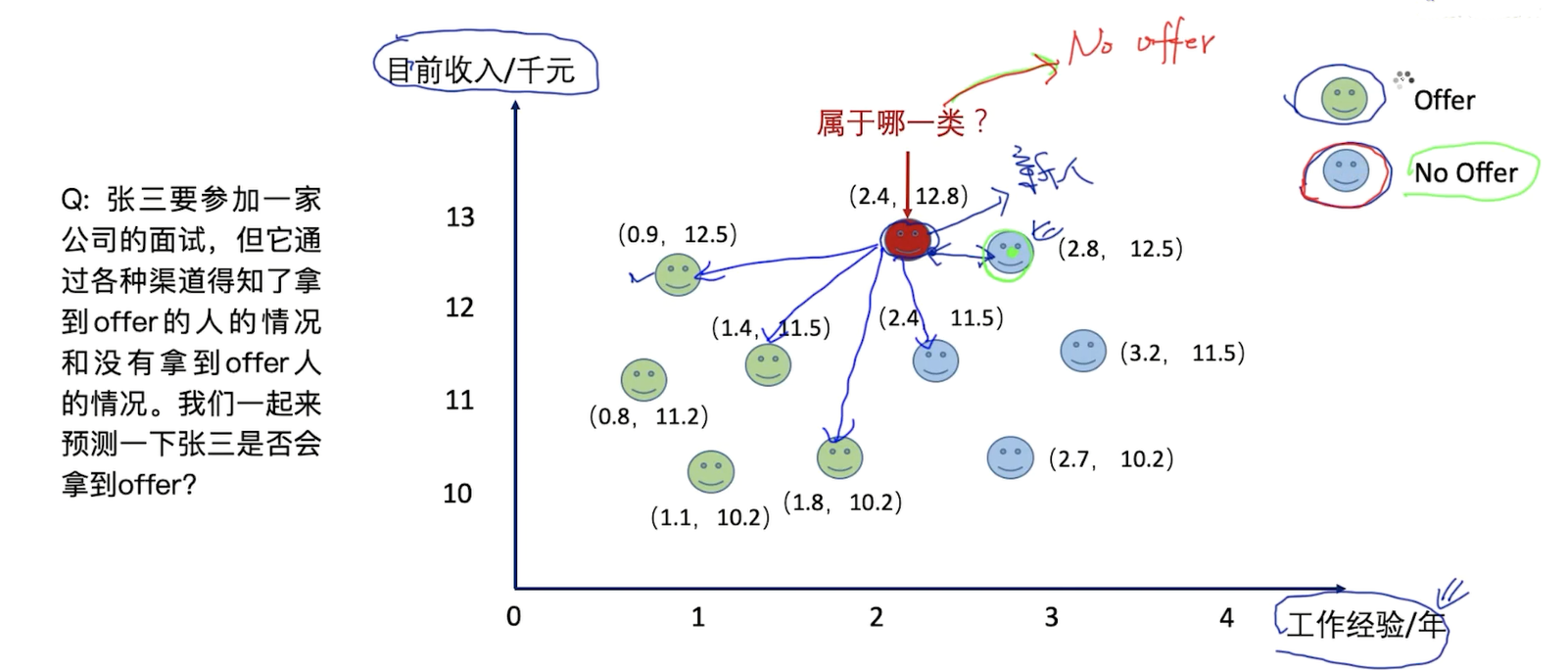
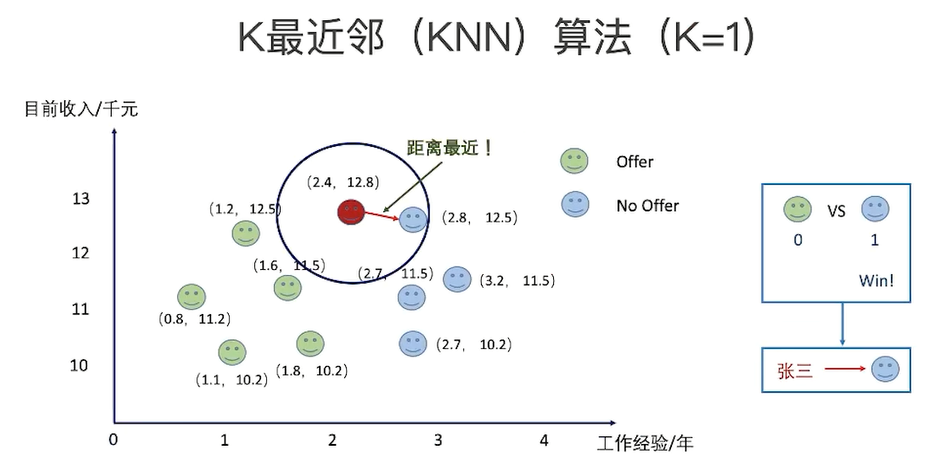
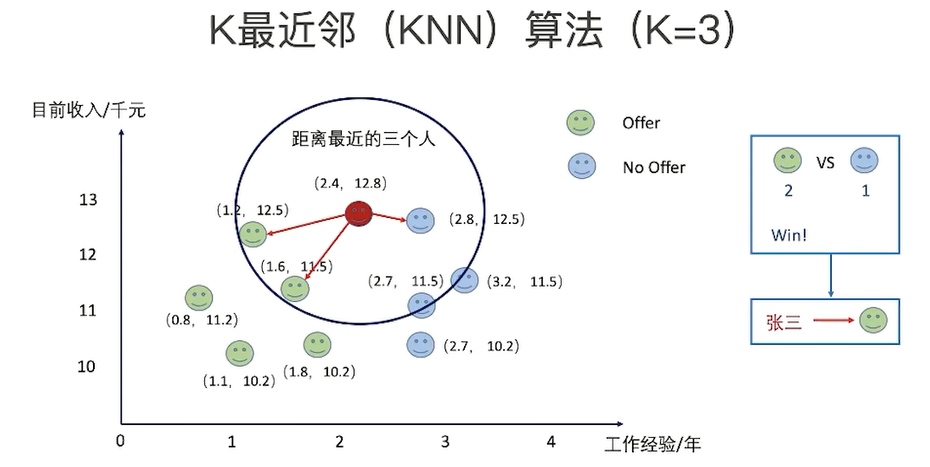
问题： 在使用KNN算法的时候，我们一般会选择奇数（odd-number）的k，为什么？
k = 1, 3, 5, 7, 9...
# 调用KNN函数来实现分类 # 数据采用的是经典的iris数据,是三分类问题 # 读取相应的库 from sklearn import datasets from sklearn.model_selection import train_test_split from sklearn.neighbors import KNeighborsClassifier import numpy as np # 读取数据x, y iris = datasets.load_iris() X = iris.data y = iris.target print(X, y) # 把数据分成训练数据和测试数据 X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=2003) # 构建KNN模型, k值为3, 并做训练 clf = KNeighborsClassifier(n_neighbors=3) clf.fit(X_train, y_train) #训练的过程 # 计算准确率 from sklearn.metrics import accuracy_score correct = np.count_nonzero((clf.predict(X_test) == y_test) == True) #accuracy_score(y_test, clf.predict(X_test)) print("Accuracy is: %.3f" %(correct/len(X_test)))
2. 欧式距离和knn的实现
KNN 算法的关键是要比较需要分类的数据与样本数据之间的距离，这在机器学习中通常的做法是：提取数据的特征值，根据特征值组成一个 n 维实数向量空间（这个空间也被称作特征空间），然后计算
向量之间的空间距离。空间之间的距离计算方法有很多种，常用的有欧氏距离、余弦距离等。
对于数据 xi 和 xj，若其特征空间为 n 维实数向量空间 Rn，即 xi=(xi1,xi2,…,xin)，xj=(xj1,xj2,…,xjn)，则其欧氏距离计算公式为
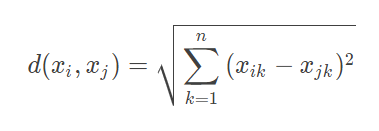
平面几何和立体几何里两个点之间的距离，也是用这个公式计算出来的，只是平面几何（二维几何）里的n=2，立体几何（三维几何）里的 n=3，而机器学习需要面对的每个数据都可能有 n 维的维度，即
每个数据有 n 个特征值。但是不管特征值 n 是多少，两个数据之间的空间距离的计算公式还是这个欧氏计算公式。大多数机器学习算法都需要计算数据之间的距离，因此掌握数据的距离计算公式是掌握
机器学习算法的基础。欧氏距离是最常用的数据计算公式，但是在文本数据以及用户评价数据的机器学习中，更常用的距离计算方法是余弦相似度。
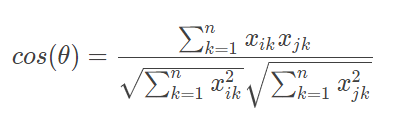
余弦相似度的值越接近 1 表示其越相似，越接近 0 表示其差异越大，使用余弦相似度可以消除数据的某些冗余信息，某些情况下更贴近数据的本质。比如两篇文章的特征值都是：“大数据”“机器学习”和“极
客时间”，A 文章的特征向量为（3, 3, 3），即这三个词出现次数都是 3；B 文章的特征向量为（6, 6, 6），即这三个词出现次数都是 6。如果光看特征向量，这两个向量差别很大，如果用欧氏距离计算确
实也很大，但是这两篇文章其实非常相似，只是篇幅不同而已，它们的余弦相似度为 1，表示非常相似。余弦相似度其实是计算向量的夹角，而欧氏距离公式是计算空间距离。余弦相似度更关注数据的相
似性，比如两个用户给两件商品的打分分别是（3, 3）和（4, 4），那么两个用户对两件商品的喜好是相似的，这种情况下，余弦相似度比欧氏距离更合理。
文本的特征值
知道了机器学习的算法需要计算距离，而计算距离还需要知道数据的特征向量，因此提取数据的特征向量是机器学习工程师们的重要工作。不同的数据以及不同的应用场景，需要提取不同的特征值，以
比较常见的文本数据为例，看看如何提取文本特征向量。
文本数据的特征值就是提取文本关键词，TF-IDF 算法是比较常用且直观的一种文本关键词提取算法。这种算法是由 TF 和 IDF 两部分构成。
TF 是词频（Term Frequency），表示某个单词在文档中出现的频率，一个单词在一个文档中出现得越频繁，TF 值越高。
词频：
IDF 是逆文档频率（Inverse Document Frequency），表示这个单词在所有文档中的稀缺程度，越少文档出现这个词，IDF 值越高。
逆文档频率：
TF 与 IDF 的乘积就是 TF-IDF。TF−IDF=TF×IDF。
所以如果一个词在某一个文档中频繁出现，但在所有文档中却很少出现，那么这个词很可能就是这个文档的关键词。比如一篇关于原子能的技术文章，“核裂变”“放射性”“半衰期”等词汇会在这篇文档中频
繁出现，即 TF 很高；但是在所有文档中出现的频率却比较低，即 IDF 也比较高。因此这几个词的 TF-IDF 值就会很高，就可能是这篇文档的关键词。如果这是一篇关于中国原子能的文章，也许“中国”这
个词也会频繁出现，即 TF 也很高，但是“中国”也在很多文档中出现，那么 IDF 就会比较低，最后“中国”这个词的 TF-IDF 就很低，不会成为这个文档的关键词。提取出关键词以后，就可以利用关键词的
词频构造特征向量，比如上面例子关于原子能的文章，“核裂变”“放射性”“半衰期”这三个词是特征值，分别出现次数为 12、9、4。那么这篇文章的特征向量就是（12, 9, 4），再利用前面提到的空间距离计
算公式计算与其他文档的距离，结合 KNN 算法就可以实现文档的自动分类。
KNN中，通过计算对象间距离来作为各个对象之间的非相似性指标，避免了对象之间的匹配问题，在这里距离一般使用欧氏距离或曼哈顿距离：
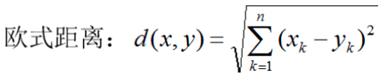
（一般选择曼哈顿距离）
KNN算法
在训练集中数据和标签已知的情况下，输入测试数据，将测试数据的特征与训练集中对应的特征进行相互比较，找到训练集中与之最为相似的前K个数据，则该测试数据对应的类别就是K个数据中出现次数最多的那个分类，其算法的描述为：
- 计算测试数据与各个训练数据之间的距离；
- 按照距离的递增关系进行排序；
- 选取距离最小的K个点；
- 确定前K个点所在类别的出现频率；
- 返回前K个点中出现频率最高的类别作为测试数据的预测分类
有几个需要考虑的问题
① 把一个物体表示成向量
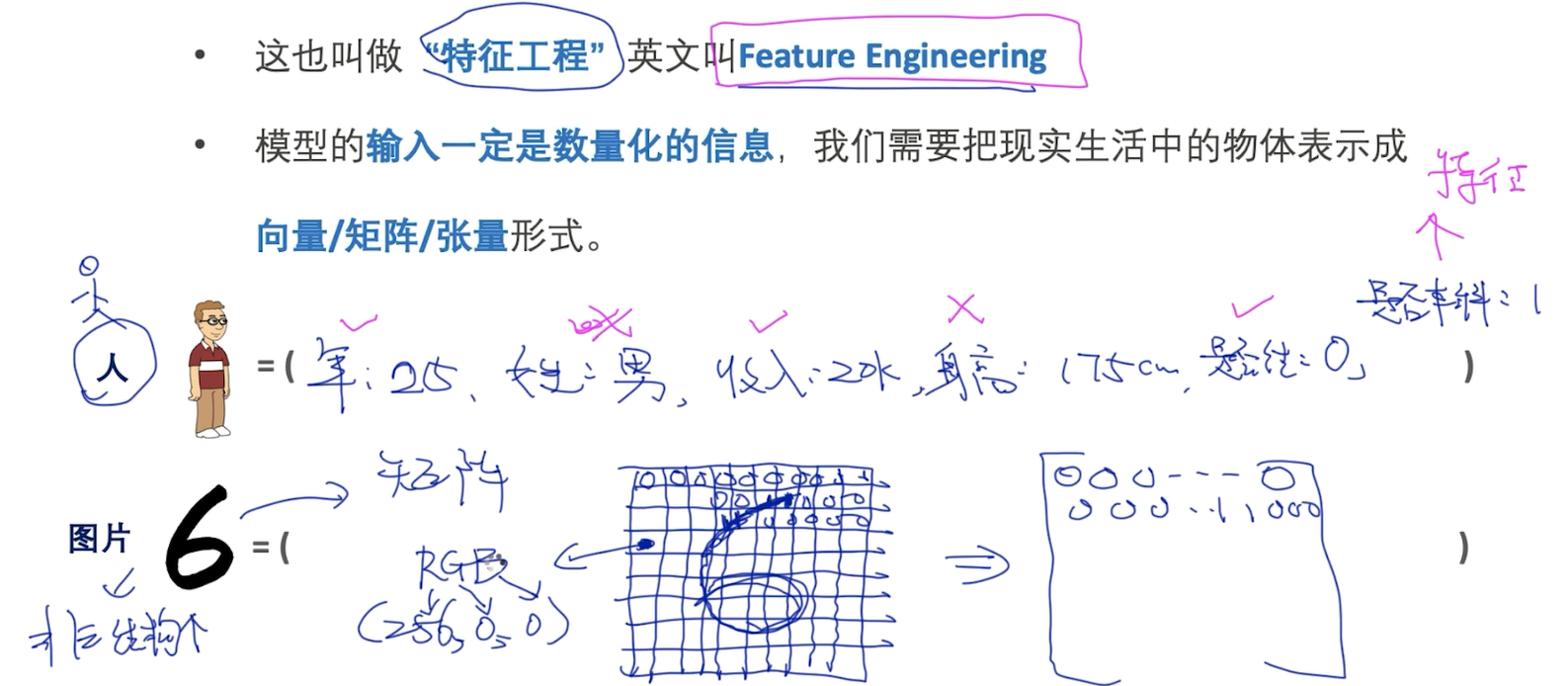
② 标记好每个物体的标签
③ 计算两个物体之间的距离/ 相似度
三维特征 x = (x1, x2, x3)
y = (y1, y2, y3)
欧式距离： dE (x, y)= ((x1- y1)2 + (x2 - y2)2 + (x3 - y3)2 ) 1/2
# 从零开始自己手动实现KNN算法 from sklearn import datasets from collections import Counter #为了做投票 from sklearn.model_selection import train_test_split import numpy as np #导入 iris数据 iris = datasets.load_iris() X = iris.data y = iris.target X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=2003) def euc_dis(instance1, instance2): ''' 计算两个样本instance1和 instance2之间的欧式距离 instance1: 第一个样本,array型 instance2: 第二个样本,array型 :param instance1: :param instance2: :return: ''' # TODO dist = np.sqrt(sum((instance1 - instance2) ** 2)) return dist def knn_classify(X, y, testInstance, k): ''' 给定一个测试数据testInstance, 通过KNN算法来预测它的标签; X: 训练数据的特征 y: 训练数据的标签 testInstance: 测试数据,这里假定一个测试数据 array型 k: 选择多少个neighbors? :param X: :param y: :param testInstance: :param k: :return: ''' # TODO 返回testInstance的预测标签 = {0, 1, 2} # 时间复杂度: O(N) N是number of samples distances = [euc_dis(x, testInstance) for x in X] # argsort 排序它的时间复杂度是 O(NlogN) 优化 使用priority queue -> O(NlogK) kneighbors = np.argsort(distances)[:k] count = Counter(y[kneighbors]) print(count) return count.most_common()[0][0] #预测结果 predictions = [knn_classify(X_train, y_train, data, 3) for data in X_test] correct = np.count_nonzero((predictions == y_test) == True) #accuracy_score(y_test, clf.predict(X_test)) print("Accuracy is: %.3f" %(correct/len(X_test)))
3. 选择合适的k
为了选择合理的k，首先需要去理解k对算法的影响；
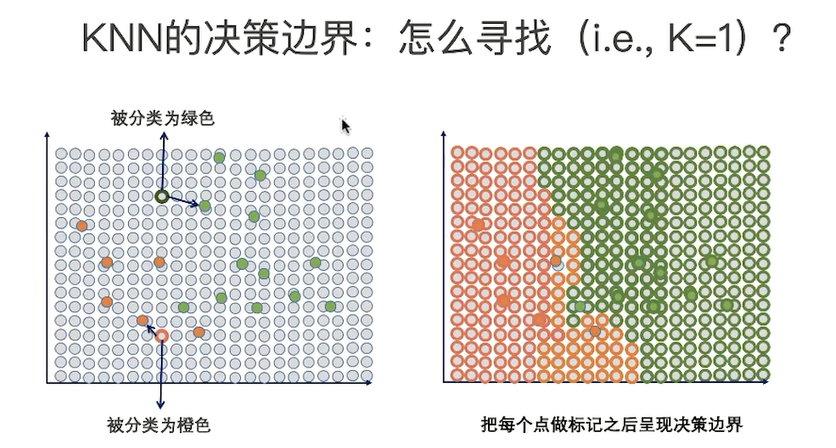
为了理解k对算法的影响，需要小理解什么叫算法的决策边界；
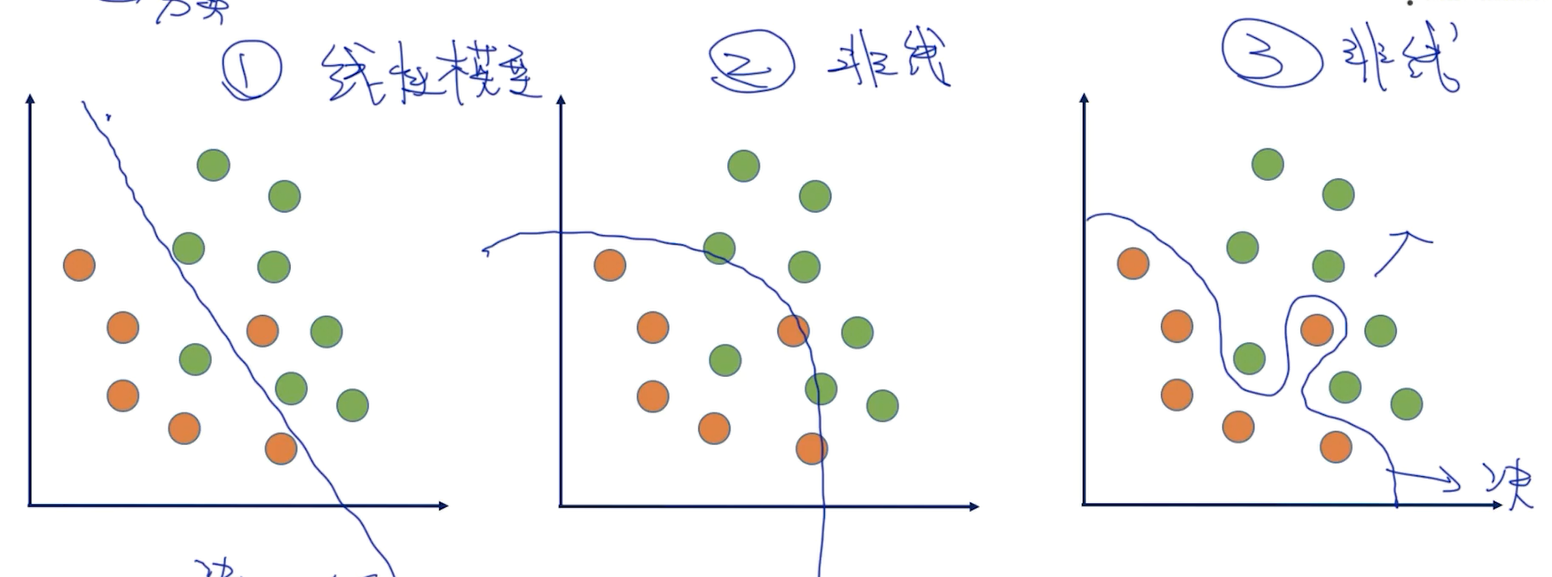
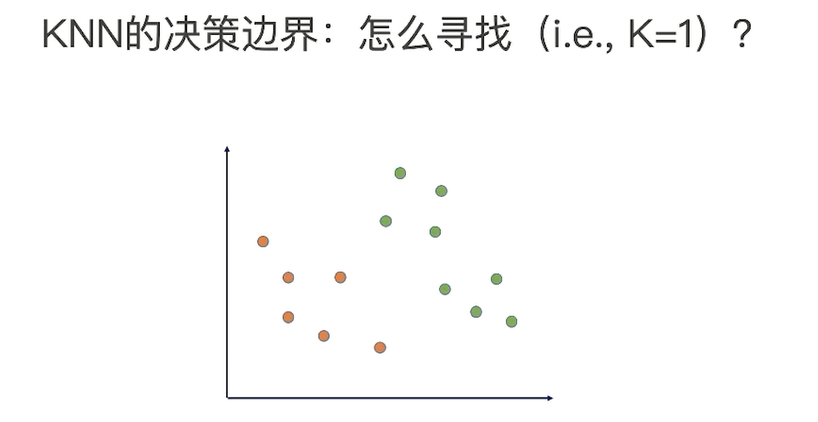
二分类问题，学出决策边界，三种不同的决策边界：
哪个决策边界是最好的？
准确率和稳定性
import matplotlib.pyplot as plt import numpy as np from itertools import product from sklearn.neighbors import KNeighborsClassifier # 生成一些随机样本 n_points = 100 X1 = np.random.multivariate_normal([1, 50], [[1, 0], [0,10]], n_points) X2 = np.random.multivariate_normal([2, 50], [[1, 0], [0, 10]], n_points) X = np.concatenate([X1, X2]) y = np.array([0]*n_points + [1]*n_points) print(X.shape, y.shape) # KNN模型的训练过程 clfs = [] neighbors = [1,3,5,9,11,13,15,17,19] for i in range(len(neighbors)): clfs.append(KNeighborsClassifier(n_neighbors=neighbors[i]).fit(X, y)) #可视化结果 x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1 y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1 XX, yy = np.meshgrid(np.arange(x_min, x_max, 0.1), np.arange(y_min, y_max, 0.1)) f, axarr = plt.subplots(3, 3, sharex='col', sharey='row', figsize=(15, 12)) for idx, clf, tt in zip(product([0, 1, 2], [0, 1, 2]), clfs, ['KNN (K=%d)' %k for k in neighbors]): Z = clf.predict(np.c_[XX.ravel(), yy.ravel()]) Z = Z.reshape(XX.shape) axarr[idx[0], idx[1]].contourf(XX, yy, Z, alpha=0.4) axarr[idx[0], idx[1]].scatter(X[:, 0], X[:, 1], c=y, s=20, edgecolor='k') axarr[idx[0], idx[1]].set_title(tt) plt.show()
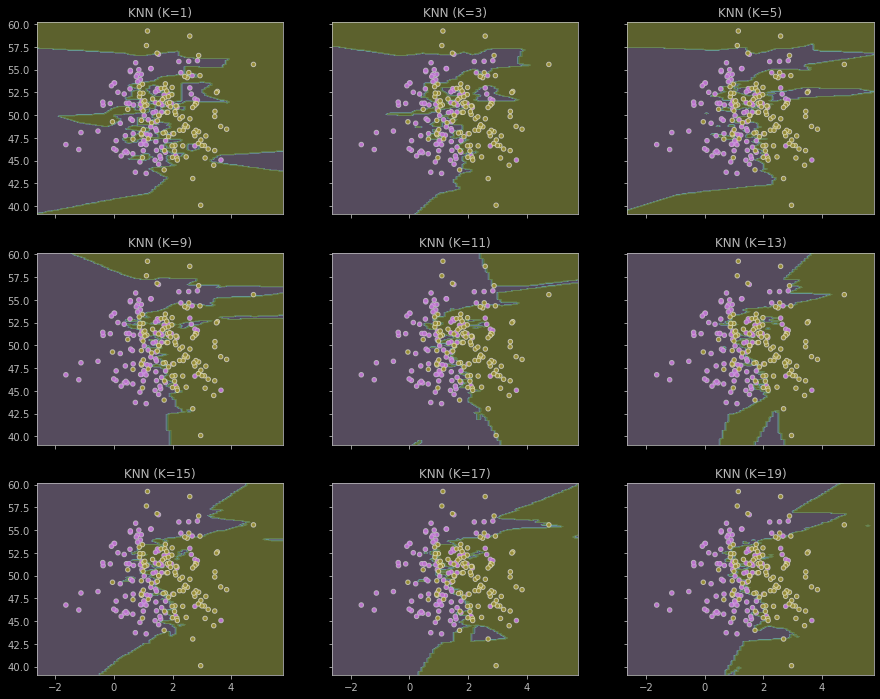
4. 通过交叉验证选择K
KNN的决策边界，K值的影响
问题：随着K的增加，会怎么变化
怎么去选择合适的K
交叉验证
5折交叉验证（5-fold Cross Validation）
通过训练数据，在验证数据中去验证，得到一个acc1，以此类推得到acc2、acc3、acc4、acc5等，最后得到平均准确率 acc平均|k=1 = (acc1 + acc2 +...+ acc5) / 5
k=3也是类似的；
交叉验证中需要注意的点
- 千万不能用测试数据来调参；
- 数据量越少，可以适当增加折数；
KNN需要考虑的点
第一个特征起不到作用，因为第二个特征占据了绝对主导的作用；它俩的范围差距太大；
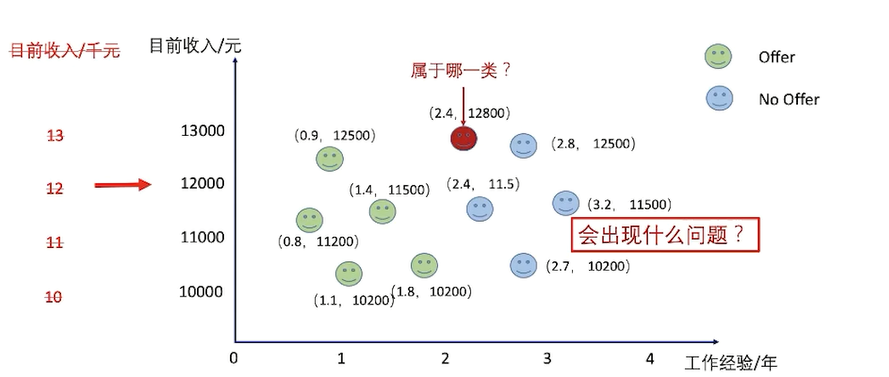
特征的缩放
特征缩放 - 线性归一化（Min-max Normalization）
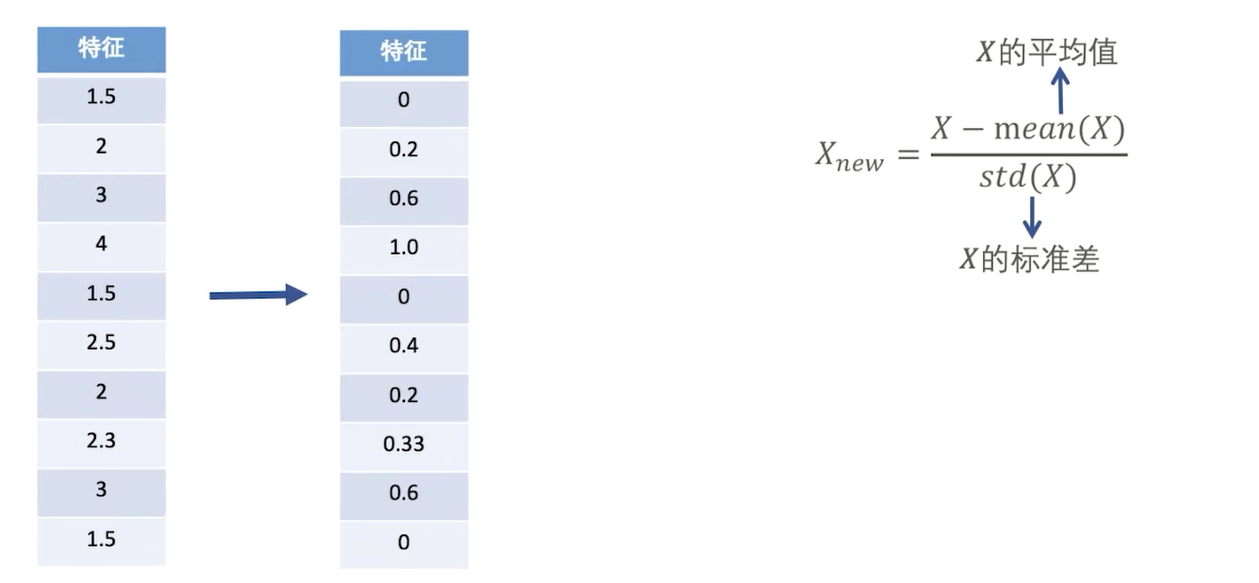
特征缩放 - 标准差标准化（Z-score-Normalization）
延伸内容
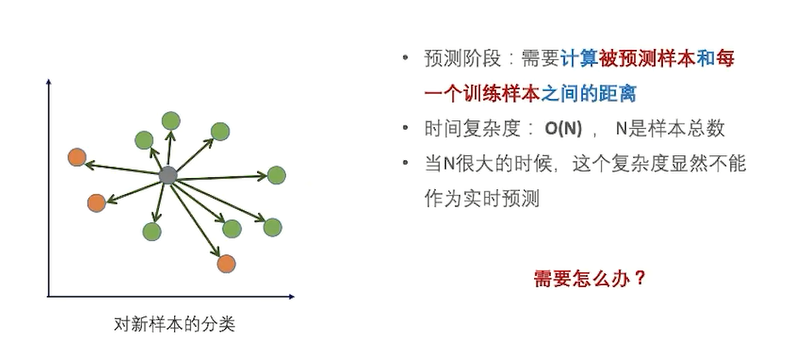
如何处理大数据量
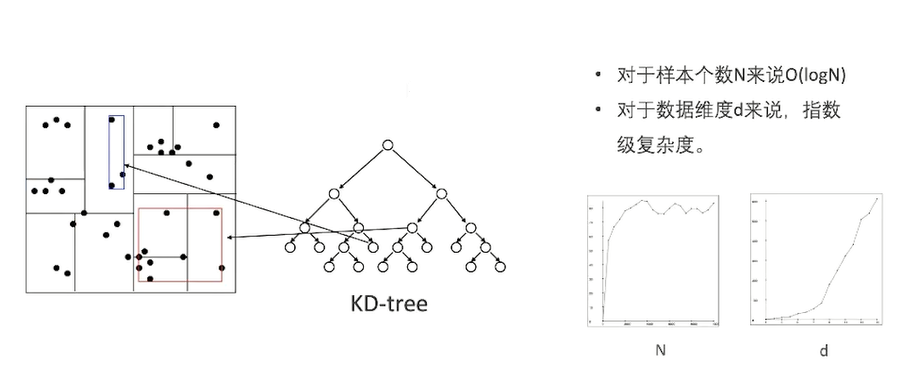
KD- tree
LSH哈希算法 - 解决高纬度问题
欧氏距离，假设这三个都是独立的
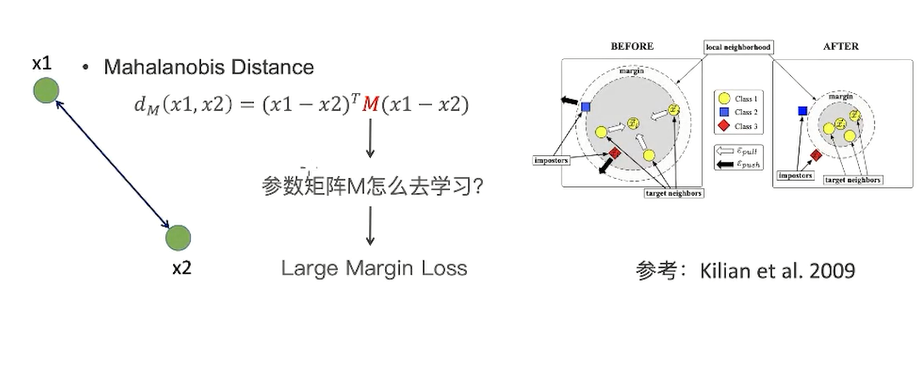
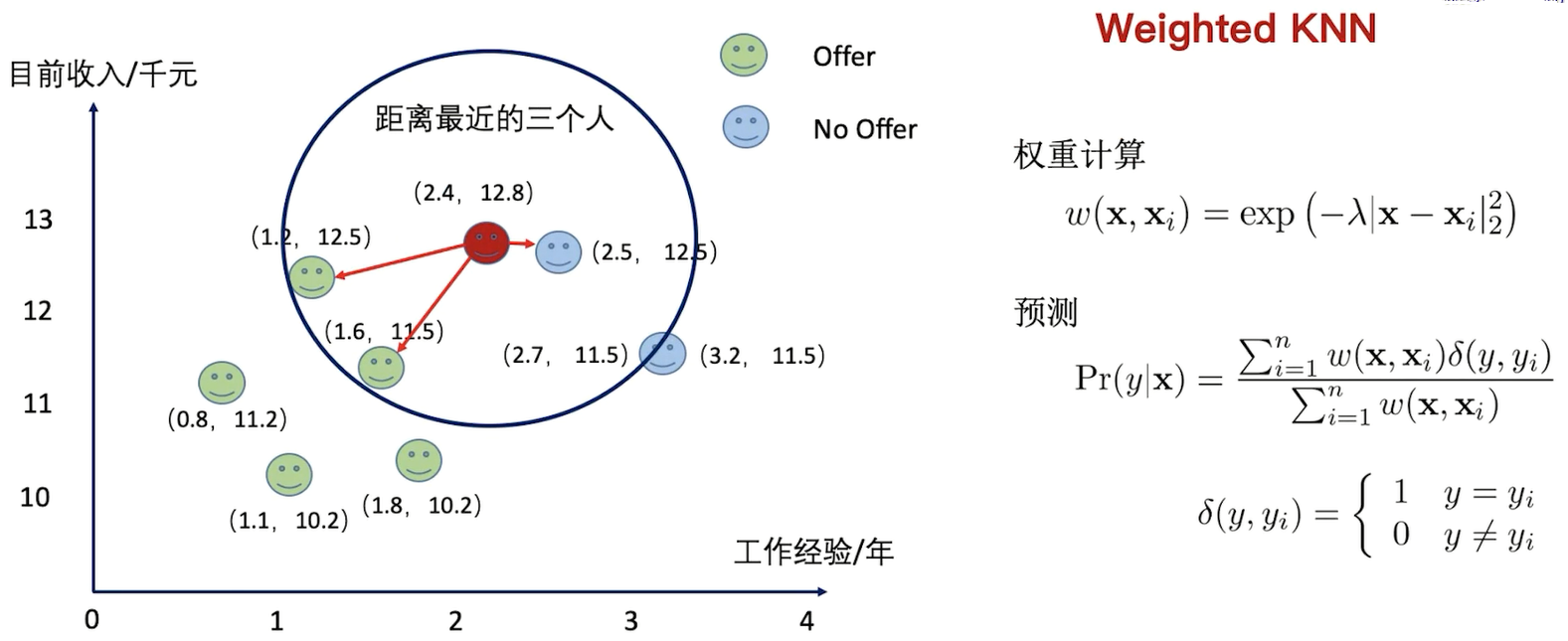
利用权重的方式构建KNN，距离越小，权重越大
Kernel Trick
总结：
- KNN是一个非常简单的算法；
- 比较适合应用在低维空间；
- 预测时候的复杂度高，对于大数据需要一定的处理；
