01. Numpy模块
1. 科学计算工具-Numpy基础数据结构
Numpy - Python开源的科学计算工具包
NumPy 中文, Numpy(Numerical Python)是一个开源的Python科学计算库,用于快速处理任意维度的数组。支持常见的数组和矩阵操作,对于同样的数值计算任务,
Numpy使用ndarray对象来处理多维数组,该对象是一个快速而灵活的大数据容器。(快速、方便、科学计算库)
Numpy的优势
- 对于同样的数值计算任务,numpy要比直接编写python代码便捷的多;
- numpy中的数组存储效率和输入输出性能均远远优于python中等价的基本数据结构,且能够提升的性能是与数组中的元素成比例的;
- Numpy大部分代码用C语言写的,其底层算法在设计时就有着优异的性能。
#Numpy 与原生List的对比
import numpy as np
import time
import random
a = []
for i in range(1000000000):
a.append(random.random())
t1 = time.time()
sum1 = sum(a)
t2 = time.time()
b = np.array(a)
t3 = time.time()
sum2 = np.sum(b)
t4 = time.time()
print(t2 - t1, t4 - t3)
0.4079601764678955 0.10870957374572754
t2 - t1使用python自带的求和和 函数消耗的时间;
t4 - t3使用numpy求和消耗的时间,从中可以看到ndarray的计算速度要快的多,节约了时间。
- 高级的数值编程工具
- 强大的N维数组对象:ndarray
- 对数组结构数据进行运算(不用遍历循环)
- 随机数、线性代数、博里叶变换等功能
- 许多高级工具的构建基础,比如Pandas
1.1 数组ndarray的基本属性
Numpy最重要的一个特点是其N维数组对象ndarray,它是一系列同类型数据的集合,以0下标为开始进行集合中元素的索引。ndarray对象是用于存放同类型元素的多维数组。
NumPy数组是一个多维数组对象,称为ndarray。其由两部分组成:
① 实际的数据
② 描述这些数据的元数据
注意数组格式,中括号,元素之间没有逗号(和列表的区别)
① 数组的维数称为秩(rank),一维数组的秩为1,二维数组的秩为2,以此类推
② 在NumPy中,每一个线性的数组称为是一个轴(axes),秩其实是描述轴的数量:
比如说,二维数组相当于是两个一维数组,其中第一个一维数组中每个元素又是一个一维数组,所以一维数组就是NumPy中的轴(axes),第一个轴相当于是底层数组,第二个轴是底层数组里的数组。
而轴的数量——秩,就是数组的维数。
ndarray的数据类型
- bool 用一个字节存储的布尔类型(True或False)
- inti 由所在平台决定其大小的整数(一般为int32或int64)
- int8 一个字节大小,-128 至 127
- int16 整数,-32768 至 32767
- int32 整数,-2 31 至 2 32 -1
- int64 整数,-2 63 至 2 63 - 1
- uint8 无符号整数,0 至 255
- uint16 无符号整数,0 至 65535
- uint32 无符号整数,0 至 2 ** 32 - 1
- uint64 无符号整数,0 至 2 ** 64 - 1
- float16 半精度浮点数:16位,正负号1位,指数5位,精度10位
- float32 单精度浮点数:32位,正负号1位,指数8位,精度23位
- float64或float 双精度浮点数:64位,正负号1位,指数11位,精度52位
- complex64 复数,分别用两个32位浮点数表示实部和虚部
- complex128或complex 复数,分别用两个64位浮点数表示实部和虚部
import numpy as np
ar = np.array([[1,2,3,4,5,6], [2,3,4,5,6,7], [3,4,5,6,7,8]]) #3行6列的二维数组
#ar = np.array([[[1,2,3,4,5,6], [2,3,4,5,6,7], [3,4,5,6,7,8]], [[1,2,3,4,5,6], [2,3,4,5,6,7], [3,4,5,6,7,8]]]) #2个二维数组或多个二维数组即三维数组
print(ar, type(ar), ar.dtype) #type()是查看变量的类型(type()是函数,.dtype是方法查看数值的类型)
print(ar.ndim) #输出数组维度的个数(轴数),或者说“秩”,维度的数量也称rank,即几维数组
print(ar.shape) ## 数组的维度,对于n行m列的数组,shape为(n,m)
print(ar.size) # 数组的元素总数,对于n行m列的数组,元素总数为n*m
print(ar.itemsize) # 数组中每个元素的字节大小,int32类型字节为4,float64的字节为8
print(ar.data) # 包含实际数组元素的缓冲区,由于一般通过数组的索引获取元素,所以通常不需要使用这个属性。
ar # 交互方式下输出,会有array(数组)
打印:
[[1 2 3 4 5 6]
[2 3 4 5 6 7]
[3 4 5 6 7 8]] <class 'numpy.ndarray'> int32
2
(3, 6)
18
4
array([[1, 2, 3, 4, 5, 6],
[2, 3, 4, 5, 6, 7],
[3, 4, 5, 6, 7, 8]])
1.2 数组的创建
创建数组方法一:array(), arange()函数
np.array(列表、元组、数组、生成器 ) 如:np.array(range(10)) ,如果有两个嵌套序列,长度不一样就会变成一维数组;
np.arange(5, 12, 2)返回5-11的数步长为2 ,类似range(),在给定间隔内返回均匀间隔的值
>>> ar1 = np.array(range(10)) #整型 >>> print(ar1) [0 1 2 3 4 5 6 7 8 9]
>>> ar2 = np.arange(10) >>> print(ar2) [0 1 2 3 4 5 6 7 8 9]
>>> ar4 = np.array([[1,2,3,4,5],[5,6,7,8,9,10]]) #嵌套序列不一样就会变成一维数组 >>> print(ar4,type(ar4),ar4.dtype,ar4.ndim) [list([1, 2, 3, 4, 5]) list([5, 6, 7, 8, 9, 10])] <class 'numpy.ndarray'> object 1
>>> ar4 = np.array([[1,2,3],('a','b','c')]) ######二维数组,嵌套序列,可以是列表可以是元组。 >>> print(ar4, ar4.shape, ar4.ndim, ar4.size) [['1' '2' '3'] ['a' 'b' 'c']] (2, 3) 2 6 >>> print(np.random.rand(10).reshape(2,5)) ###随机数组,10个0-1的数字,2乘以5 [[0.927168 0.77335508 0.0120362 0.1504996 0.93548895] [0.34811207 0.41284246 0.75599419 0.53838818 0.74908313]]
创建数组方法二:linspace( )
numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None) 如np.linspace(10, 20, 11) ,返回在间隔[开始,停止]上计算的num个均匀间隔的样本。
- start:起始值,stop:结束值
- num:生成样本数,默认为50
- endpoint:默认值为True(可不写),即包含最后一个值。endpoint = False 是不包含最后一个值。
- retstep:默认值为False(可不写),即步长不显示出来;如果为真retstep = True就会返回样本的步长(间距)。返回(样本,步骤),其中步长是样本之间的间距 → 输出为一个包含2个元素的元祖,第一个元素为array,第二个为步长实际值
>>> print(np.linspace(10,20,num=21)) #10-20,前后都是闭合,都可以取到; 默认endpoint = True包含最后一个值 [10. 10.5 11. 11.5 12. 12.5 13. 13.5 14. 14.5 15. 15.5 16. 16.5 17. 17.5 18. 18.5 19. 19.5 20. ]
>>> print(np.linspace(10,20,num=21,endpoint = False)) #默认是True, False是最后一个值不包含; [10. 10.47619048 10.95238095 11.42857143 11.9047619 12.38095238 12.85714286 13.33333333 13.80952381 14.28571429 14.76190476 15.23809524 15.71428571 16.19047619 16.66666667 17.14285714 17.61904762 18.0952381 18.57142857 19.04761905 19.52380952]
>>> s = np.linspace(10,20,num=21,retstep = True) #返回样本的步长 ,默认restep = False >>> print(s, type(s)) (array([10. , 10.5, 11. , 11.5, 12. , 12.5, 13. , 13.5, 14. , 14.5, 15. , 15.5, 16. , 16.5, 17. , 17.5, 18. , 18.5, 19. , 19.5, 20. ]), 0.5) <class 'tuple'> #2个元素,一个为array,另一个为步长。 >>> print(s[0]) [10. 10.5 11. 11.5 12. 12.5 13. 13.5 14. 14.5 15. 15.5 16. 16.5 17. 17.5 18. 18.5 19. 19.5 20. ]
创建数组方法三:zeros( ), zeros_like( )/ ones( ), ones_like( )
np.zeros((3, 5), dtype=np.int )、np.zeros_like(ar)
# numpy.zeros(shape, dtype=float, order='C'):返回给定形状和类型的新数组,用零填充。
shape:数组纬度,二维以上需要用(),且输入参数为整数
dtype:数据类型,默认numpy.float64
order:是否在存储器中以C或Fortran连续(按行或列方式)存储多维数据。
>>> print(np.zeros(5))
[0. 0. 0. 0. 0.]
>>> print(np.zeros((3,5)))
[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]
>>> print(np.zeros((3,5), dtype=np.int))
[[0 0 0 0 0]
[0 0 0 0 0]
[0 0 0 0 0]]
>>> ar = np.array([list(range(10)),list(range(10,20))])
>>> print(ar)
[[ 0 1 2 3 4 5 6 7 8 9]
[10 11 12 13 14 15 16 17 18 19]]
>>> print(np.zeros_like(ar))
[[0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0]]
>>> ar2 = np.ones(9)
>>> ar3 = np.ones((2,3,4))
>>> ar4 = np.ones_like(ar3)
>>> print(ar2)
[1. 1. 1. 1. 1. 1. 1. 1. 1.]
>>> print(ar3)
[[[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]
[[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]]
>>> print(ar4)
[[[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]
[[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]]
创建数组方法四:eye( )
# 创建一个正方的N * N 的单位矩阵,对角线值为1,其余为0
>>> print(np.eye(5))
[[1. 0. 0. 0. 0.]
[0. 1. 0. 0. 0.]
[0. 0. 1. 0. 0.]
[0. 0. 0. 1. 0.]
[0. 0. 0. 0. 1.]]
2. Numpy通用函数
2.1 数组形状
① ar.T(一维数组转置后结果不变,二维数组如shape(2,5), .T转置后为shape(5,2))
② ar.reshape(2,5) 直接将已有数组改变形状;np.zero((2,3)).reshape(3,2)生成数组后直接改变形状;np.reshape(np.arange(12),(3,4))参数内添加数组,目标形状
numpy.reshape(a, newshape, order='C'):为数组提供新形状,而不更改其数据,所以元素数量需要一致!!
③ np.resize(np.arange(5), (3,4))
numpy.resize(a, new_shape):返回具有指定形状的新数组,如有必要可重复填充所需数量的元素。
注意了:.T/ .reshape( )/ .resize( )都是生成新的数组!!!
④ 将多维数组转换为一维 arr.reshape((6,), order = 'F')
>>> import numpy as np >>> ar1 = np.arange(10)
>>> print(ar1, '\n', ar1.T) #一维数组转置后结果不变 [0 1 2 3 4 5 6 7 8 9] [0 1 2 3 4 5 6 7 8 9]
>>> ar2 = np.ones((5,2)) >>> print(ar2, '\n', ar2.T) [[1. 1.] [1. 1.] [1. 1.] [1. 1.] [1. 1.]] [[1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.]]
# .T方法:转置,例如原shape为(3,4)/(2,3,4),转置结果为(4,3)/(4,3,2) → 所以一维数组转置后结果不变 >>> ar3 = ar1.reshape(2,5) #reshape用法一,直接将已有数组改变形状。 >>> print(ar1,'\n',ar3) [0 1 2 3 4 5 6 7 8 9] [[0 1 2 3 4] [5 6 7 8 9]]
>>> ar4 = np.zeros((4,6)).reshape(3,8) #reshape用法二,生成数组后直接改变形状。 >>> print(ar4) [[0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0.]]
>>> ar5 = np.reshape(np.arange(12),(3,4)) #reshape用法三,参数内添加数组,目标形状。 >>> print(ar5) [[ 0 1 2 3] [ 4 5 6 7] [ 8 9 10 11]]
>>> ar6 = np.resize(np.arange(5),(3,4)) >>> print(ar6) [[0 1 2 3] [4 0 1 2] [3 4 0 1]]
arr2 = np.array([[1,2,3], [4,5,6]])
# 将多维变成一维数组 默认情况下'C'以行为主的顺序展开, 'F'(Fortran风格)以列的顺序展开
print(arr2.reshape((6,), order='F'))
# [1 4 2 5 3 6]
print(arr2.reshape((6,))) # 可省略, order='C'
# [1 2 3 4 5 6]
print(arr2.tolist()) #将数组转换为list
#[[1, 2, 3], [4, 5, 6]]
2.2 数组的复制(赋值=, copy( ))
赋值进行修改ar1中的值,ar2也会改变,它们指向的是同一个数值。
而使用copy方法( ar1.copy( ) )再去进行修改,就不会变了。
>>> ar1 = np.arange(10) >>> ar2 = ar1 >>> print(ar2 is ar1) True >>> ar1[2] = 9 #赋值,ar1改变,ar2也会改变; >>> print(ar1, ar2) [0 1 9 3 4 5 6 7 8 9] [0 1 9 3 4 5 6 7 8 9]
# 回忆python的赋值逻辑:指向内存中生成的一个值 → 这里ar1和ar2指向同一个值,所以ar1改变,ar2一起改变
>>> ar3 = ar1.copy() >>> print(ar3 is ar1) False >>> ar1[0] = 9 >>> print(ar1, ar3) #copy()方法,ar1改变,ar3不会变 [9 1 9 3 4 5 6 7 8 9] [0 1 9 3 4 5 6 7 8 9]
# copy方法生成数组及其数据的完整拷贝
2.3 数组类型转换:.astype( )
ar1.astype(np.int64)
>>> ar1 = np.arange(10, dtype=float)
>>> print(ar1, ar1.dtype)
[0. 1. 2. 3. 4. 5. 6. 7. 8. 9.] float64
# 可以在参数位置设置数组类型
>>> ar2 = ar1.astype(np.int32)
>>> print(ar2, ar2.dtype)
[0 1 2 3 4 5 6 7 8 9] int32
# a.astype():转换数组类型
# 注意:养成好习惯,数组类型用np.int32,而不是直接int32
2.4 数组堆叠
np.hstack((数组1,数组2) ) 水平堆叠数组,括号内的如果是一维数组形状可以不一样,二维数组形状要一致 (水平堆叠,堆这堆这缺位了不行呀)
np.vstack((a,b))垂直堆叠数组,
np.stack((a,b),axis = 1) axis默认为0,可不写,即按照垂直的堆,注意跟vstack的区别; axis=1即按照横向的堆与hstack不一样的哦。
>>> a = np.arange(5) #a为一维数组,5个元素;
>>> b = np.arange(5,9) #b为一维数组,4个元素;
>>> ar1 = np.hstack((a,b)) #注意:一维数组((a,b))这里形状可以不一样。
>>> print(a, a.shape)
[0 1 2 3 4] (5,)
>>> print(b, b.shape)
[5 6 7 8] (4,)
>>> print(ar1, ar1.shape)
[0 1 2 3 4 5 6 7 8] (9,)
>>> a = np.array([[1],[2],[3]]) #a为二维数组,3行1列;
>>> b = np.array([['a'],['b'],['c']]) #b为二维数组,3行1列;
>>> ar2 = np.hstack((a,b)) #((a,b)),这里a,b形状必须一致。水平(按列顺序)堆叠数组
>>> print(a,a.shape,'\n', b,b.shape)
[[1]
[2]
[3]] (3, 1)
[['a']
['b']
['c']] (3, 1)
>>> print(ar2,ar2.shape)
[['1' 'a']
['2' 'b']
['3' 'c']] (3, 2)
# numpy.hstack(tup):水平(按列顺序)堆叠数组
>>> a = np.arange(5)
>>> b = np.arange(5,10)
>>> ar1 = np.vstack((a,b))
>>> print(a,a.shape,'\n', b,b.shape)
[0 1 2 3 4] (5,)
[5 6 7 8 9] (5,)
>>> print(ar1,ar1.shape)
[[0 1 2 3 4]
[5 6 7 8 9]] (2, 5)
>>> a = np.array([[1],[2],[3]])
>>> b = np.array([['a'],['b'],['c'],['d']])
>>> ar2 = np.vstack((a,b)) #这里形状可以不一样。垂直(按行顺序)丢叠数组
>>> print(a,a.shape,'\n',b,b.shape)
[[1]
[2]
[3]] (3, 1)
[['a']
['b']
['c']
['d']] (4, 1)
>>> print(ar2,ar2.shape)
[['1']
['2']
['3']
['a']
['b']
['c']
['d']] (7, 1)
# numpy.vstack(tup):垂直(按行顺序)堆叠数组
>>> a = np.arange(5)
>>> b = np.arange(5,10)
>>> ar1 = np.stack((a,b))
>>> ar2 = np.stack((a,b),axis = 1)
>>> print(a,a.shape,'\n',b,b.shape)
[0 1 2 3 4] (5,)
[5 6 7 8 9] (5,)
>>> print(ar1,ar1.shape)
[[0 1 2 3 4]
[5 6 7 8 9]] (2, 5)
>>> print(ar2,ar2.shape)
[[0 5]
[1 6]
[2 7]
[3 8]
[4 9]] (5, 2)
numpy.stack(arrays, axis=0):沿着新轴连接数组的序列,形状必须一样!
- 重点解释axis参数的意思,假设两个数组[1 2 3]和[4 5 6],shape均为(3,0)
- axis=0:[[1 2 3] [4 5 6]],shape为(2,3)
- axis=1:[[1 4] [2 5] [3 6]],shape为(3,2)
>>> a = np.array([[1],[2],[3]]) #3行1列的二维数组
>>> b = np.array([['a'],['b'],['c']]) #3行1列的二维数组
>>> print(np.hstack((a,b))) #3行2列
[['1' 'a']
['2' 'b']
['3' 'c']]
>>> print(np.vstack((a,b))) #6行1列
[['1']
['2']
['3']
['a']
['b']
['c']]
>>> print(np.stack((a,b))) #shape为(2,3,1),每个元素表示相应的数组每一维的长度。ndim为3
[[['1']
['2']
['3']]
[['a']
['b']
['c']]]
>>> print(np.stack((a,b),axis = 0)) #默认为0,可不写。
[[['1']
['2']
['3']]
[['a']
['b']
['c']]]
>>> print(np.stack((a,b),axis = 1)) #.shape --> (3,2,1) ; .ndim ---> 3
[[['1']
['a']]
[['2']
['b']]
[['3']
['c']]]
2.5 数组拆分(np.hsplit( ar, n)垂直 np.vsplit(ar, n)水平拆分 )
>>> ar = np.arange(16).reshape(4,4)
>>> ar1 = np.hsplit(ar,2)
>>> print(ar)
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]]
>>> print(ar1,type(ar1))
[array([[ 0, 1],
[ 4, 5],
[ 8, 9],
[12, 13]]), array([[ 2, 3],
[ 6, 7],
[10, 11],
[14, 15]])] <class 'list'>
# numpy.hsplit(ary, indices_or_sections):将数组垂直(逐列)拆分为多个子数组 → 按列拆分
# 输出结果为列表,列表中元素为数组
>>> ar2 = np.vsplit(ar,4) >>> print(ar2,type(ar2)) [array([[0, 1, 2, 3]]), array([[4, 5, 6, 7]]), array([[ 8, 9, 10, 11]]), array([[12, 13, 14, 15]])] <class 'list'> >>>
# numpy.vsplit(ary, indices_or_sections)::将数组水平(行方向)拆分为多个子数组 → 按行拆
2.6 数组简单运算
(+ - * / ** mean() min() max() std() var() sum() sort() , axis=0按列/axis=1按行)
数组中的轴,在numpy中可以理解为方向,使用0,1,2数字表示,
- 对于一个1维数组,只有一个0轴;
- 对于一个2维数组(shape(2, 2))有0轴和1轴,
- 对于一个3维数组(shape(2,2,3))有0,1,2轴;
有了轴的概念,我们计算会更加方便,比如计算一个2维数组的平均值,必须指定计算哪个方向上面的数字的平均值。
二维数组的轴

三维数组的轴
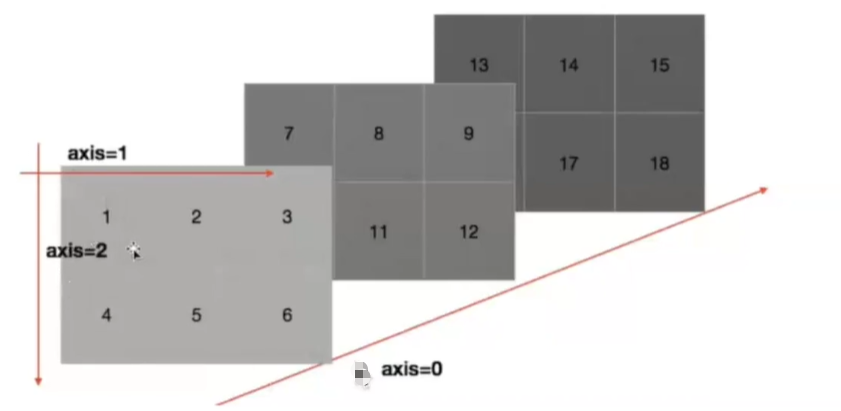
>>> ar = np.arange(6).reshape(2,3) >>> print(ar) [[0 1 2] [3 4 5]]
>>> print(ar + 10) #加法 [[10 11 12] [13 14 15]]
>>> print(ar * 2) #乘法 [[ 0 2 4] [ 6 8 10]]
>>> print(1 / (ar+1)) #除法 [[1. 0.5 0.33333333] [0.25 0.2 0.16666667]]
>>> print(ar ** 0.5) #幂法 [[0. 1. 1.41421356] [1.73205081 2. 2.23606798]] >>> print(ar.mean()) #求所有数据的平均值; np.mean(ar, axis=0)求某一行或某一列的平均值 2.5
>>> print(np.ptp(ar, axis=None)) #最大值和最小值的差;
>>> print(ar.max()) #求最大值; 求某一个轴上的数据最大值 np.max(ar, axis=0) 5 >>> print(ar.min()) #求最小值; 0 >>> print(ar.std()) #求标准差;标准差是一组数据平均值分散程度的一种度量。一个较大的标准差,代表大部分数值和其平均值之间差异较大;标准差小代表数据波动稳定。 1.707825127659933 >>> print(ar.var()) #求方差 2.9166666666666665 >>> print(ar.sum(),np.sum(ar,axis = 0)) #求和 np.sum()------>> axis = 0按列求和、axis = 1按行求和。 15 [3 5 7] >>> print(np.sort(np.array([1,4,3,2,5,6]))) #排序 [1 2 3 4 5 6]
# 数据的比较
# 第一个参数中的每一个数与第二个参数比较返回大的
print(np.maximum([-2, -1, 0, 1, 2], 0))
# [0 0 0 1 2]
# 第一个参数中的每一个数与第二个参数比较返回小的
print(np.minimum([-2, -1, 0, 1, 2], 0))
# [-2 -1 0 0 0]
# 接受的两个参数, 也可以大小一致; 第二个参数只是一个单独的值时, 其实是用到了维度的广播机制
print(np.maximum([-2, -1, 0, 6, 7], [1,2,3,4,5]))
# [1 2 3 6 7]
# 返回给定axis上的累计和
arr = np.array([[1,2,3], [4,5,6]])
print(arr, '\n', arr.cumsum(0))
'''
[1,2,3] ---> |1 |2 |3
[4,5,6] ---> |5=1+4|7=2+5|9=3+6
'''
print(arr.cumsum(1))
'''
[1,2,3] ---> |1 |2+1|3+2+1
[4,5,6] ---> |4 |4+5|4+5+6
'''
# argmin求最小值索引
print(np.argmin(arr, axis=0))
# [0 0 0]
扩展:方差var,协方差cov,计算平均值average, 计算中位数median
数组与数组之间的运算
不同形状的多维数组之间不能运算; 行数或者列数相同的一维数组和多维数组可以进行运算:
- 行形状相同(会与每一行数组的对应位相操作)
t1 = np.arange(24).reshape((4, 6))
t2 = np.arange(0, 6)
print(t1 - t2)
- 列形状相同(会与每一个相同维度的数组的对应位相操作)
t1 = np.arange(24).reshape((4, 6))
t2 = np.arange(4).reshape((4, 1))
print(t1 - t2)

数组的添加、删除和去重
① numpy.append 在数组的末尾添加值,追加操作会分配整个数组,并把原来的数组复制到新数组中。输入数组的维度必须匹配否则将生成valueError;
② numpy.insert 函数在给定索引之前,沿给定轴在输入数组中插入值;
如果值的类型转换为要插入,则它与输入数组不同。插入没有原地的,函数会返回一个新数组。此外,如果未提供轴,则输入数组会被展开;
③numpy.delete 函数返回从输入数组中删除指定子数组的新数组,与insert()函数类似的情况,如果未提供轴,则输入数组会被展开;
④ numpy.unique 用于去除数组中低端重复元素;
import numpy as np
a = np.array([[1,2,3], [4,5,6]])
print(a, '\n', np.append(a, [7,8,9])) #向数组添加元素
print('\n', np.append(a, [[7,8,9]], axis = 0)) #沿轴0 添加元素
print('\n', np.append(a, [[5,5,5],[7,8,9]], axis = 1)) #沿轴1 添加元素
----->>
[[1 2 3]
[4 5 6]]
[1 2 3 4 5 6 7 8 9]
[[1 2 3]
[4 5 6]
[7 8 9]]
[[1 2 3 5 5 5]
[4 5 6 7 8 9]]
#insert
a = np.array([[1,2], [3,4],[5,6]])
print(a, '\n', np.insert(a, 3, [11,12]))
# 沿轴0广播
print(np.insert(a, 1, [11], axis = 0))
# 沿轴1广播
print(np.insert(a, 1, [11], axis = 1))
---->>
[[1 2]
[3 4]
[5 6]]
[ 1 2 3 11 12 4 5 6]
[[ 1 2]
[11 11]
[ 3 4]
[ 5 6]]
[[ 1 11 2]
[ 3 11 4]
[ 5 11 6]]
#delete
a = np.arange(12).reshape(3,4)
# 未传递axis参数,则将会被展开
print(a, '\n', np.delete(a, 5))
# 删除每一行中的第二列
print(np.delete(a, 1, axis = 1))
---->>
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[ 0 1 2 3 4 6 7 8 9 10 11]
[[ 0 2 3]
[ 4 6 7]
[ 8 10 11]]
# unique
a = np.array([5,2,6,2,7,5,6,8,2,9])
# 第一个数组的去重值
print(a, '\n', np.unique(a))
# 去重数组的索引数组, return_index = True 返回新列表元素在旧列表中的位置(下标), 并以列表形式存储;
print(np.unique(a, return_index = True))
# 去重数组的下标, return_inverse = True 返回旧列表元素在新列表中的位置(下标), 并以列表形式存储
print(np.unique(a, return_inverse = True))
# return_counts = True 返回去重数组中的元素在原数组中的出现次数
print(np.unique(a, return_counts = True))
---->>
[5 2 6 2 7 5 6 8 2 9]
[2 5 6 7 8 9]
(array([2, 5, 6, 7, 8, 9]), array([1, 0, 2, 4, 7, 9], dtype=int64))
(array([2, 5, 6, 7, 8, 9]), array([1, 0, 2, 0, 3, 1, 2, 4, 0, 5], dtype=int64))
(array([2, 5, 6, 7, 8, 9]), array([3, 2, 2, 1, 1, 1], dtype=int64))
数组中nan和inf
C语言中表示最大值的正整数值是0X7FFF FFFF, 最小值的负整数是0x8000 0000,inf表示无穷大,需要使用float('inf')函数来转化,那么对应的就有float('-inf')表示无穷小了。这样就可以使用任意数来判断和它的
关系了。什么时候会出现inf呢? 比如一个数字除以0,python中会报错,但是numpy中会是一个inf或-inf;
另外还有nan,这种写法在pandas中常见,表示缺失的数据,所以一般用nan表示,任务与其做运算的结果都是nan。
import numpy as np
# 创建一个nan和inf
a = np.nan
b = np.inf
print(a, type(a))
# nan <class 'float'>
print(b, type(b))
# inf <class 'float'>
arr = np.arange(24, dtype = float).reshape(4,6)
# print(np.count_nonzero(arr)) # 判断非0的个数 23
print(arr)
arr[3,4] = np.nan
print(arr)
#print(np.count_nonzero(arr != arr)) #1 np.nan != np.nan 结果是TRUE
print(np.sum(arr, axis=0)) #nan和任何计算都为nan
arr[np.isnan(arr)] = 0
print(arr)
print(np.sum(arr, axis=0))
[[ 0. 1. 2. 3. 4. 5.]
[ 6. 7. 8. 9. 10. 11.]
[12. 13. 14. 15. 16. 17.]
[18. 19. 20. 21. 22. 23.]]
[[ 0. 1. 2. 3. 4. 5.]
[ 6. 7. 8. 9. 10. 11.]
[12. 13. 14. 15. 16. 17.]
[18. 19. 20. 21. nan 23.]]
[36. 40. 44. 48. nan 56.]
[[ 0. 1. 2. 3. 4. 5.]
[ 6. 7. 8. 9. 10. 11.]
[12. 13. 14. 15. 16. 17.]
[18. 19. 20. 21. 0. 23.]]
[36. 40. 44. 48. 30. 56.]
# 数组中的nan
import numpy as np
t = np.arange(24).reshape(4,6).astype('float')
t[1, 3:] = np.nan
print(t)
for i in range(t.shape[1]):
temp_col = t[:,i]
nan_num = np.count_nonzero(temp_col != temp_col)
if nan_num != 0:
temp_col_not_nan = temp_col[temp_col == temp_col]
temp_col[np.isnan(temp_col)] = np.mean(temp_col_not_nan)
print(t)
---->
[[ 0. 1. 2. 3. 4. 5.]
[ 6. 7. 8. nan nan nan]
[12. 13. 14. 15. 16. 17.]
[18. 19. 20. 21. 22. 23.]]
[[ 0. 1. 2. 3. 4. 5.]
[ 6. 7. 8. 13. 14. 15.]
[12. 13. 14. 15. 16. 17.]
[18. 19. 20. 21. 22. 23.]]
3. Numpy索引及切片
ar[2]、 ar[3][1] 、 ar[3, 1] 、 ar[1: 3] 、 ar[:2 , 1:] 切片为数组中的第1、2行,第2、3、4列。
指定新数组为一列:reshape(-1,1); 指定新数组为一行:reshape(1,-1)
#一维数组基本索引及切片
#冒号分割切片参数 start: stop: step 来进行切片操作
>>> ar = np.arange(20) >>> print(ar) [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19]
>>> print(ar[2:7:2]) #从索引2开始到索引7停止,间隔为2;
>>> print(ar[2:]) #从索引开始以后的所有项都将被提取; >>> print(ar[4]) 4 >>> print(ar[3:6]) [3 4 5]
#二维数组索引及切片 >>> ar = np.arange(16).reshape(4,4) >>> print(ar,'数组轴数为%i'%ar.ndim) #4*4的数组 [[ 0 1 2 3] [ 4 5 6 7] [ 8 9 10 11] [12 13 14 15]] 数组轴数为2
>>> print(ar[2], '数组轴数为%i'%ar[2].ndim) #取一行,切片为下一个维度的一个元素,所以为一维数组。 [ 8 9 10 11] 数组轴数为1 >>> print(ar[2][1]) #二次索引,得到一维数组中的一个值; 9 >>> print(ar[1:3], '数组轴数为%i'%ar[1:3].ndim) #取连续的多行,切片为2个一维数组组成的二维数组; [[ 4 5 6 7] [ 8 9 10 11]] 数组轴数为2 >>> print(ar[2,2]) #切片为数组中的第3行第3列; 10 >>> print(ar[:2 , 1:]) #切片为数组中的第1、2行,第2、3、4列;二维数组 [[1 2 3] [5 6 7]]
# 三维数组索引及切片
>>> ar = np.arange(8).reshape(2,2,2) >>> print(ar, '数组轴数为%i'%ar.ndim) #2*2*2的数组; [[[0 1] [2 3]] [[4 5] [6 7]]] 数组轴数为3 >>> print(ar[0], '数组轴数为%i'%ar[0].ndim) #三维数组的下一个维度的第一个元素 ----->> 一个二维数组; [[0 1] [2 3]] 数组轴数为2 >>> print(ar[0][0], '数组轴数为%i'%ar[0][0].ndim) #三维数组的下一个维度的第一个元素下的第一个元素 ------>> 一个一维数组 [0 1] 数组轴数为1 >>> print(ar[0][0][1], '数组轴数为%i'%ar[0][0][1].ndim) 1 数组轴数为0
布尔型索引及切片
用布尔型矩阵进行筛选 、用判断矩阵做筛选
>>> ar = np.arange(12).reshape(3,4) >>> i = np.array([True,False,True]) >>> j = np.array([True,True,False,False]) >>> print(ar,'\n',i,'\n',j) [[ 0 1 2 3] [ 4 5 6 7] [ 8 9 10 11]] [ True False True] [ True True False False] >>> print(ar[i,:]) #在第一维度做判断,只保留True,这里第一维度是指行,ar[i,:]等同于ar[i](简单书写格式);索引[i,:] i代表行索引,:代表列索引全部都有 [[ 0 1 2 3] [ 8 9 10 11]] >>> print(ar[:,j]) #在第二维度即按列去做判断,这里ar[:,j]就不等同于ar[j]了 。 [[0 1] [4 5] [8 9]]
#布尔型索引:以布尔型的矩阵去做筛选
>>> m = ar > 5 >>> print(m) #这里m是一个判断矩阵; [[False False False False] [False False True True] [ True True True True]] >>> print(ar[m]) #用m判断矩阵去筛选ar数组中>5的元素 ------------->>>后边pandas判断方式的原理就在此。 [ 6 7 8 9 10 11]
数组索引及切片的值更改、复制
>>> ar = np.arange(10) >>> print(ar) [0 1 2 3 4 5 6 7 8 9] >>> ar[5] = 100 >>> ar[7:9] = 200 >>> print(ar) [ 0 1 2 3 4 100 6 200 200 9] >>>
##一个标量赋值给一个索引/切片时,会自动改变/传播原始数组
>>> ar = np.arange(10) >>> b = ar.copy() >>> b[7:9] = 200 >>> print(ar) [0 1 2 3 4 5 6 7 8 9] >>> print(b) [ 0 1 2 3 4 5 6 200 200 9] >>>
#复制
4. Numpy随机数
随机数生成
####生成一个标准正太分布的4*4样本值
>>> samples = np.random.normal(size=(4,4)) #random.normal就表示正态分布 >>> print(samples) [[ 0.07060943 -1.25339552 0.29914172 -0.5340139 ] [-0.48759624 -0.59666746 -0.11825987 0.04588257] [-0.43502379 -0.29065528 0.17958867 -1.61939862] [ 0.06733506 0.11634428 0.05324929 -0.46936231]]
numpy.random.rand(d0, d1, ..., dn):生成一个[0,1)之间的随机浮点数或N维浮点数组 —— 均匀分布
以给定的形状创建一个数组,并在数组中加入在[0,1]之间均匀分布的随机样本
>>> a = np.random.rand() >>> print(a,type(a)) #生成一个随机浮点数 0.34655619552666683 <class 'float'> >>> >>> b = np.random.rand(4) >>> print(b,type(b)) #生成形状为4的一维数组 [0.97735994 0.20438528 0.5741046 0.6604635 ] <class 'numpy.ndarray'> >>> c = np.random.rand(2,3) >>> print(c,type(c)) #生成形状为2*3的二维数组,注意这里不是((2,3)) [[0.75476081 0.30673306 0.94664526] [0.4011794 0.91558286 0.09614256]] <class 'numpy.ndarray'> >>>
#####在Jupyter里边运行
samples1 = np.random.rand(500) samples2 = np.random.rand(500) import matplotlib.pyplot as plt % matplotlib inline
# 生成500个均匀分布的样本值
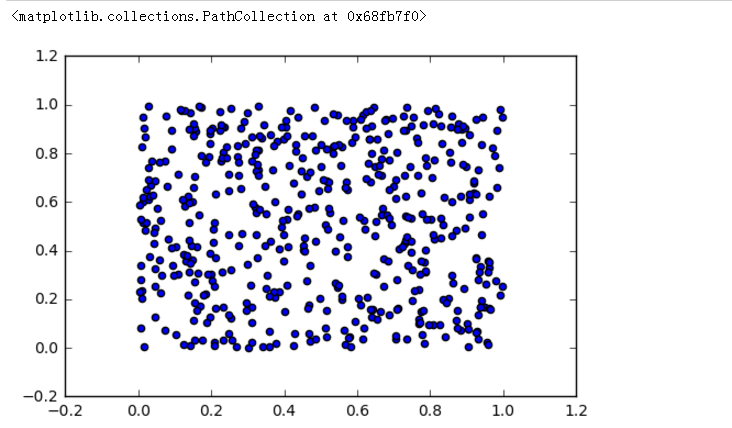
numpy.random.randn(d0, d1, ..., dn):生成一个浮点数或N维浮点数组 —— 正态分布;
以给定的形状创建一个数组,数组元素来符合标准正态分布N(0,1) ;若要获得一般正态分布
samples1 = np.random.randn(500)
samples2 = np.random.randn(500)
import matplotlib.pyplot as plt
% matplotlib inline
plt.scatter(samples1,samples2)
# randn和rand的参数用法一样
# 生成1000个正太的样本值
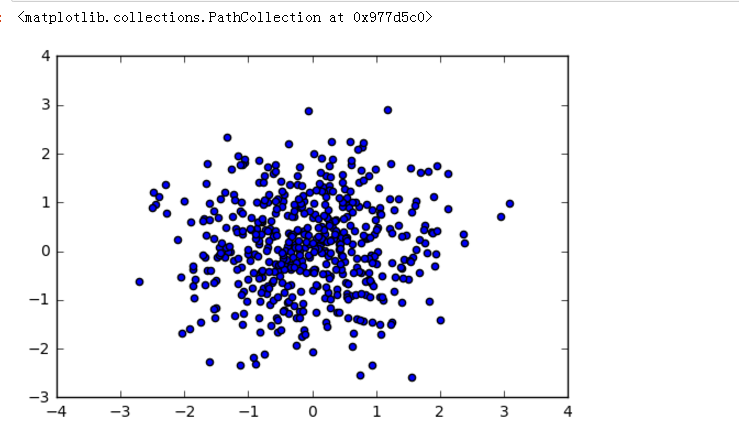
numpy.random.randint(low, high=None, size=None, dtype='l'):生成一个整数或N维整数数组
# 若high不为None时,取[low,high)之间随机整数,否则取值[0,low)之间随机整数,且high必须大于low
# dtype参数:只能是int类型
>>> print(np.random.randint(2)) ## low=2:生成1个[0,2)之间随机整数
0
>>> print(np.random.randint(2,size = 5)) #low=2,size=5 :生成5个[0,2)之间随机整数
[1 1 0 0 0]
>>> print(np.random.randint(2,6,size=5)) #low=2,high=6,size=5:生成5个[2,6)之间随机整数
[2 4 2 5 4]
>>> print(np.random.randint(2,size=(2,3))) #low=2,size=(2,3):生成一个2x3整数数组,取数范围:[0,2)随机整数
[[0 1 1]
[1 0 0]]
>>> print(np.random.randint(2,6,(2,3))) #low=2,high=6,size=(2,3):生成一个2*3整数数组,取值范围:[2,6)随机整数
[[5 3 3]
[3 2 2]]
5. Numpy数据的输入输出
存储数组数据 .npy文件
import os
os.chdir(r'C:\Users\Administrator\Desktop')
ar = np.random.rand(5,5)
print(ar)
# np.save('arraydata.npy',ar)
np.save(r'C:\Users\Administrator\Desktop\arraydata.npy',ar)
print('finish')
打印:
[[ 0.26757585 0.29147944 0.64875451 0.93792551 0.94136359]
[ 0.26270971 0.11359578 0.40340343 0.43775798 0.00448808]
[ 0.77723808 0.67647676 0.01720309 0.1811023 0.5937187 ]
[ 0.64925335 0.76782983 0.07480746 0.54560242 0.34152663]
[ 0.77761772 0.67317061 0.61600948 0.58411754 0.61670874]]
finish
读取数组数据 .npy文件
ar_load = np.load('arraydata.npy')
print(ar_load)
#np.load(r'C:\Users\Administrator\Desktop\arraydata.npy') ##也可以直接打开
[[ 0.26757585 0.29147944 0.64875451 0.93792551 0.94136359]
[ 0.26270971 0.11359578 0.40340343 0.43775798 0.00448808]
[ 0.77723808 0.67647676 0.01720309 0.1811023 0.5937187 ]
[ 0.64925335 0.76782983 0.07480746 0.54560242 0.34152663]
[ 0.77761772 0.67317061 0.61600948 0.58411754 0.61670874]]
存储/读取文本文件
ar = np.random.rand(5,5)
np.savetxt('array.txt',ar,delimiter=',')
# np.savetxt(fname, X, fmt='%.18e', delimiter=' ', newline='\n', header='', footer='', comments='# '):存储为文本txt文件
ar_loadtxt = np.loadtxt('array.txt',delimiter=',') ##delimiter=','是以,进行分隔
print(ar_loadtxt)
# 也可以直接 np.loadtxt(r'C:\Users\Administrator\Desktop\array.txt')
[[ 0.85083698 0.67495645 0.95420959 0.29894536 0.85662616]
[ 0.2238608 0.31017771 0.58716182 0.48031634 0.65689202]
[ 0.79469571 0.32661995 0.99651714 0.1758829 0.01264854]
[ 0.75023541 0.10395296 0.69800992 0.23672871 0.00297461]
[ 0.828437 0.67540604 0.92137268 0.652755 0.23985235]]


