因子分解机 libFM| DeepFM| Deep&wide| NFM
1. 因子分解机
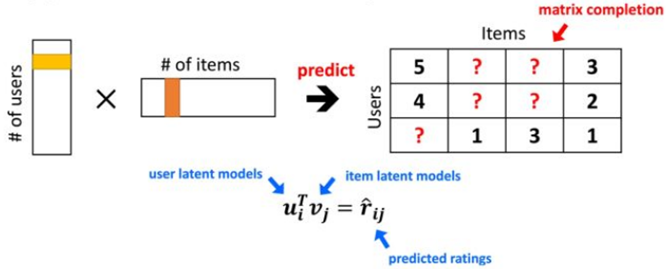
MF的回顾
矩阵分解:
- 将矩阵拆解为多个矩阵的乘积
- 用户users和商品Items的评分矩阵是稀疏的,因为他不会对所有商品打分;把它拆分为2部分,K值是降维的维度,比如user1对10w个电影打分,10w降为K维(K一般取100左右);
- k维降维变成稠密矩阵;
矩阵分解方法:
- EVD(特征值分解)
- SVD(奇异值分解)
求解近似矩阵分解的最优化问题
- ALS(交替最小二乘法):ALS-WR
- SGD(随机梯度下降):FunkSVD, BiasSVD, SVD++
- 奇异值分解可以对矩阵进行无损分解
- 在实际中,我们可以抽取前K个特征,对矩阵进行降维
- SVD在降维中有效,抽取不同的K值(10%的特征包含99%的信息)
- 在评分预测中使用funkSVD,只根据实际评分误差进行目标最优化
- 在funkSVD的基础上,加入用户/商品偏好 => BiasSVD
- 在BiasSVD的基础上,考虑用户的隐式反馈 => SVD++
- 以上的MF,我们都只考虑user和item特征,但实际上一个预测问题包含的特征维度可能很多
MF局限性
什么是预测问题:
- 在机器学习中,可以把预测问题看成是估计一个函数

- n维实特征向量 映射到目标域T,对于训练集,
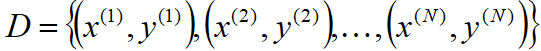
- 回归问题:T为实数
- 二分类问题:T为{0,1}
- n的维度往往很大,不只是二维,即userID, itemID
对于电影评分系统,特征维度也不仅仅是userID, itemID,还有其他维度:
- S={(A, TI, 2010-1, 5), #用户和电影之间 时间维度也很重要
- (A, NH, 2010-2, 3),
- (A, SW, 2010-4, 1),
- (B, SW, 2009-5, 4),
- (B, ST, 2009-8, 5),
- (C, TI, 2009-9, 1),
- (C, SW, 2009-12, 5),
- ...
- }
U={Alice(A), Bob(B), Charlie(C), ...}
I={Titanic(TI), Notting Hill(NH), Star Wars(SW), Star Trek(ST),...}
用户在什么时间,对哪部电影,打了多少分
我们需要预测y',即某个用户,在某个时刻,对某个电影的打分

构建两两交互打分;
蓝色部分:当前评分用户信息
红色部分:当前被评分电影
黄色:当前评分用户,评分过的其他电影
绿色:评分时间(按照2009年1月开始的间隔月数)
棕色:用户评分过的上一部电影
FM算法
FM 就相当于是for 循环里的矩阵分解,两两之间组合(原来的矩阵分解只定义了2个特征);
线性回归:
- 对于特征向量
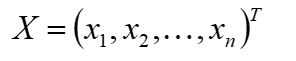
- 目标预估函数
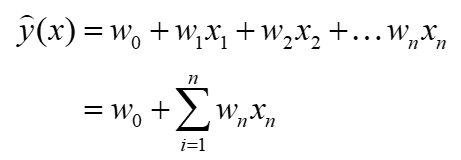
-
- 认为变量之间是相互独立的,没有考虑变量之间的相互关系,比如性别+年龄的组合
- 对于二阶表达式:

-
- 二阶特征组合:考虑了两个特征变量之间的交互影响
- 使用Wij进行二阶特征组合的参数估计存在问题,即如果观察样本中没有出现过该交互的特征分量,那么直接估计将为0
对于Wij的估计,转换成了矩阵分解MF问题

直接计算,复杂度为O(k*n^2) ;n是特征个数,k是特征的embedding size

FM与MF的区别
- FM矩阵将User和Item都进行了one-hot编码作为特征,使得特征维度非常巨大且稀疏
- 矩阵分解MF(例子中只有2个维度)是FM的特例,即特征只有User ID 和Item ID的FM模型;MF只考虑了UserID, ItemID的特征,而实际我们需要考虑更多的特征,甚至是多个特征之间的组合;
- 矩阵分解MF只适用于评分预测问题,进行简单的特征计算,无法利用其他特征,而实际问题可能是回归和分类问题 需要更通用的解决方式;
- FM引入了更多辅助信息(Side information)作为特征,FM考虑了更多特征以及二阶特征组合,可以作为通用的回归和分类算法;
- FM在计算二阶特征组合系数的时候,使用了MF
- 特征提取是对现实世界的拟合方式

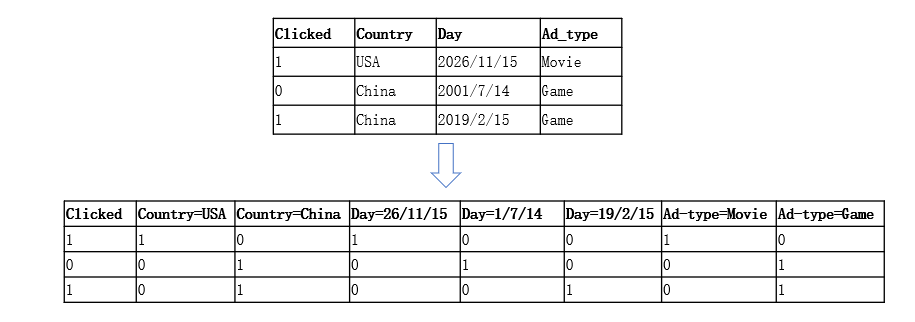
FM中的特征交叉:
- CTR(Click Through Rate)预估是个二分类问题
- 线性模型无法学习到特征之间的相关性,比如“ Country=USA” +“Day=26/11/15” ,“ Country=China”+“Day=19/2/15”,对用户的Click有正面影响
FM的学习算法:
- ALS,交替最小二乘法
- SGD,随机梯度下降法
-
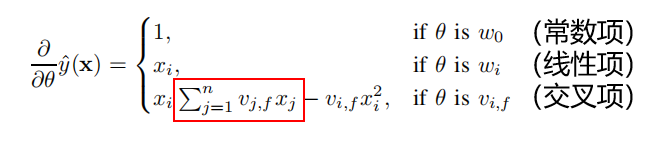
- 可以提前计算(与i无关),因此梯度的计算复杂度为O(1),参数更新的计算复杂度为O(k*n)
- MCMC,马尔科夫链蒙特卡罗法
D-阶FM算法:
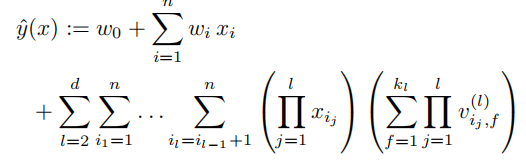
- 因为计算量大,一般FM采用2阶特征组合的方式
- 实际上高阶/非线性的特征组合适合采用深度模型
- Wij = <Vi, Vj>是FM的核心思想,使得稀疏数据下学习不充分的问题也能得到充分解决 => 可提供的非零样本大大增加
FM算法的应用场景:
- 回归问题,y'(x)直接作为预测值,损失函数可采用least square error
- 二分类问题,FM的输出还需要经过 sigmoid 函数变换,也就是将y'(x)转化为二分类标签,即0,1:

y(i)是真实样本的类别标记,正样本为1,负样本为0,m为样本总数
损失函数可采用logistic loss
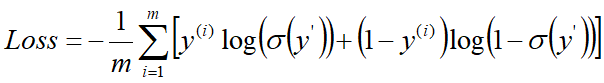
libFM
libFM(FM软件)
- 下载地址:https://github.com/srendle/libfm
- 使用文档:http://www.libfm.org/libfm-1.42.manual.pdf
- FM论文作者Steffen Rendle提供的工具(2010年)
- 在KDD CUP 2012,以及Music Hackathon中都取得不错的成绩
- 不仅适用于推荐系统,还可以用于机器学习(分类问题)
- 实现三种优化算法:SGD,ALS,MCMC
- 支持2种输入数据格式:文本格式(推荐)和二进制格式
libFM数据格式
- 每一行都包含一个训练数据(x,y),首先规定y的值,然后是x的非零值。
- 对于二分类问题,y>0的类型被认为是正分类,y<=0被认为是负分类。

3个样本,7个维度,y值 ;进行数据格式转换,y放前边,把有的值放进去即可;
使用libFM自带的libsvm格式转换
- triple_format_to_libfm.pl (perl文件)
- -target 目标变量
- -delete_column 不需要的变量
- perl triple_format_to_libfm.pl -in ratings.dat -target 2 -delete_column 3 -separator "::"
- 自动将.dat文件 => .libfm文件
使用libFM训练FM模型
- -train 指定训练集,libfm格式或者二进制文件
- -test 指定测试集,libfm格式或者二进制文件
- -task,说明任务类型classification还是regression
- dim,维度 指定k0,k1,k2,
- -iter,迭代次数,默认100
- -method,优化方式,可以使用SGD, SGDA, ALS, MCMC,默认为MCMC
- -out,指定输出文件
- libFM -task r -train ratings.dat.libfm -test ratings.dat.libfm -dim '1,1,8' -out out.txt
使用libFM进行分类
- Titanic数据集,train.csv和test.csv
- Step1,对train.csv和test.csv进行处理
- 去掉列名,针对test.csv增加虚拟target列(值设置为1)
- Step2,将train.csv, test.csv转换成libfm格式
- perl triple_format_to_libfm.pl -in ./titanic/train.csv -target 1 -delete_column 0 -separator ","
- perl triple_format_to_libfm.pl -in ./titanic/test.csv -target 1 -delete_column 0 -separator ","
- Titanic数据集,train.csv和test.csv
- Step3,使用libfm进行训练,输出结果文件 titanic_out.txt
- libFM -task c -train ./titanic/train.csv.libfm -test ./titanic/test.csv.libfm -dim '1,1,8' -out titanic_out.txt
FFM算法
FM无法区分出来是哪个特征列 field;
- Field-aware Factorization Machines for CTR Prediction
- https://www.csie.ntu.edu.tw/~cjlin/papers/ffm.pdf
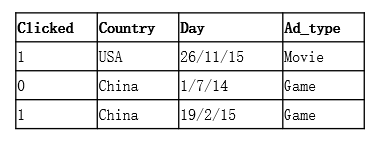
- 通过引入field的概念,FFM把相同性质的特征归于同一个field,比如“Day=26/11/15”、“Day=1/7/14”、“Day=19/2/15”这三个特征代表日期,放到同一个field中
- 当“Day=26/11/15”与Country特征,Ad_type特征进行特征组合时,使用不同的隐向量(Field-aware),这是因为Country特征和Ad_type特征,本身的field不同
对于FM算法:
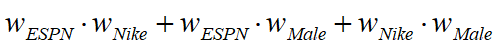
- 每个特征有唯一的一个隐向量表示,这个隐向量被用来学习与其他任何特征之间的影响。
- w(ESPN)用来学习与Nike的隐性影响w(ESPN)*w(Nike),同时也用来学习与Male的影响w(ESPN)*w(Male)。但是Nike和Male属于不同的领域,它们的隐性影响(latent effects)应该是不一样的。
- 对于FFM算法:
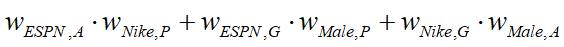
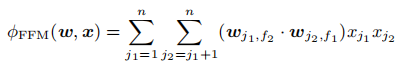
- 每个特征会有几个不同的隐向量,fj 是第 j 个特征所属的field
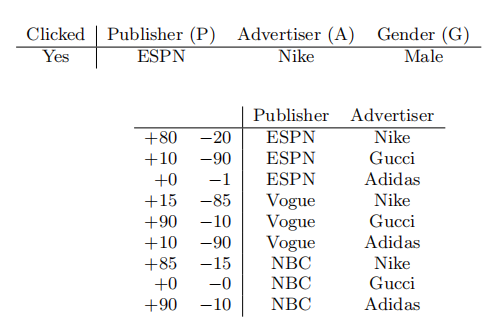
FM算法:
- 每个特征只有一个隐向量
- FM是FFM的特例
FFM算法
- 每个特征有多个隐向量
- 使用哪个,取决于和哪个向量进行点乘
FM的特点是 可以有2个特征项x1,x2,WESPN和WNIKE 可以做交叉学习,把之前没有学到的学出来;
FFM也要两两组合,学到的参数量更大了,它带有了方向看是跟谁去做交叉组合;

FFM算法:

- 隐向量的长度为 k,FFM的二次参数有 nfk 个,多于FM模型的 nk 个
- 由于隐向量与field相关,FFM二次项并不能够化简,计算复杂度是 O(k*n^2),FFM的k值一般远小于FM的k值; 特征格式:field_id:feat_id:value
- field_id代表field编号,feat_id代表特征编号,value是特征值。
- 如果特征为数值型,只需分配单独的field编号,比如评分,item的历史CTR/CVR等。
- 如果特征为分类(categorical)特征,需要经过One-Hot编码成数值型,编码产生的所有特征同属于一个field。特征值是0或1,比如性别、商品的品类id等

FFM的输入格式
有几个field就是原数特征有几列,4个field,5个特征feature;

libFFM
- https://github.com/ycjuan/libffm
xlearn
- https://xlearn-doc-cn.readthedocs.io/en/latest/index.html
- 提供Python接口
- 支持LR,FM,FFM算法等
- 运行效率高,比libfm, libffm快
criteo_ctr数据集
- 展示广告CTR预估比赛
- 欧洲大型重定向广告公司Criteo的互联网广告数据集(4000万训练样本,500万测试样本)
- 原始数据:https://labs.criteo.com/2013/12/download-terabyte-click-logs/
- small_train.txt 和 small_test.txt文件
- (FFM数据格式,200条记录)
import xlearn as xl # 创建FFM模型 ffm_model = xl.create_ffm() # 设置训练集和测试集 ffm_model.setTrain("./small_train.txt") ffm_model.setValidate("./small_test.txt") # 设置参数,任务为二分类,学习率0.2,正则项lambda: 0.002,评估指标 accuracy param = {'task':'binary', 'lr':0.2, 'lambda':0.002, 'metric':'acc'} # FFM训练,并输出模型 ffm_model.fit(param, './model.out') # 设置测试集,将输出结果转换为0-1 ffm_model.setTest("./small_test.txt") ffm_model.setSigmoid() ffm_model.predict("./model.out", "./output.txt")
xlearn工具输入数据格式:
LR ,FM 算法: CSV 或者 libsvm
FFM 算法:libffm 格式
DeepFM算法
DeepFM算法:
- DeepFM: A Factorization-Machine based Neural Network for CTR Prediction,2017
- https://arxiv.org/abs/1703.04247
- FM可以做特征组合,但是计算量大 (kn^d),一般只考虑2阶特征组合
- 如何既考虑低阶(1阶+2阶),又能考虑到高阶特征 => DeepFM=FM+DNN
- 设计了一种end-to-end的模型结构 => 无须特征工程
- 在各种benchmark和工程中效果好
- Criteo点击率预测, 4500万用户点击记录,90%样本用于训练,10%用于测试
- Company*游戏中心,10亿记录,连续7天用户点击记录用于训练,之后1天用于测试
DeepFM = FM + DNN:
- 提取低阶(low order)特征 => 因子分解机FM
- 既可以做1阶特征建模,也可以做2阶特征建模
- 提取高阶(high order)特征 => 神经网络DNN
- end-to-end,共享特征输入
- 对于特征i,wi是1阶特征的权重,
- Vi表示该特征与其他特征的交互影响,输入到FM模型中可以获得特征的2阶特征表示,输入到DNN模型得到高阶特征。
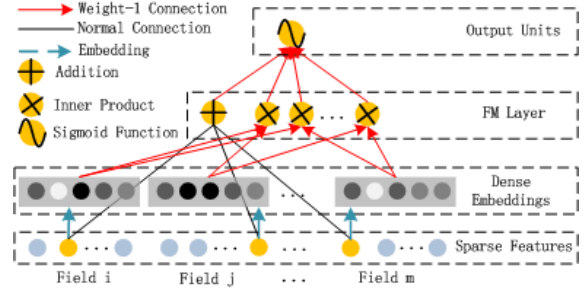
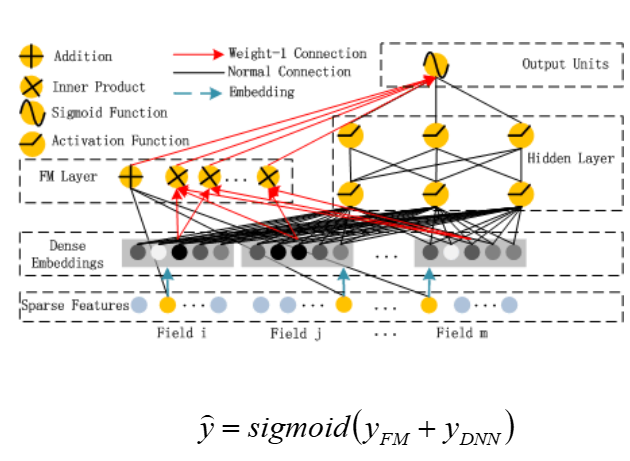
下图 左侧为FM、右侧为DNN,原始数据Sparse Features 稀疏项 做one hot编码,通过Embedding进行稠密化 (如果维度很大喂给DNN 会维度爆炸 影响收敛);
左侧做低阶机器学习,右侧做深度学习,同一份数据做两个模型的训练,两路大军yFM和 yDNN 汇合;
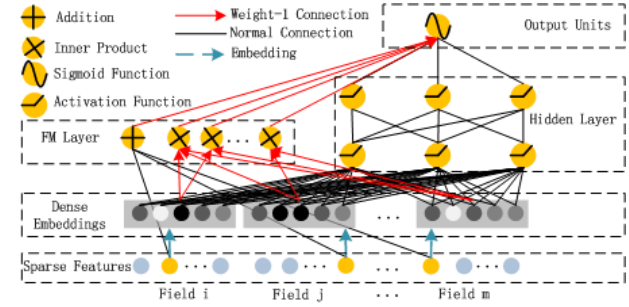
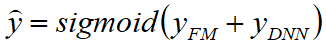
FM模型
- 1阶特征建模
- 通过隐向量点乘 => 得到2阶特征组合
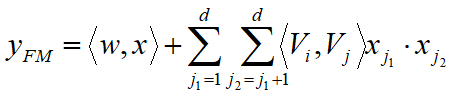
Deep模型
- 原始特征向量维度非常大,高度稀疏,为了更好的发挥DNN模型学习高阶特征的能力,设计子网络结构(从输入层=>嵌入层),将原始的稀疏表示特征映射为稠密的特征向量。
- Input Layer (one hot编码 如1w维)=> Embedding Layer (Embedding site 比如为100,)
- 不同field特征长度不同,但是子网络输出的向量具有相同维度k
- 利用FM模型的隐特征向量V作为网络权重初始化来获得子网络输出向量
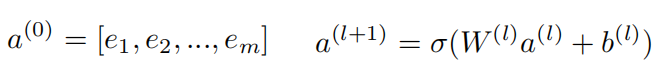
从稀疏到稠密,是一个嵌入的过程,
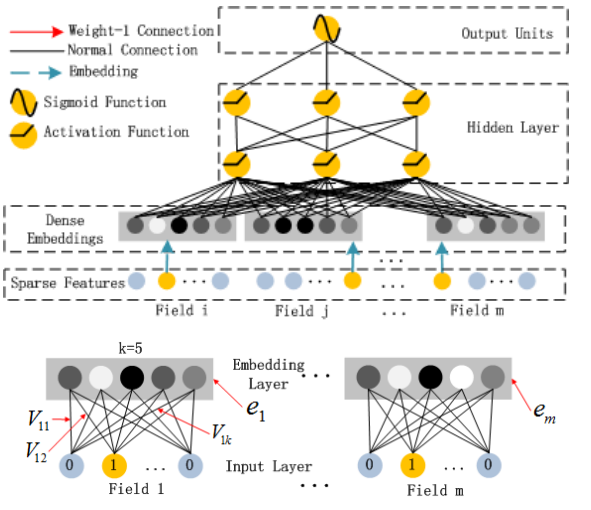
什么是Embedding:
- 一种降维方式,将不同特征转换为维度相同的向量
- 在推荐系统中,对于离线变量我们需要转换成one-hot => 维度非常高,可以将其转换为embedding向量
- 原来每个Field i维度很高,都统一降成k维embedding向量
- 方法:接入全连接层,对于每个Field只有一个位置为1,其余为0,因此得到的embedding就是图中连接的红线,对于Field 1来说就是 V11, V12, V13,...V1K
- FM模型和Deep模型中的子网络权重共享,也就是对于同一个特征,向量Vi是相同的

DeepFM中的模块:
- Sparse Features,输入多个稀疏特征
- Dense Embeddings
- 对每个稀疏特征做embedding,学习到他们的embedding向量(维度相等,均为k),因为需要将这些embedding向量送到FM层做内积。同时embedding进行了降维,更好发挥Deep Layer的高阶特征学习能力
- FM Layer
- 一阶特征:原始特征相加
- 二阶特征:原始特征embedding后的embedding向量两两内积
- Deep Layer,将每个embedding向量做级联,然后做多层的全连接,学习更深的特征
- Output Units,将FM层输出与Deep层输出进行级联,接一个dense层,作为最终输出结果
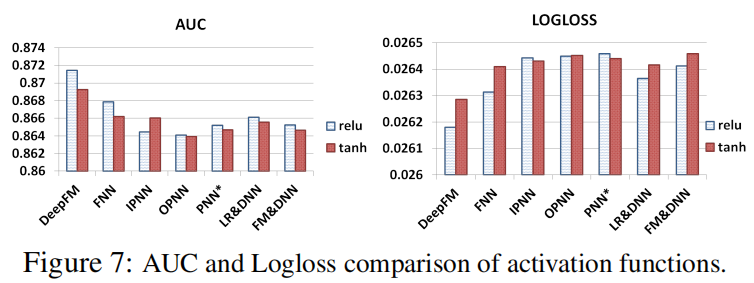
激活函数
- relu和tanh比sigmoid更适合
- relu对于所有深度模型来说更适合
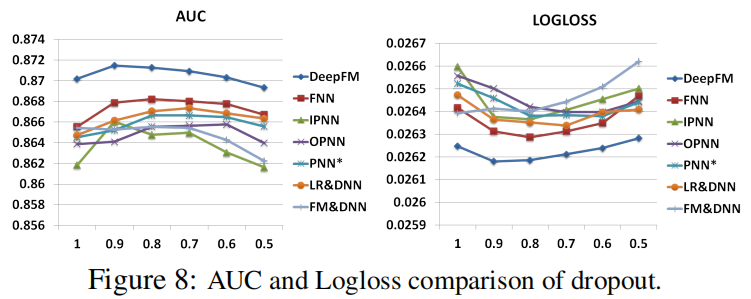
Dropout
- 设置为0.6-0.9之间最适合
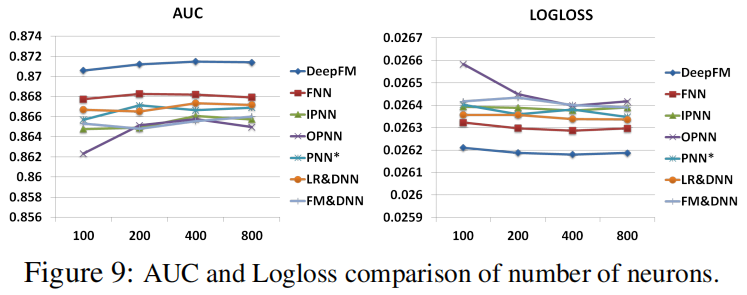
神经元个数
- 每层的神经元个数越多,未必越好
- 设置为200-400个比较适合
隐藏层层数
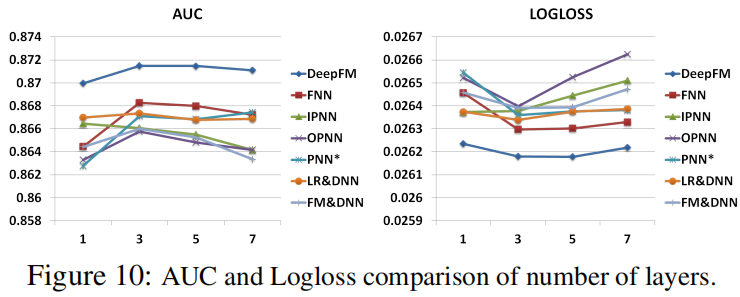
- 层数越多,起初效果明显,之后效果不明显,甚至更差,容易过拟合
- 3层比较适合
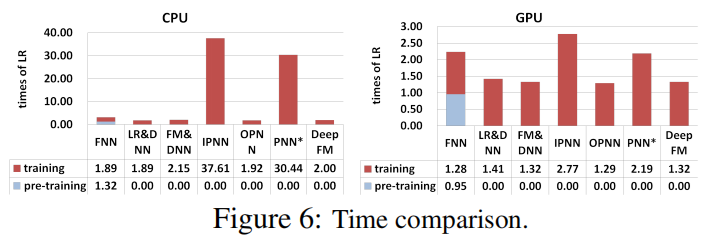
执行时间
- 不论是CPU还是GPU,DeepFM的执行时间都是最短的
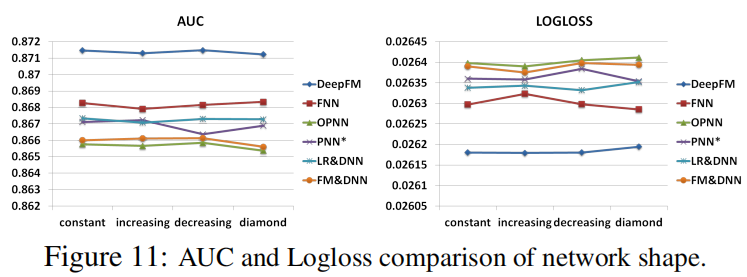
网络形状
- 固定(200-200-200),增长(100-200-300), 下降(300-200-100), 菱形(150-300-150).
- 采用固定的形状效果最好
Wide & Deep算法
Wide & Deep模型
- 论文:Wide & Deep Learning for Recommender Systems,2016 https://arxiv.org/abs/1606.07792
- 推荐系统的挑战是 memorization与generalization
- memorization,记忆能力(wide是LR),学习items或者features之间的相关频率,在历史数据中探索相关性的可行性
- generalization,泛化(推理)能力(deep),基于相关性的传递,去探索一些在过去没有出现过的特征组合
- 结合线性模型的记忆能力和DNN模型的泛化能力,在训练过程中同时优化两个模型的参数

Wide推荐
- 系统通过获得用户的购物日志数据,包括用户点击哪些商品,购买过哪些商品,然后通过OneHot编码转换为离散特征
- 好处是可解释性强,不足在于特征组合需要人为操作
Deep推荐
- 通过深度学习出一些向量,这些向量是隐性特征,往往没有可解释性的
两个模型融合的方法
- ensemble:两个模型分别对全量数据进行预测,然后根据权重组合最终的预测结果
- joint training:wide和deep的特征合一,构成一个模型进行预测
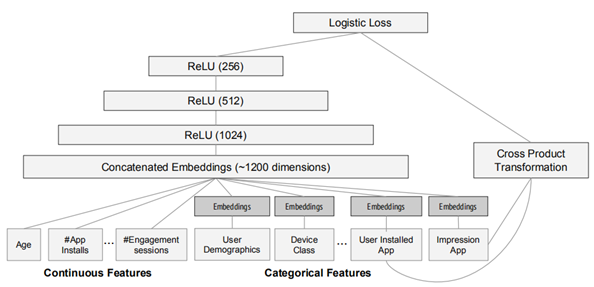
Wide推荐
- 采用Linear Regression,特征组合需要人来设计一个有d个特征的样本 X = [x1, x2, x3,...xd ]
- 模型的参数 W = [w1, w2, w3,...wd]
- 线性回归 y =WT X + b
- 实际中往往需要交叉特征
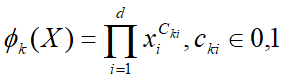
- 最终Wide模型
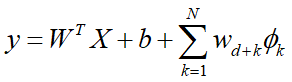
wide模型是线性模型,输入特征可以是连续特征,也可以是稀疏的离散特征。离散特征通过交叉可以组成更高维的离散特征。
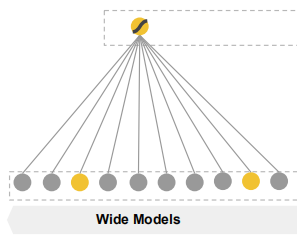
Deep推荐
Deep模型使用的特征:连续特征,Embedding后的离散特征,
使用前馈网络模型,特征首先转换为低维稠密向量,作为第一个隐藏层的输入,解决维度爆炸问题
根据最终的loss反向训练更新。向量进行随机初始化,隐藏层的激活函数通常使用ReLU
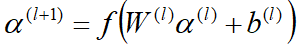
Wide模型使用的特征:Cross Product Transformation生成的组合特征,但无法学习到训练集中没有出现的组合特征
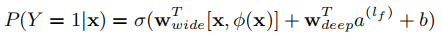
- 代表X的Cross Product Transformation
- 代表Wide模型的权重向量
- 代表Deep模型的权重向量
- 代表最终的神经网络数结果,b为偏差
Wide join Deep
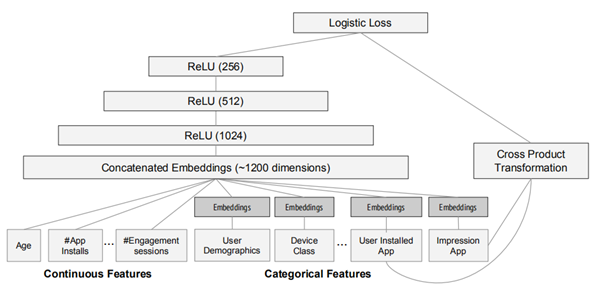
Google在2016年基于TensorFlow发布的用于分类和回归的模型,并应用到了 Google Play 的应用推荐中 ;
Wide & Deep模型不论在线下还是线上相比于单独的wide模型和单独的Deep模型,效果都有明显提升。
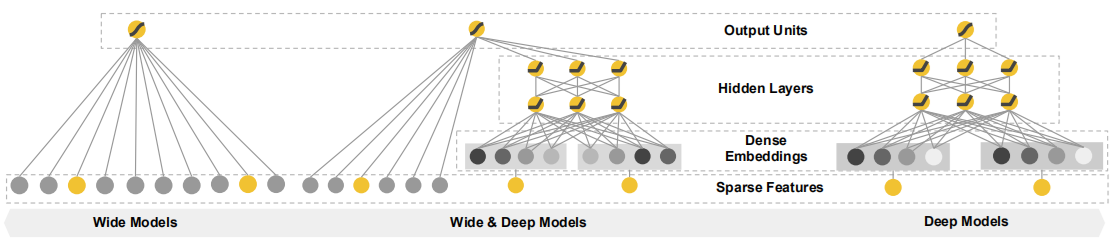
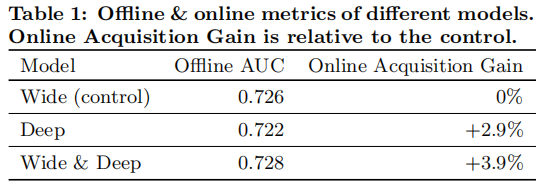
NFM算法
FNN, Wide & Deep, DeepFM都是在DNN部分,对embedding之后的特征进行concatenate,没有充分进行特征交叉计算。
NFM算法是对embedding直接采用对位相乘(element-wise)后相加起来作为交叉特征,然后通过DNN直接将特征压缩,最后concatenate linear部分和deep部分的特征。
两种FM和DNN的结合方式:
- DeepFM, 并行结构,FM和DNN分开计算
- NFM,串行架构,将FM的结果作为DNN的输入
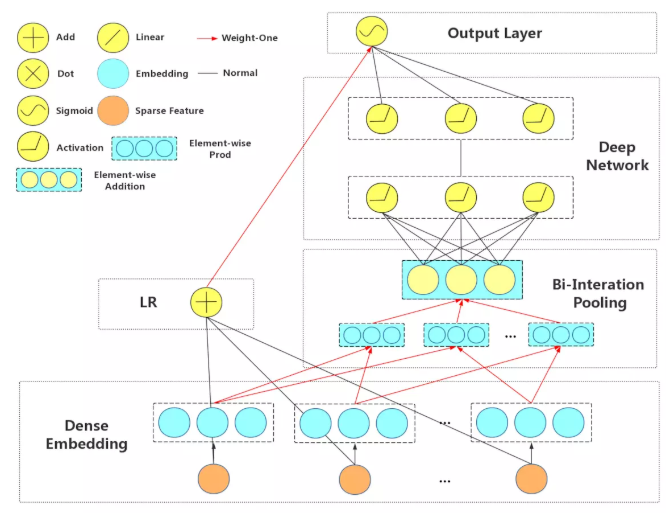
NFM模型
- 对于输入X的预测公式:

- Embedding层:全连接层,将稀疏输入映射到一个密集向量,得到 Vx = {x1v1, x2v2, ... xnvn }
- BI层: 池化操作,将一系列的Embedding向量转换为一个向量

- 隐藏层:神经网络的全连接层
- 预测层:将隐藏层输出到n*1的全连接层, Vx = {x1v1, x2v2, ... xnvn }
- 得到预测结果
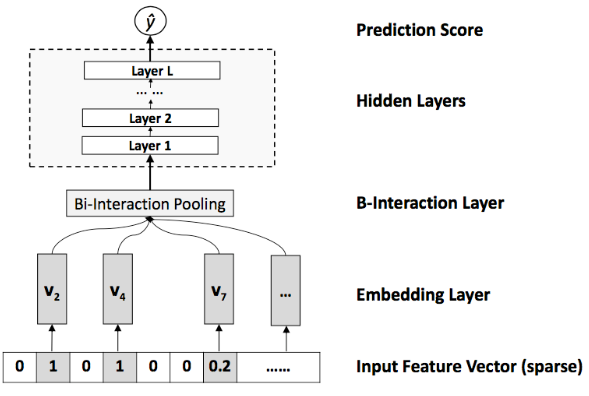
NFM模型
FM 通过隐向量完成特征组合工作,同时解决了稀疏的问题。但是 FM 对于 non-linear 和 higher-order 特征交叉能力不足,因此可以使用FM和DNN来弥补这个不足 => NFM
BI层,将每个特征embedding进行两两做元素积, BI层的输出是一个 k维向量(隐向量的大小),BI层负责了二阶特征组合
可以将FM看成是NFM模型 Hidden Layer层数为0的一种特殊情况

DeepCTR工具
- https://github.com/shenweichen/DeepCTR
- 实现了多种CTR深度模型
- 与Tensorflow 1.4和2.0兼容

数据集:MovieLens_Sample
包括了多个特征:user_id, movie_id, rating, timestamp, title, genres, gender, age, occupation, zip
使用DeepFM、DeepCTR中的WDL、DeepCTR中的NFM,计算RMSE值
data = pd.read_csv("movielens_sample.txt") sparse_features = ["movie_id", "user_id", "gender", "age", "occupation", "zip"] target = ['rating'] …… train, test = train_test_split(data, test_size=0.2) train_model_input = {name:train[name].values for name in feature_names} test_model_input = {name:test[name].values for name in feature_names} # 使用DeepFM进行训练 model = DeepFM(linear_feature_columns, dnn_feature_columns, task='regression') model.compile("adam", "mse", metrics=['mse'], ) history = model.fit(train_model_input, train[target].values,batch_size=256, epochs=1, verbose=True, validation_split=0.2, ) # 使用DeepFM进行预测 pred_ans = model.predict(test_model_input, batch_size=256) # 使用WDL进行训练 model = WDL(linear_feature_columns, dnn_feature_columns, task='regression') model.compile("adam", "mse", metrics=['mse'], ) history = model.fit(train_model_input, train[target].values,batch_size=256, epochs=10, verbose=True, validation_split=0.2, ) # 使用WDL进行预测 pred_ans = model.predict(test_model_input, batch_size=256) # 使用NFM进行训练 model = NFM(linear_feature_columns, dnn_feature_columns, task='regression') model.compile("adam", "mse", metrics=['mse'], ) history = model.fit(train_model_input, train[target].values,batch_size=256, epochs=10, verbose=True, validation_split=0.2, ) # 使用NFM进行预测 pred_ans = model.predict(test_model_input, batch_size=256)
Summary
FM算法的作用:
- 泛化能力强,解决大规模稀疏数据下的特征组合问题,不仅是UserID, ItemID特征
- MF是FM的特例,使用了特征embedding(User,Item)。FM使用了更多Side Information作为特征,同时在进行二阶特征组合权重预估的时候,使用到了MF
- 计算复杂度,可以在线性时间对样本做出预测,通过公式变换将计算复杂度降到O(k*n)
特征组合的作用:
- 更好的模拟真实世界中的影响因素
- DeepFM采用了FM+DNN的方式,在低阶和高阶特征组合上更接近真实世界,因此效果也更好
- 很多特征,在高阶情况下,人很难理解,但是机器可以发现规律(使用DNN模型)


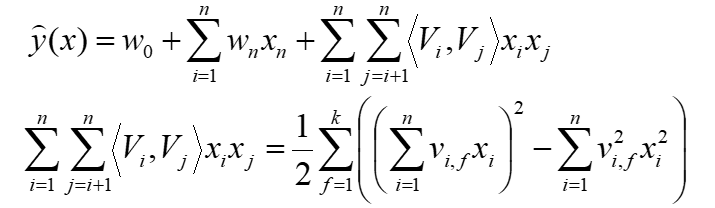
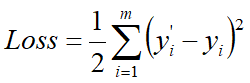
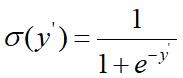

 浙公网安备 33010602011771号
浙公网安备 33010602011771号