Fork me on GitHub

深度学习| 神经网络初步

 

输入input，特征提取（feature representation (hand-crafted)），学习算法（learn algorithm，eg.. SVM）

线性分类器

线性分类器比如逻辑回归、线性SVM，我们会拿到一个决策边界（直线、平面等）；

监督学习很重要的两点：假设函数（从x怎么得到y的）和 损失函数loss function（和标准答案之间差异的函数），

 

 从D维到K维的转换，D维度 * 变换的矩阵(D*K) = K维矩阵  

线性分类器得分函数 

图像数据（32 * 32 * 3的输入矩阵 RGB的像素点）——图像数据 权重/参数f(x, W) ——>  CIFAR-10中的10个类别的得分向量

 f(x, W) = Wx ， （10*1  = 10* 3072   x   3072*1），其中W叫做参数或者权重，b为偏置项，f(x, W) 叫做假设函数x -> y映射关系的函数； 

（3*1  = 3* 4   x   4*1），得到一组得分，即假设函数完成了，dog score的得分最高，但实际它就是一只猫，显然是一组很糟糕的W，我们需要去调整它；

假设函数（计算出得分）、 损失函数（与标准答案的差异）  、损失函数2（交叉熵损失 softmax分类器）

损失函数也叫代价函数/cost function 、客观度/objective 

衡量和标准答案差异的函数

  • 给定w，可以由像素映射到类目得分；
  • 可以调整参数/ 权重W，使得映射的结果和实际类别吻合；
  • 损失函数是用来衡量吻合度的；

损失函数1：hinge loss / 支持向量机损失

  • 对于训练集中的第i张图片数据xi 是一个向量； 
  • 在W下会有一个得分结果向量f(xi, W) 是一个向量；
  • 第j类的得分为我们记作f(xi, W)j 是一个标量scalar； 
  • 则在该样本上的损失我们由下列公式计算得到；

 

假设我们现在有三个类别，而得分函数计算某张图片的得分为f(xi, W) = [13, -7, 11]，而实际的结果是第一类(yi = 0)；

假设△ = 10，上面的公式把错误类别(j != yi) 都遍历了一遍，求值加和： Li = max(0, -7 -13 + 10) + max(0, 11 - 13 + 10)

 因为是线性模型，因此可以简化成：

在这个分类中会有一个正确类比的得分score for correct class，正确得分要比其他分类要高，所以它有一个缓冲带，类比SVM中的缓冲带-街宽 delta ；

如果别的分类在安全警戒线delta之外就不加任何的损失，如果越过了安全警戒线，越过多少就给你加多少惩罚，加到loss里，请回到安全警戒线之外；

j != yi ，遍历一遍非正确的类别，画到数轴上看看离安全警戒线有多近， 越过安全警戒线了，它就是个正值，取大于0的那个值；如果在安全警戒线之外那就是0；第一个是指Σ 是对所有的样本；

所有的样本都会去计算这样一个损失把它加到一块；为了防止过拟合过如正则项；

 

 

 线性分类器得分函数

得到得分函数去评估它的损失函数是唯一方案吗，显然不是的，得到三个得分，无非是想把猫的得分越大越好，另外2类越小越好；

hinge loss的做法是去看看分值之间的绝对差同时设定一个安全警戒线；

另外一种这三个归一化为一个概率向量P，得分不一定是正的也有可能是负的（负数是不能算作概率的）所以不能这么算：Σ(xi/Σxi) = 1 ；

那么加个exi / Σexi ，绝对值保证不了单调性，e的指数次方可以保证单调性；这时我们的得分函数是0~1之间的，加一块等于1；

损失函数2：交叉熵损失（softmax分类器）

逻辑回归LR中的logloss是交叉熵损失的特殊形态，2元的特殊形态；那么它的损失函数是如何得来的呢？

我们得到三个概率向量P1、P、P3，我们希望正确分类P为1，另外两个是0；ΣPi=1，我们希望P越大越好，越大越接近于标准答案1，logP越大越好，-logP越小越好；

损失函数Li越小越好，越小说明和正确答案的差异越小； 

  • 对于训练集中的第i 张图片数据xi ；
  • 在W下会有一个得分结果向量fyi ；
  • 则损失函数记作：

 

2种损失函数的理解

一种办法是基于得分的绝对值，正确类别和其他非正确类别的距离，会加一条安全警戒线，基于安全警戒线去计算一个hinge loss；

另外一种办法是基于概率角度去考虑，e的指数次方这样一个单调函数，拿到一个概率得分向量，概率向量和标准答案去计算一个交叉熵损失cross-entropy loss；

这两种损失函数的差别

hingo loss，只要这个类别在安全警戒线之外，loss就等于0，它就满足了；

cross-entropy loss，logP 越大越接近于1，但它永远也到不了1，-logP即它永远也到不了0这个位置， 它是永远不满足的；

 交叉熵是衡量概率分布之间差异的定义；最大熵是一个模型；

通用的学习框架

深度学习是一个通用的学习框架

 

神经网络

一般神经网络的结构

输入、输出和中间的隐层hidden layer；小圈圈叫神经元，神经元之间的线表示权重值；

 

从逻辑回归到神经元“感知器”

逻辑回归用神经元感知器去表示是如下的形态

两个输入x1、x2和一个偏置项1，加权θ1、θ2，得到一个z，过一个压缩函数g(z)，得到结果a 

 

添加少量隐层 => 浅层神经网络 SNN

在神经元的基础上去构建一个神经网络，一层的隐层或少量的隐层就是SNN，浅层Shallow 神经网络；

 

 

增多中间层  => 深度神经网络（DNN）

 增加多层隐层，即deep 深度神经网络 DNN

 

 神经网络非线性切分

http://playground.tensorflow.org/

神经网络通过输入和中间隐层的计算能够去完成样本点的分类

 

1. 感知器与逻辑门 

神经元完成【逻辑与】and

用神经网络去完成逻辑运算，LR neure，有两个输入x1和x2，输出会过一个g(z)这样子一个函数；

g(z) = g(-30+20*X1+ 20*X2) ，sigmoid函数，X1、X2的值如下得到hθ ；0,0得到-30，无相接近与0即为0；

只有当你两个输入全部为1时才会拿到结果1，即逻辑与的操作；

 

 线性分类器通过与操作去结合的话，就可以拿到一个非线性的切分方式；

 

 

 

神经元完成【逻辑或】or 

g(-10+20*X1+20*X2)，通过sigmoid函数，两个0得到0，含一个1就得到1，逻辑或的操作；

 

2. 强大的空间非线性切分能力

对线性分类器的AND 和OR的组合

完美对平面样本点分布进行分类

 

 如果没有隐层，它就是一个感知器 perception 一条线性的分类边界

 

 

3. 神经网络表达力与过拟合

理论上说单隐层神经网络可以逼近任何连续函数（只要隐层的神经元个数足够多）；（若干个线性分类器去堆叠为一个复杂的曲线）

虽然从数学上表达能力一致，但是很多隐藏层的神经网络比单隐藏层的神经网络工程效果好很多；

对于一些分类数据（比如CTR预估里），3层神经网络效果优于2层神经网络，但是如果把层数再不断增加（4,5,6层），对最后结果的帮助就没有那么大的跳变了；

图像数据比较特殊，是一种深层（多层次）的结构化数据，深层次的卷积神经网络，能够更充分和准确地把这些层级信息表达出来；

 

  • 提升隐层层数或者隐层神经元个数，神经网络“容量”会变大，空间表达力会变强；
  • 过多的隐层和神经元节点，会带来过拟合问题；
  • 不要试图通过降低神经网络参数量来减缓过拟合，用正则化或者dropout；

 

 

4. BP算法与SGD 

神经网络结构

输入Xn、输出Om ，中间若干的隐层，Wx + b（基于上层的组合运算得到一个解），会接一个激活函数activation function 非线性变换；

如果不加非线性变换，它加再多的线性变换都是线性的；

 

传递函数

数学特性比较好的函数

sigmoid中心对称，它的导数为g (z)' = g(z) * (1-g(z)) 

 

 BP算法（反向传播）

  • “正向传播”求损失，“反向传播”回传误差；
  • 根据误差信号修正每层的权重；

 

  •  BP算法也叫δ算法；
  • 以3层的感知器为例

损失函数E，loss function  mse，假设这里不是分类是一个回归的问题，输出结果O、标准结果d，0到l个输出结果；

f为激活函数/传递函数如sigmoid，netk , netk是前一层算出来的；

反向传播在求导数时，它不是可以直接求的，它是有几层的变换是一个复合函数，必须得沿着神经网络从最后一层往前推，把每一层的导数都求出来做一个乘法，它就是一个求导的链式法则；

 

SGD 

误差E有了，怎么调整权重让误差不断减小？梯度下降（严格意义上说是沿着负梯度的方向去更新W，梯度是一个上升的方向）

E是权重W的函数，我们需要找到使得函数值最小的W；

BP算法例子

有两个输入0.5和0.1，两个输出0.1和0.99，想做一个回归；一个偏置项是0.35，另外一个偏置项是0.6；权重W1...W8，有一个隐层

 前向（前馈）运算

与标准答案之间差异是多少（o-d）2

求出neth1 ，需要过一个sigmoid函数；

从第一层如何到第二层，求neto1，代到sigmoid中得到outo1 ，最终得到Etotal 损失loss；

 

反向传播 

拿到损失函数后，求偏导；∂L / ∂w5 ；复合函数求导；

 

 

反向传播与参数更新

 

 

 

神经网络示例

tensorflow与多层感知器完成样本分类

 

 手写神经网络怎么对样本点做非线性切分

## 人工神经网络初步

人工神经网络其实在很久以前就被提出来了，苦于当时没有足够强大的硬件(比如现在铺天盖地的GPU)去支撑理论的实践，数据的支撑也不够，因此消停了非常长的时间。<br><br>
当然，它的热度在近两年被推到了一个近乎极端的状态，似乎是个好点的实验室，是个大型点的互联网公司，不说自己会点深度学习和神经网络都不好意思说自己是这个圈子里混的。当然，媒体的炒作是一方面啦，但是神经网络确实在近期的一些任务中表现出了非常强势的优势。<br><br>
比如在很多分类问题中，样本是不可线性切分的，那特征的处理就尤为重要了，有意思的是，这正是神经网络所擅长的，在每一次的前向计算过程中，就在自动地做feature engineering，而到达softmax层的时候，其实构造出来的feature空间里，样本已经是能近似线性切分的了，于是三下五除二把其他分类器远远甩在后面了。<br><br>
咱们来具体看看，简单的人工神经网络是怎么样对样本点做非线性切分的。
import numpy as np
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
# 手动生成一个随机的平面点分布，并画出来
np.random.seed(0)
X, y = make_moons(200, noise=0.20)
plt.scatter(X[:,0], X[:,1], s=40, c=y, cmap=plt.cm.Spectral)
plt.show()
画出了这样一幅图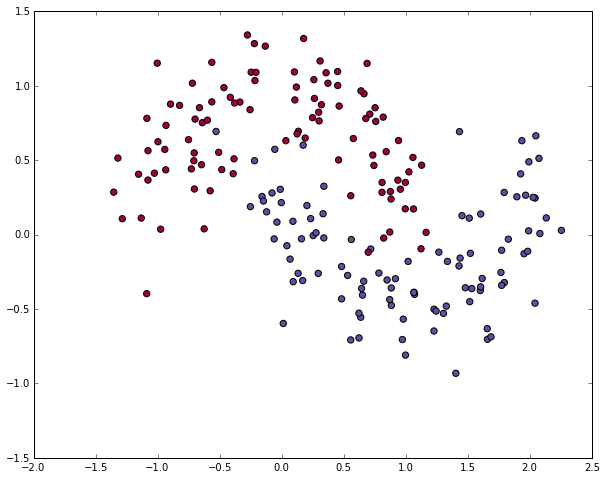
![](http://d3kbpzbmcynnmx.cloudfront.net/wp-content/uploads/2015/09/nn-from-scratch-dataset.png)
### 咱们定义一个函数用来画我们分类结果的决策边界（也就是分界线）
# 咱们先顶一个一个函数来画决策边界
def plot_decision_boundary(pred_func):

    # 设定最大最小值，附加一点点边缘填充
    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    h = 0.01

    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

    # 用预测函数预测一下
    Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    # 然后画出图
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral)
### 我们先用传统的逻辑回归来做一下分类，并画出判定边界
from sklearn.linear_model import LogisticRegressionCV
#咱们先来瞄一眼逻辑斯特回归对于它的分类效果
clf = LogisticRegressionCV()
clf.fit(X, y)
 
# 画一下决策边界
plot_decision_boundary(lambda x: clf.predict(x))
plt.title("Logistic Regression")
plt.show()
咱们看到下面这样的结果<br>
很好理解对吧，因为线性切分，决策边界是直线，这条直线只能尽量让某一类点落在某一侧，但是永远做不到真的完全切分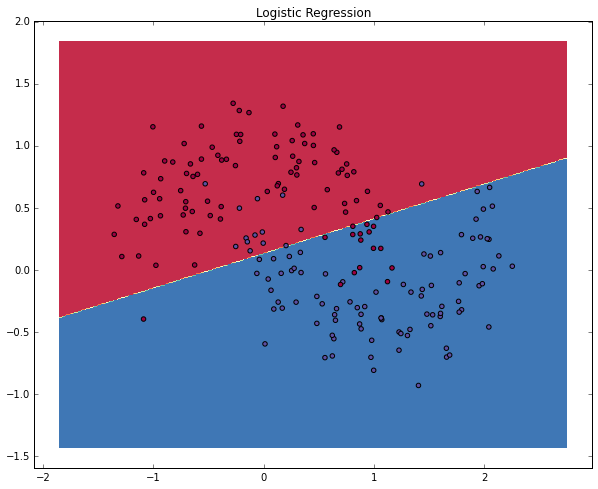
![](http://d3kbpzbmcynnmx.cloudfront.net/wp-content/uploads/2015/09/nn-from-scratch-lr-decision-boundary.png)
## 咱们来试一个简单的人工神经网络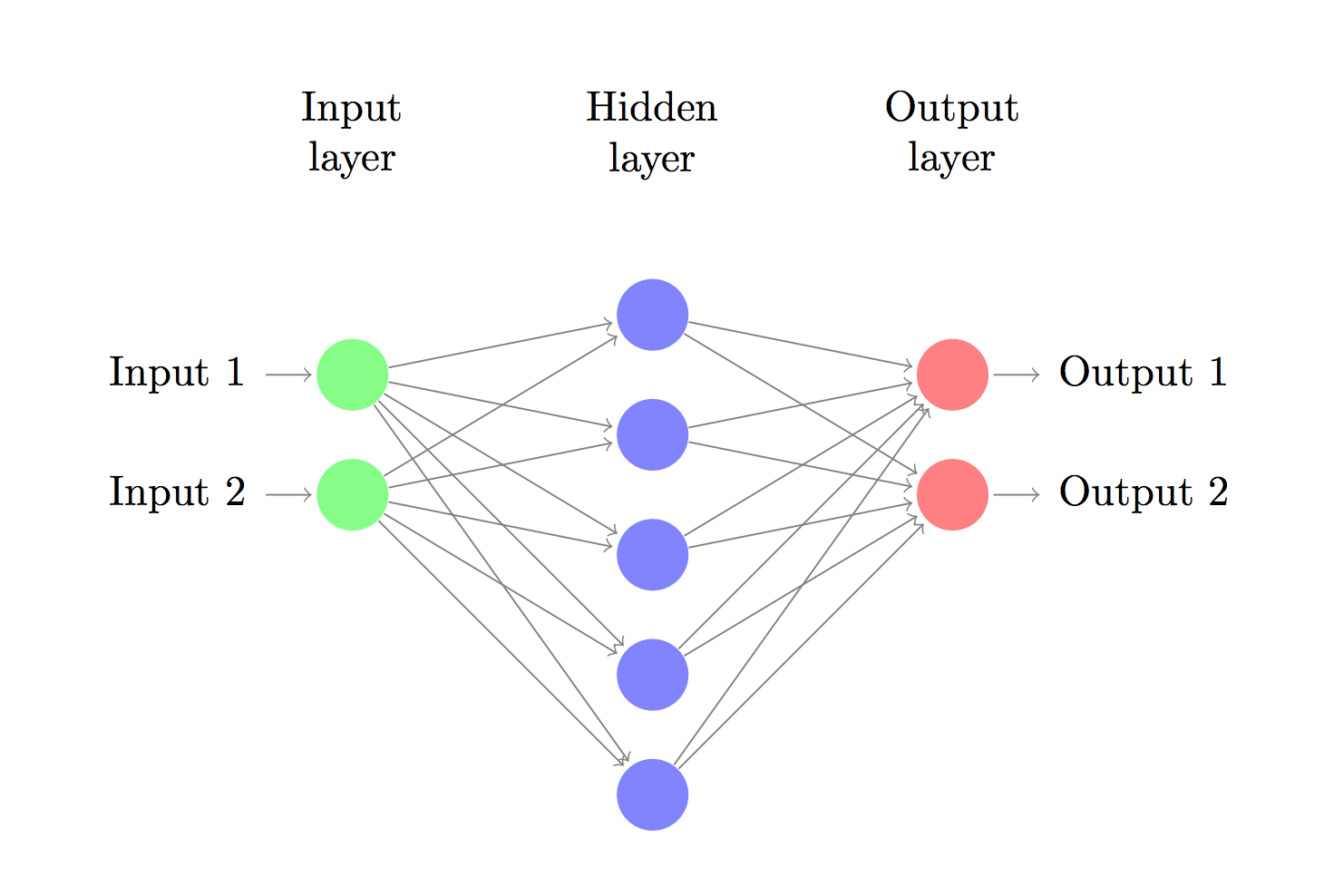
![](http://www.wildml.com/wp-content/uploads/2015/09/nn-from-scratch-3-layer-network.png)
![](http://s0.wp.com/latex.php?zoom=2&latex=%5Cbegin%7Baligned%7D++z_1+%26+%3D+xW_1+%2B+b_1+%5C%5C++a_1+%26+%3D+%5Ctanh%28z_1%29+%5C%5C++z_2+%26+%3D+a_1W_2+%2B+b_2+%5C%5C++a_2+%26+%3D+%5Chat%7By%7D+%3D+%5Cmathrm%7Bsoftmax%7D%28z_2%29++%5Cend%7Baligned%7D&bg=ffffff&fg=000&s=0)
![](http://s0.wp.com/latex.php?zoom=2&latex=W_1+%5Cin+%5Cmathbb%7BR%7D%5E%7B2%5Ctimes500%7D&bg=ffffff&fg=000&s=0)
![](http://s0.wp.com/latex.php?zoom=2&latex=b_1+%5Cin+%5Cmathbb%7BR%7D%5E%7B500%7D&bg=ffffff&fg=000&s=0)
![](http://s0.wp.com/latex.php?zoom=2&latex=W_2+%5Cin+%5Cmathbb%7BR%7D%5E%7B500%5Ctimes2%7D&bg=ffffff&fg=000&s=0)
![](http://s0.wp.com/latex.php?zoom=2&latex=b_2+%5Cin+%5Cmathbb%7BR%7D%5E%7B2%7D&bg=ffffff&fg=000&s=0)
## 这是一个分类问题，因此我们用softmax分类器，并且用交叉熵损失作为损失函数
![](http://s0.wp.com/latex.php?zoom=2&latex=%5Cbegin%7Baligned%7D++L%28y%2C%5Chat%7By%7D%29+%3D+-+%5Cfrac%7B1%7D%7BN%7D+%5Csum_%7Bn+%5Cin+N%7D+%5Csum_%7Bi+%5Cin+C%7D+y_%7Bn%2Ci%7D+%5Clog%5Chat%7By%7D_%7Bn%2Ci%7D++%5Cend%7Baligned%7D++&bg=ffffff&fg=000&s=0)
## BP计算梯度以便使用(随机)梯度下降
![](http://s0.wp.com/latex.php?zoom=2&latex=%5Cbegin%7Baligned%7D++%26+%5Cdelta_3+%3D+%5Chat%7By%7D+-+y+%5C%5C++%26+%5Cdelta_2+%3D+%281+-+%5Ctanh%5E2+z_1%29+%5Ccirc+%5Cdelta_3W_2%5ET+%5C%5C++%26+%5Cfrac%7B%5Cpartial%7BL%7D%7D%7B%5Cpartial%7BW_2%7D%7D+%3D+a_1%5ET+%5Cdelta_3+%5C%5C++%26+%5Cfrac%7B%5Cpartial%7BL%7D%7D%7B%5Cpartial%7Bb_2%7D%7D+%3D+%5Cdelta_3%5C%5C++%26+%5Cfrac%7B%5Cpartial%7BL%7D%7D%7B%5Cpartial%7BW_1%7D%7D+%3D+x%5ET+%5Cdelta2%5C%5C++%26+%5Cfrac%7B%5Cpartial%7BL%7D%7D%7B%5Cpartial%7Bb_1%7D%7D+%3D+%5Cdelta2+%5C%5C++%5Cend%7Baligned%7D++&bg=ffffff&fg=000&s=0)
num_examples = len(X) # 样本数
nn_input_dim = 2 # 输入的维度
nn_output_dim = 2 # 输出的类别个数
 
# 梯度下降参数
epsilon = 0.01 # 学习率
reg_lambda = 0.01 # 正则化参数

# 定义损失函数(才能用梯度下降啊...)
def calculate_loss(model):
    W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']
    # 向前推进，前向运算
    z1 = X.dot(W1) + b1
    a1 = np.tanh(z1)
    z2 = a1.dot(W2) + b2
    exp_scores = np.exp(z2)
    probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
    # 计算损失
    corect_logprobs = -np.log(probs[range(num_examples), y])
    data_loss = np.sum(corect_logprobs)
    # 也得加一下正则化项
    data_loss += reg_lambda/2 * (np.sum(np.square(W1)) + np.sum(np.square(W2)))
    return 1./num_examples * data_loss
# 完整的训练建模函数定义
def build_model(nn_hdim, num_passes=20000, print_loss=False):
    '''
    参数：
    1) nn_hdim: 隐层节点个数
    2）num_passes: 梯度下降迭代次数
    3）print_loss: 设定为True的话，每1000次迭代输出一次loss的当前值
    '''
    # 随机初始化一下权重呗
    np.random.seed(0)
    W1 = np.random.randn(nn_input_dim, nn_hdim) / np.sqrt(nn_input_dim)
    b1 = np.zeros((1, nn_hdim))
    W2 = np.random.randn(nn_hdim, nn_output_dim) / np.sqrt(nn_hdim)
    b2 = np.zeros((1, nn_output_dim))
 
    # 这是咱们最后学到的模型
    model = {}
     
    # 开始梯度下降...
    for i in xrange(0, num_passes):
 
        # 前向运算计算loss
        z1 = X.dot(W1) + b1
        a1 = np.tanh(z1)
        z2 = a1.dot(W2) + b2
        exp_scores = np.exp(z2)
        probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
 
        # 反向传播
        delta3 = probs
        delta3[range(num_examples), y] -= 1
        dW2 = (a1.T).dot(delta3)
        db2 = np.sum(delta3, axis=0, keepdims=True)
        delta2 = delta3.dot(W2.T) * (1 - np.power(a1, 2))
        dW1 = np.dot(X.T, delta2)
        db1 = np.sum(delta2, axis=0)
 
        # 加上正则化项
        dW2 += reg_lambda * W2
        dW1 += reg_lambda * W1
 
        # 梯度下降更新参数
        W1 += -epsilon * dW1
        b1 += -epsilon * db1
        W2 += -epsilon * dW2
        b2 += -epsilon * db2
         
        # 得到的模型实际上就是这些权重
        model = { 'W1': W1, 'b1': b1, 'W2': W2, 'b2': b2}
         
        # 如果设定print_loss了，那我们汇报一下中间状况
        if print_loss and i % 1000 == 0:
          print "Loss after iteration %i: %f" %(i, calculate_loss(model))
     
    return model
# 判定结果的函数
def predict(model, x):
    W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']
    # 前向运算
    z1 = x.dot(W1) + b1
    a1 = np.tanh(z1)
    z2 = a1.dot(W2) + b2
    exp_scores = np.exp(z2)
    # 计算概率输出最大概率对应的类别
    probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
    return np.argmax(probs, axis=1)
# 建立隐层有3个节点(神经元)的神经网络
model = build_model(3, print_loss=True)
 
# 然后再把决策/判定边界画出来
plot_decision_boundary(lambda x: predict(model, x))
plt.title("Decision Boundary for hidden layer size 3")
plt.show()
### 咱们看到这样一个图，隐层有3个节点的神经网络能够区分得还不错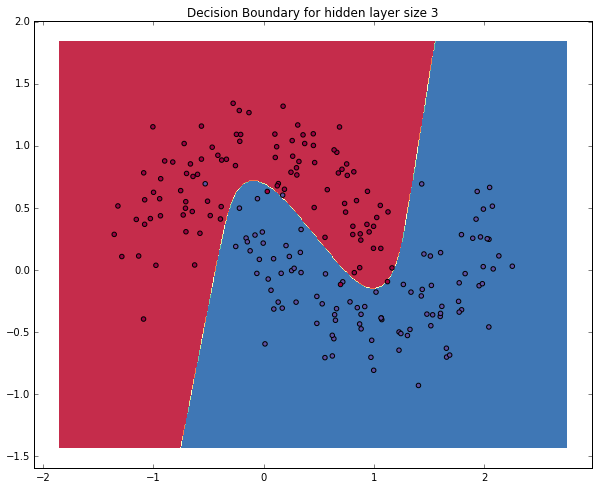
![](http://d3kbpzbmcynnmx.cloudfront.net/wp-content/uploads/2015/09/nn-from-scratch-h3.png)
# 然后听闻你想知道不同的隐层节点个数对结果的影响？
# 那咱们来一起看看吧
plt.figure(figsize=(16, 32))
# 设定不同的隐层节点(神经元)个数
hidden_layer_dimensions = [1, 2, 3, 4, 5, 20, 50]
for i, nn_hdim in enumerate(hidden_layer_dimensions):
    plt.subplot(5, 2, i+1)
    plt.title('Hidden Layer size %d' % nn_hdim)
    model = build_model(nn_hdim)
    plot_decision_boundary(lambda x: predict(model, x))
plt.show()
### 结果差不多是这个样子的
![](http://d3kbpzbmcynnmx.cloudfront.net/wp-content/uploads/2015/09/nn-from-scratch-hidden-layer-varying.png)

google wide & deep model

# coding: utf-8
'''
用keras2.x写的google Wide&&Deep model
'''
import pandas as pd
from keras import Input, Model
from keras.layers import Dense, Concatenate
from sklearn.preprocessing import MinMaxScaler

# 所有的数据列
COLUMNS = [
    "age", "workclass", "fnlwgt", "education", "education_num", "marital_status",
    "occupation", "relationship", "race", "gender", "capital_gain", "capital_loss",
    "hours_per_week", "native_country", "income_bracket"
]

# 标签列
LABEL_COLUMN = "label"

# 类别型特征变量
CATEGORICAL_COLUMNS = [
    "workclass", "education", "marital_status", "occupation", "relationship",
    "race", "gender", "native_country"
]

# 连续值特征变量
CONTINUOUS_COLUMNS = [
    "age", "education_num", "capital_gain", "capital_loss", "hours_per_week"
]


# 加载文件
def load(filename):
    with open(filename, 'r') as f:
        skiprows = 1 if 'test' in filename else 0
        df = pd.read_csv(
            f, names=COLUMNS, skipinitialspace=True, skiprows=skiprows, engine='python'
        )
        # 缺省值处理
        df = df.dropna(how='any', axis=0)
    return df


# 预处理
def preprocess(df):
    df[LABEL_COLUMN] = df['income_bracket'].apply(lambda x: ">50K" in x).astype(int)
    df.pop("income_bracket")
    y = df[LABEL_COLUMN].values
    df.pop(LABEL_COLUMN)

    df = pd.get_dummies(df, columns=[x for x in CATEGORICAL_COLUMNS])

    # TODO: 对特征进行选择，使得网络更高效

    # TODO: 特征工程，比如加入交叉与组合特征

    df = pd.DataFrame(MinMaxScaler().fit_transform(df), columns=df.columns)

    X = df.values
    return X, y


def main():
    df_train = load('adult.data')
    df_test = load('adult.test')
    df = pd.concat([df_train, df_test])
    train_len = len(df_train)

    X, y = preprocess(df)
    X_train = X[:train_len]
    y_train = y[:train_len]
    X_test = X[train_len:]
    y_test = y[train_len:]
    input_layer = Input(shape=(X_train.shape[1]))
    wide_layer = Dense(1, activation='sigmoid')(input_layer)
    deep_layer = Dense(64, activation='relu')(input_layer)
    deep_layer = Dense(32, activation='relu')(deep_layer)
    deep_layer = Dense(16, activation='relu')(deep_layer)

    wide_deep_layer = Concatenate(axis=1)([wide_layer, deep_layer])

    output_layer = Dense(1, activation='sigmoid')(wide_deep_layer)

    model = Model(inputs=input_layer, outputs=output_layer)

    model.compile(
        optimizer='rmsprop',
        loss='binary_crossentropy',
        metrics=['accuracy']
    )

    # 模型训练
    model.fit(X_train, y_train, epochs=10, batch_size=32, validation_data=(X_test, y_test))

    # loss与准确率评估
    loss, accuracy = model.evaluate(X_test, y_test)
    print('\n', 'test loss:', loss)
    print('\n', 'test accuracy:', accuracy)


if __name__ == '__main__':
    main()

输出如下：

Epoch 1/10
1018/1018 [==============================] - 2s 2ms/step - loss: 0.3593 - accuracy: 0.8315 - val_loss: 0.3369 - val_accuracy: 0.8422
Epoch 2/10
1018/1018 [==============================] - 1s 1ms/step - loss: 0.3333 - accuracy: 0.8454 - val_loss: 0.3424 - val_accuracy: 0.8429
Epoch 3/10
1018/1018 [==============================] - 1s 1ms/step - loss: 0.3264 - accuracy: 0.8487 - val_loss: 0.3239 - val_accuracy: 0.8490
Epoch 4/10
1018/1018 [==============================] - 1s 1ms/step - loss: 0.3232 - accuracy: 0.8507 - val_loss: 0.3222 - val_accuracy: 0.8514
Epoch 5/10
1018/1018 [==============================] - 1s 1ms/step - loss: 0.3203 - accuracy: 0.8513 - val_loss: 0.3228 - val_accuracy: 0.8487
Epoch 6/10
1018/1018 [==============================] - 1s 1ms/step - loss: 0.3170 - accuracy: 0.8535 - val_loss: 0.3186 - val_accuracy: 0.8509
Epoch 7/10
1018/1018 [==============================] - 1s 1ms/step - loss: 0.3154 - accuracy: 0.8544 - val_loss: 0.3169 - val_accuracy: 0.8523
Epoch 8/10
1018/1018 [==============================] - 1s 1ms/step - loss: 0.3133 - accuracy: 0.8568 - val_loss: 0.3176 - val_accuracy: 0.8523
Epoch 9/10
1018/1018 [==============================] - 1s 1ms/step - loss: 0.3112 - accuracy: 0.8582 - val_loss: 0.3192 - val_accuracy: 0.8533
Epoch 10/10
1018/1018 [==============================] - 1s 1ms/step - loss: 0.3103 - accuracy: 0.8579 - val_loss: 0.3162 - val_accuracy: 0.8541
509/509 [==============================] - 0s 786us/step - loss: 0.3162 - accuracy: 0.8541

 test loss: 0.316202849149704

 test accuracy: 0.8540630340576172

Process finished with exit code 0

 

 
 
posted @ 2023-03-30 07:49  kris12  阅读(134)  评论(0)  编辑  收藏  举报
levels of contents