算法| 高级动态规划

 

动态规划 Dynamic Programming

1. “Simplifying a complicated problem by breaking it down into simpler sub-problems”
　　(in a recursive manner)

2. Divide & Conquer + Optimal substructure
　　分治 + 最优子结构

3. 顺推形式： 动态递推

 

DP 顺推模板
    function DP():
        dp = [][] # ⼆维情况
        for i = 0 .. M {
            for j = 0 .. N {
                dp[i][j] = _Function(dp[i’][j’]…)
    }
}
return dp[M][N];    

关键点：

动态规划 和 递归或者分治 没有根本上的区别（关键看有无最优的子结构）

拥有共性：找到重复子问题（找到重复性和重复子问题，然后化繁为简，庖丁解牛似的把一个大问题分解成各个重复的子问题）

差异性：最优子结构、中途可以淘汰次优解（动态规划用来处理有所谓中间的重复性以及所谓的最优子结构，在中途可以淘汰次优解）

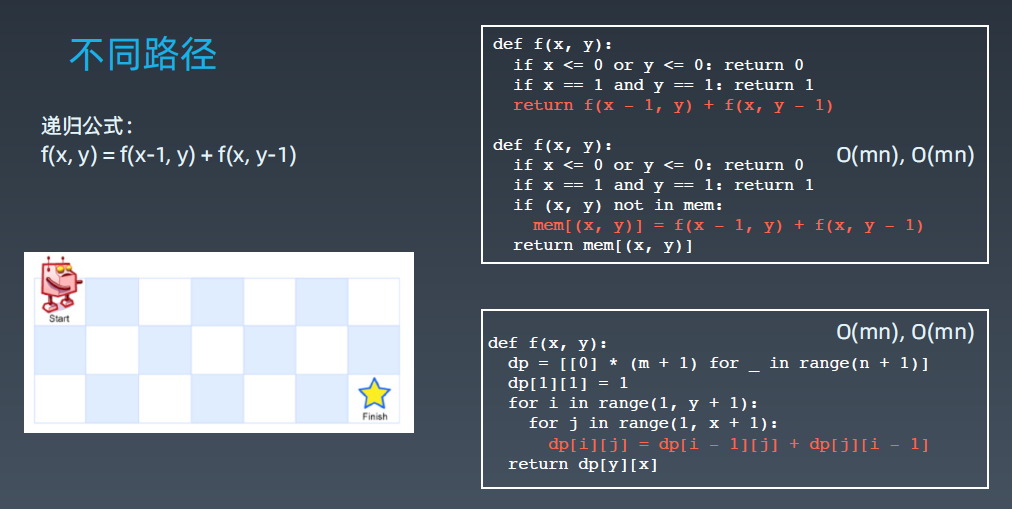
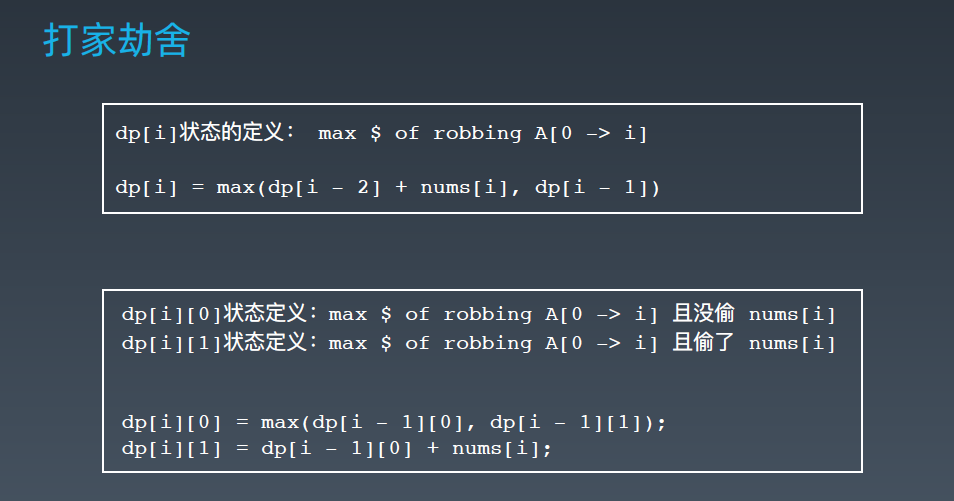
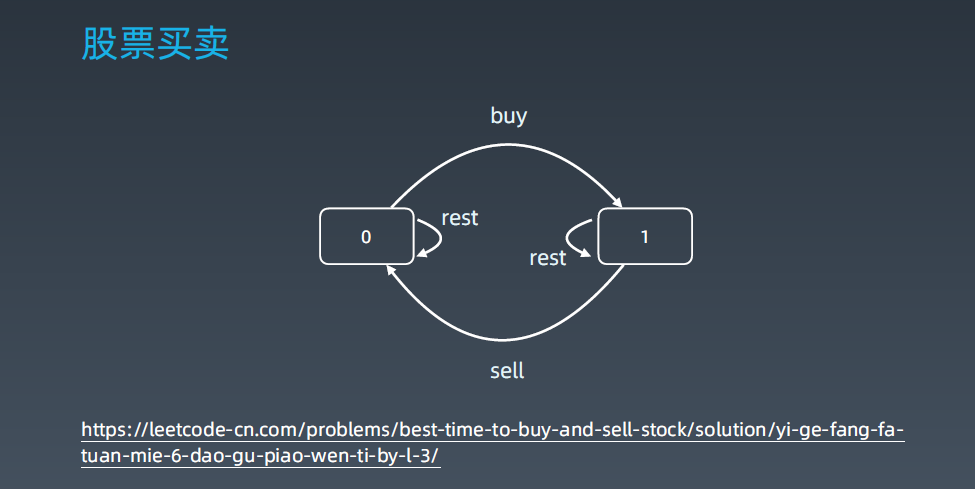
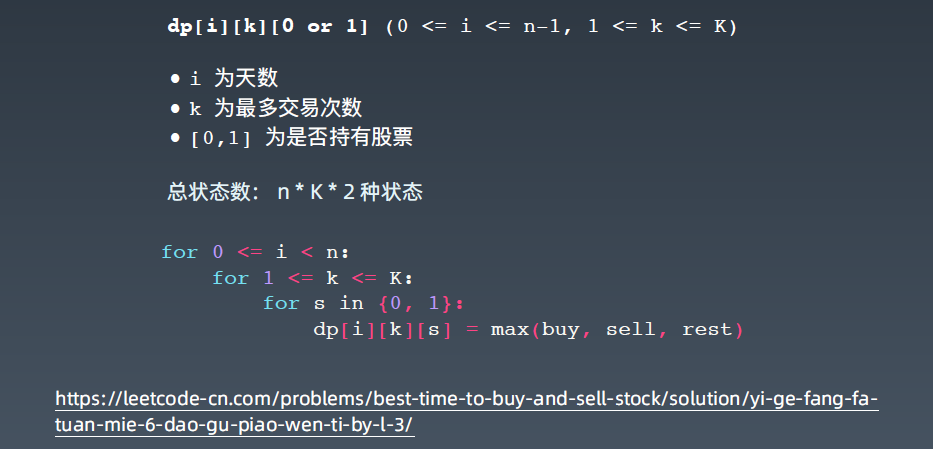
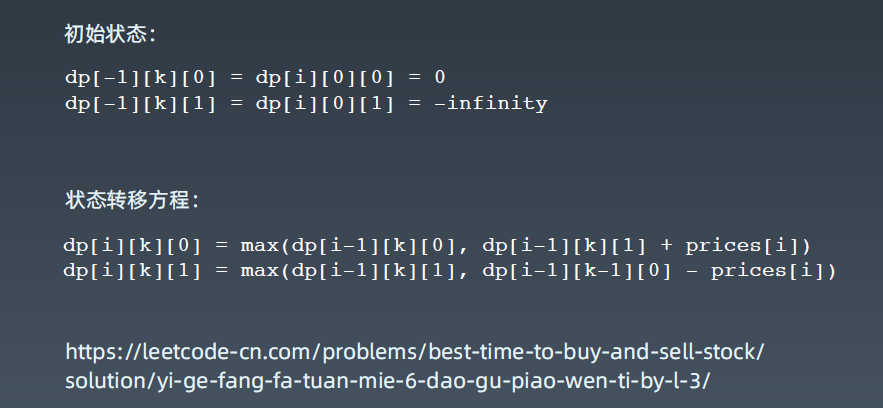
常见的 DP 题目和状态方程

  

 

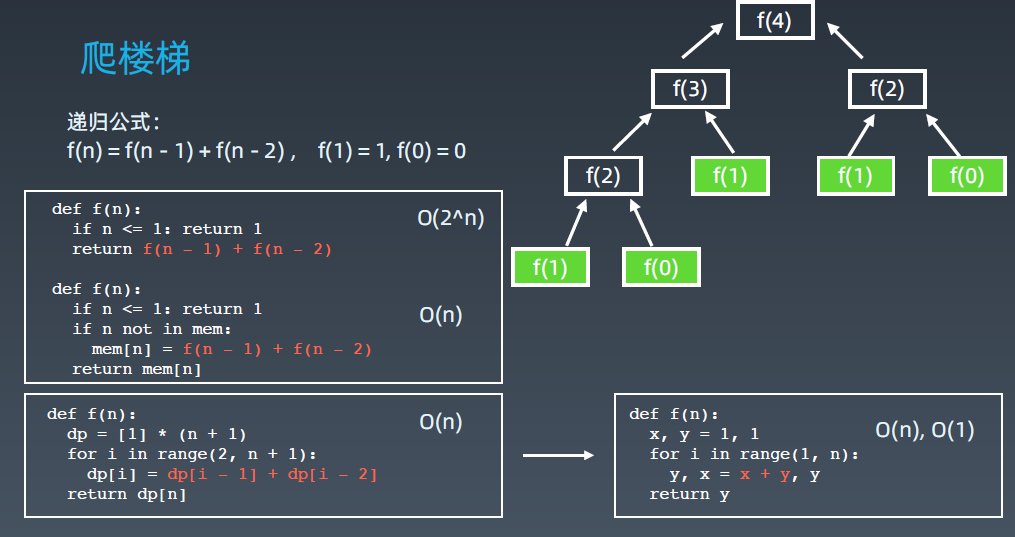
 爬楼梯问题和硬币置换问题，有异曲同工之处