算法-01| Cache缓存淘汰算法
1. Cache缓存
①.记忆
②.钱包-储物柜
③.代码模块
一个经典的链表应用场景，那就是 LRU 缓存淘汰算法。
缓存是一种提高数据读取性能的技术，在硬件设计、软件开发中都有着非常广泛的应用，比如常见的 CPU 缓存、数据库缓存、浏览器缓存等等。
缓存的大小有限，当缓存被用满时，哪些数据应该被清理出去，哪些数据应该被保留？这就需要缓存淘汰策略来决定。
常见的策略有三种：
- 先进先出策略 FIFO（First In，First Out）
- 少使 用策略 LFU（Least Frequently Used）
- 近少使用策略 LRU（Least Recently Used）
打个比方说，你买了很多本技术书，但发现这些书太多，太占书房空间，需要个大扫除，扔掉一些书籍。你会选择扔掉哪些书呢？对应一下，你的选择标准是不是和上面的三种策略神似。
1.1. CPUSocket
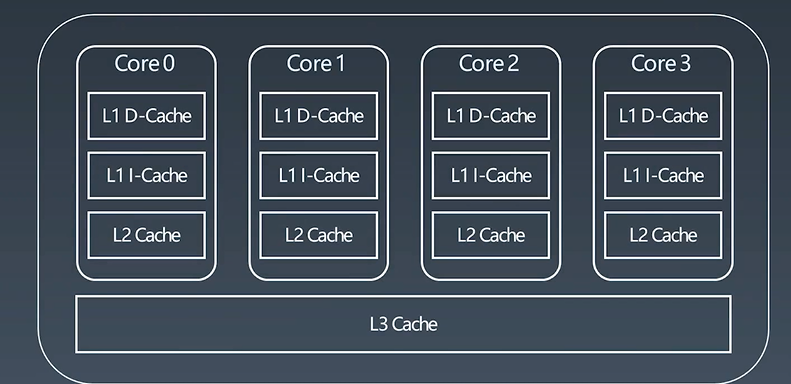
Understanding the Meltdown exploit – in my own simple words
上图为四核CPU，三级缓存（L1 Cache，L2 Cache ，L3 Cache）；
每一个核里边就有L1 D-Cache，L1 l-Cache，L2 Cache，L3 Cache；最常用的数据马上要给CPU的计算模块进行计算处理的就放在L1里边，次之不常用的就放在L1 l-Cache里边，再次之放在L2Cache里边，最后放在L3 Cache里边。外边即内存。他们的速度 L1 D-Cache > L1 l-Cache > L2-Cache > L3-Cache
体积（能存的数据多少）即 L1 D-Cache < L1 l-Cache < L2-Cache < L3-Cache
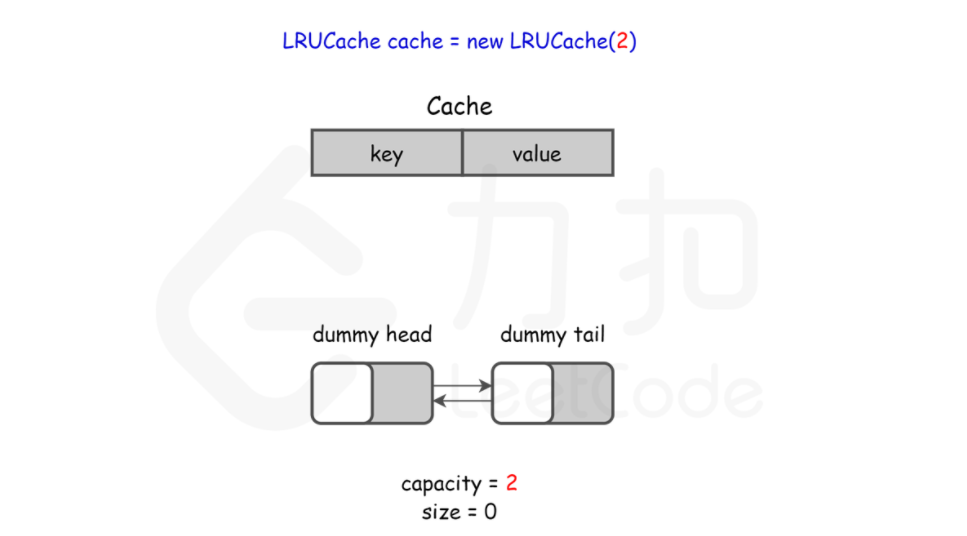
1.2. LRUCache
两个要素：
大小
替换策略（least recent use -- 最近最少使用）
实现机制：
HashTable+DoubleLinkedList
复杂度分析：
O(1)查询
O(1)修改、 更新
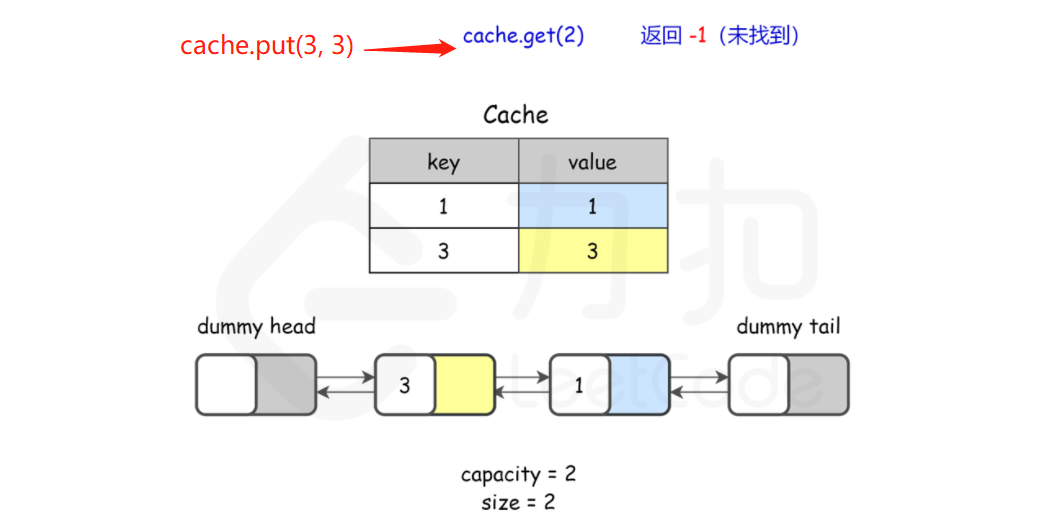
LRU Cache工作示例：
更新原则 least recent use
替换策略:
LFU - least frequently used
LRU - least recently used
如何基于链表实现 LRU 缓存淘汰算法？
维护一个有序单链表，越靠近链表尾部的结点是越早之前访问的。当有一个新的数据被访问时，从链表头开始顺序遍历链表。
①. 如果此数据之前已经被缓存在链表中了，遍历得到这个数据对应的结点，并将其从原来的位置删除，然后再插入到链表的头部。
②. 如果此数据没有在缓存链表中，又可以分为两种情况：
- 如果此时缓存未满，则将此结点直接插入到链表的头部；
- 如果此时缓存已满，则链表尾结点删除，将新的数据结点插入链表的头部。
这样我们就用链表实现了一个 LRU 缓存。
m 缓存访问的时间复杂度是多少。因为不管缓存有没有满，都需要遍历一遍链表，所以这种基于链表的实现思路，缓存访问的时间复杂度为 O(n)。
可以继续优化这个实现思路，比如引入散列表（Hash table）来记录每个数据的位置，将缓存访问的时间复杂度降到 O(1)。
LRUCache Python
class LRUCache(object):
def __init__(self, capacity):
self.dic = collections.OrderedDict()
self.remain = capacity
def get(self, key):
if key not in self.dic:
return -1
v = self.dic.pop(key)
self.dic[key] = v # key as the newest one
return v
def put(self, key, value):
if key in
self.dic: self.dic.pop(key)
else:
if self.remain > 0:
self.remain -= 1
else: # self.dic is full
self.dic.popitem(last=False)
self.dic[key] = value
LRUCache Java
private Map<Integer, Integer> map;
public LRUCache(int capacity) {
map = new LinkedCappedHashMap<>(capacity);
}
public int get(int key) {
if (!map.containsKey(key)) {
return -1;
}
return map.get(key);
}
public void put(int key, int value) {
map.put(key, value);
}
private static class LinkedCappedHashMap<K, V> extends LinkedHashMap<K, V> {
int maximumCapacity;
LinkedCappedHashMap(int maximumCapacity) {
// initialCapacity代表map的容量, loadFactor代表加载因子, accessOrder默认false,如果要按读取顺序排序需要将其设为true
super(16, 0.75f, true);//default initial capacity (16) and load factor (0.75) and accessOrder (false)
this.maximumCapacity = maximumCapacity;
}
/* 重写 removeEldestEntry()函数，就能拥有我们自己的缓存策略 */
protected boolean removeEldestEntry(Map.Entry eldest) {
return size() > maximumCapacity;
}
}
2. 链表+散列表的使用
* 哈希表 + 双向链表
* 时间复杂度：对于 put 和 get 都是 O(1)
* 空间复杂度：O(capacity),因为哈希表和双向链表最多存储 capacity+1 个元素。
* 算法
* LRU 缓存机制可以通过哈希表辅以双向链表实现，我们用一个哈希表和一个双向链表维护所有在缓存中的键值对。
* 双向链表按照被使用的顺序存储了这些键值对，靠近头部的键值对是最近使用的，而靠近尾部的键值对是最久未使用的。
* 哈希表即为普通的哈希映射（HashMap），通过缓存数据的键映射到其在双向链表中的位置。
* 这样以来，我们首先使用哈希表进行定位，找出缓存项在双向链表中的位置，随后将其移动到双向链表的头部，即可在 O(1)的时间内完成 get 或者 put 操作。具体的方法如下：
* 对于 get 操作，首先判断 key 是否存在：
* 如果 key 不存在，则返回 −1；
* 如果 key 存在，则 key 对应的节点是最近被使用的节点。通过哈希表定位到该节点在双向链表中的位置，并将其移动到双向链表的头部，最后返回该节点的值。
* 对于 put 操作，首先判断 key 是否存在：
* 如果 key 不存在，使用 key 和 value 创建一个新的节点，在双向链表的头部添加该节点，并将 key 和该节点添加进哈希表中。然后判断双向链表的节点数是否超出容量，如果超出容量，则删除双向链表的尾部节点，并删除哈希表中对应的项；
* 如果 key 存在，则与 get 操作类似，先通过哈希表定位，再将对应的节点的值更新为 value，并将该节点移到双向链表的头部。
* 上述各项操作中，访问哈希表的时间复杂度为 O(1)，在双向链表的头部添加节点、在双向链表的尾部删除节点的复杂度也为 O(1)。而将一个节点移到双向链表的头部，可以分成「删除该节点」和「在双向链表的头部添加节点」两步操作，都可以在 O(1)时间内完成。
*
* 小贴士
* 在双向链表的实现中，使用一个伪头部（dummy head）和伪尾部（dummy tail）标记界限，这样在添加节点和删除节点的时候就不需要检查相邻的节点是否存在。
