算法 08| 字符串算法| BF| RK
1. 字符串概念
• Python:
x = ‘abbc’ x = “abbc”
• Java:
String x = “abbc”;
Python和Java中的string 都是不可变数据类型， immutable：https://lemire.me/blog/2017/07/07/are-your-stringsimmutable/
当加一个或减一个字符它就新生成一个String，原来的String还是原来的内容。immutable它也是有好处，它是线程安全的，可变有可能在多线程环境里面有一些问题。
• C++:
string x(“abbc”)，mutable，是可变的类型
2. 字符串的遍历
• Python:
for ch in “abbc”: print(ch)
• Java:
String x = “abbc”;
for (int i = 0; i < x.size(); ++i) { char ch = x.charAt(i); } for ch in x.toCharArray() { System.out.println(ch); }
• C++:
string x(“abbc”); for (int i = 0; i < s1.length(); i++) { cout << x[i]; }
3. 字符串比较
Java: String x = “abb”; String y = “abb”; x == y —-> false， java中它是比较它们的指针，比较它们的reference的地址，而不是比较字符串里边的内容，变量x，y是两个不同的变量，它指向内存中的不同地址， x.equals(y) —-> true //比较变量x和y的内容； x.equalsIgnoreCase(y) —-> true //忽略大小写的进行比较。
4. 字符串匹配算法
4.1 BF（Brute Force）算法
BF算法（Brute Force）中文叫作暴力匹配算法，也叫朴素匹配算法 --- 时间复杂度 O(mn)。
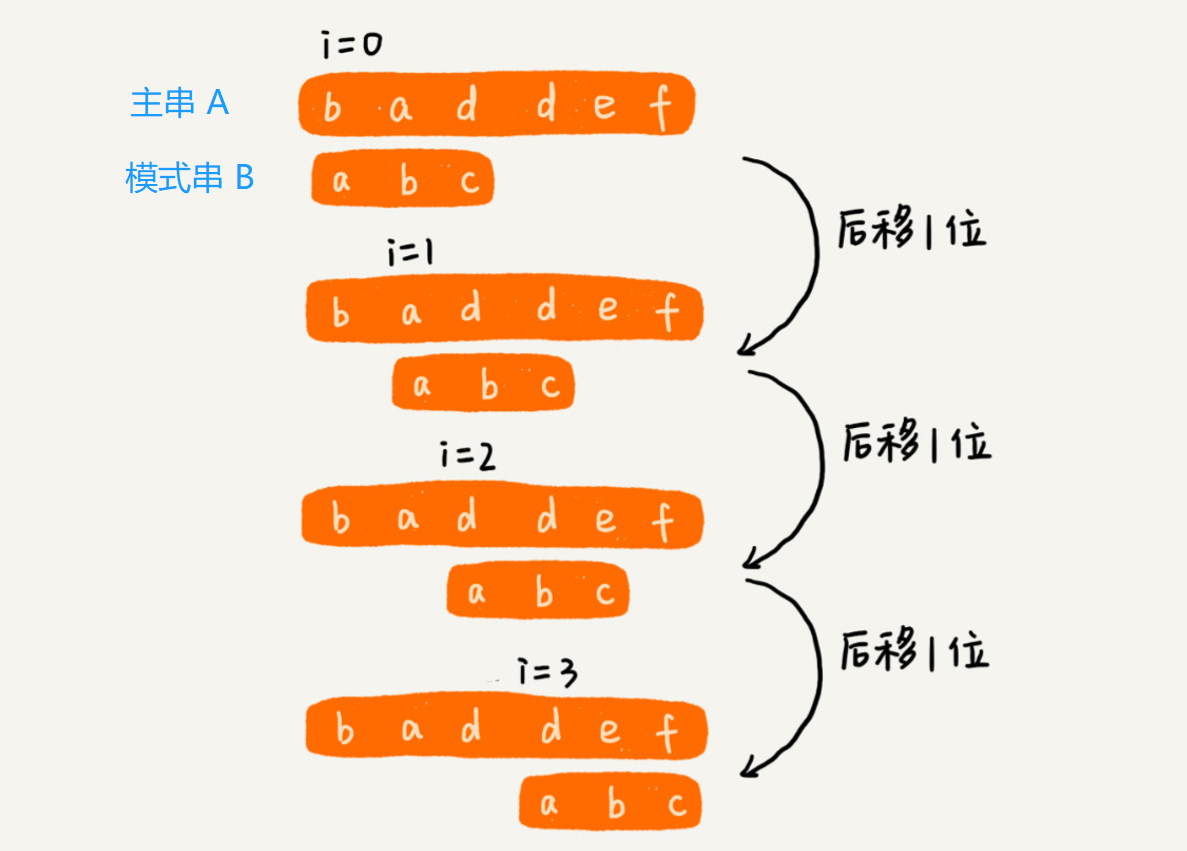
主串和模式串，在字符串 A 中查找字符串 B，那字符串 A 就是主串，字符串 B 就是模式串。把主串的长度记作 n，模式串的长度记作 m。在主串中查找模式串，所以 n>m。
作为最简单、最暴力的字符串匹配算法，BF 算法的思想可以用一句话来概括，那就是，在主串中，检查起始位置分别是 0、1、2…n-m 且长度为 m 的 n-m+1 个子串，看有没有跟模式串匹配的。
每次都比对 m 个字符，要比对 n-m+1 次，这种算法的最坏情况时间复杂度是 O(n*m)。但在实际的开发中，它却是一个比较常用的字符串匹配算法，因为：
第一，实际的软件开发中，大部分情况下，模式串和主串的长度都不会太长。而且每次模式串与 主串中的子串匹配的时候，当中途遇到不能匹配的字符的时候，就可以就停止了，不需要把 m 个字符都比对一下。所以，尽管理论上的最坏情况时间复杂度是 O(n*m)，但是，统计意义上， 大部分情况下，算法执行效率要比这个高很多。
第二，朴素字符串匹配算法思想简单，代码实现也非常简单。简单意味着不容易出错，如果有 bug 也容易暴露和修复。在工程中，在满足性能要求的前提下，简单是首选。这也是我们常说的 KISS（Keep it Simple and Stupid）设计原则 。
所以，在实际的软件开发中，绝大部分情况下，朴素的字符串匹配算法就够用了
4.2 Rabin-Karp 算法
由它的两位发明者 Rabin 和 Karp 的名字来命名，简称RK算法，是BF 算法的升级版。
BF 算法：如果模式串长度为 m，主串长度为 n，那在主串中，就会有（n - m + 1）个长度为 m 的子串，我们只需要暴力地对比这（n - m + 1）个子串与模式串，就可以找出主串 与模式串匹配的子串。但是，每次检查主串与子串是否匹配，需要依次比对每个字符。
BF算法的时间复杂度就比较高 O(n*m)。对朴素的字符串匹配算法稍加改造，引入哈希算法，时间复杂度立刻就会降低。
RK 算法的思路是：通过哈希算法对主串中的（n - m + 1）个子串分别求哈希值，然后逐个与模式串的哈希值比较大小。如果某个子串的哈希值与模式串相等，那就说明对应的子串和模 式串匹配了（这里先不考虑哈希冲突的问题）。
因为哈希值是一个数字，数字之间比较是否相等是非常快速的，所以模式串和子串比较的效率就提高了。
但哈希算法计算子串的哈希值时，需要遍历子串中的每个字符。尽管模式串与子串比较的效率提高了，但是，算法整体的效率并没有提高。提高哈希算法计算子串哈希值的效率：需要巧妙的设计哈希算法。
假设要匹配的字符串的字符集中只包含K个字符，可以用一个K 进制数来表示一个子串，这个K 进制数转化成十进制数，作为子串的哈希值。
比如要处理的字符串只包含 a～z 这 26 个小写字母，就用二十六进制来表示一个字符 串。把 a～z 这 26 个字符映射到 0～25 这 26 个数字，a 就表示 0，b 就表示 1，以此类 推，z 表示 25。
在十进制的表示法中，一个数字的值是通过下面的方式计算出来的。对应到二十六进制，一个包 含 a 到 z 这 26 个字符的字符串，计算哈希的时候，只需要把进位从 10 改成 26 就可以。
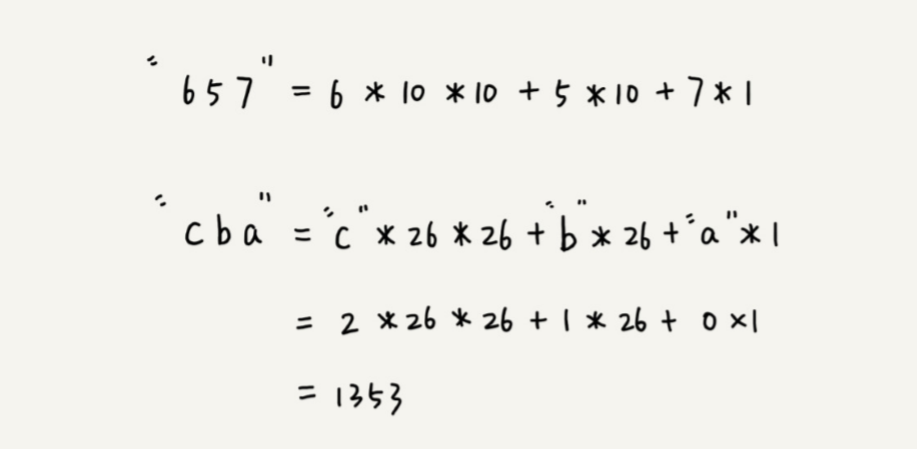
假设字符串中只包含 a～z 这 26 个小写字符，用二十六进制来表示一个字符串，对应的哈希值就是二十六进制 数转化成十进制的结果。 这种哈希算法有一个特点，在主串中，相邻两个子串的哈希值的计算公式有一定关系。
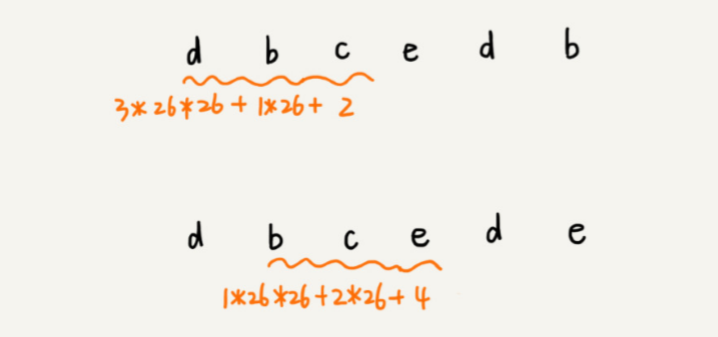
相邻两个子串 s[ i - 1 ] 和 s[ i ]（i 表示子串在主串中的起始位置，子串的长度都为 m），对应的哈希值计算公式有交集，也就是说，可以 使用 s[ i - 1 ] 的哈希值很快的计算出 s[ i ] 的哈希值。用公式表示即：
小细节： 那就是 26(m-1) 这部分的计算，可以通过查表的方法来提高效率。事先计算好 260、261、262……26(m-1)，并且存储在一个长度为m 的数组中，公式中的“次方”就对应数组的下标。当需要计算 26 的 x 次方的时候，就可以从数组的下标为 x 的位置取值，直接使
用，省去了计算的时间。
RK 算法的时间复杂度：
整个 RK 算法包含两部分，计算子串哈希值和模式串哈希值与子串哈希值之间的比较。
- 第一部分，通过设计特殊的哈希算法，只需要扫描一遍主串就能计算出所有子 串的哈希值了，所以这部分的时间复杂度是 O(n)。
- 模式串哈希值与每个子串哈希值之间的比较的时间复杂度是 O(1)，总共需要比较 n-m+1 个子串的哈希值，所以，这部分的时间复杂度也是 O(n)。所以，RK 算法整体的时间复杂度就是 O(n)。
但如果模式串很长，相应的主串中的子串也会很长，通过上面的哈希算法计算 得到的哈希值就可能很大，如果超过了计算机中整型数据可以表示的范围，那该如何解决呢？
刚刚我们设计的哈希算法是没有散列冲突的，也就是说，一个字符串与一个二十六进制数一一对应，不同的字符串的哈希值肯定不一样。因为是基于进制来表示一个字符串的，可以类比成十进制、十六进制来思考一下。实际上，为了能将哈希值落在整型数据范围内，可以牺牲一下，允许哈希冲突。这时如何设计哈希算法？
哈希算法的设计方法有很多，比如假设字符串中只包含 a～z 这 26 个英文字母，那每个字母对应一个数字，比如 a 对应1，b 对应2，以此类推，z 对应26。把字符串中每个字母对应的数字相加，最后得到的和作为哈希值。这种哈希算法产生的哈希值的数据范围就相对要小很多了。
不过这种哈希算法的哈希冲突概率也是挺高的。当然，这只是一个最简单的设计方法，还有很多更加优化的方法，比如将每一个字母从小到大对应一个素数，而不是 1， 2，3……这样的自然数，这样冲突的概率就会降低一些。
那新的问题来了之前只需要比较一下模式串和子串的哈希值，如果两个值相等，那这个子串就一定可以匹配模式串。但是，当存在哈希冲突的时候，有可能存在这样的情况，子串和模式串的哈希值虽然是相同的，但是两者本身并不匹配。解决办法：
当发现一个子串的哈希值跟模式串的哈希值相等时，只需要再对比一下子串和模式串本身即可。如果子串的哈希值与模式串的哈希值不相等， 那对应的子串和模式串肯定也是不匹配的，就不需要比对子串和模式串本身了。
所以，哈希算法的冲突概率要相对控制得低一些，如果存在大量冲突，就会导致 RK 算法的时间 复杂度退化，效率下降。极端情况下，如果存在大量的冲突，每次都要再对比子串和模式串本 身，那时间复杂度就会退化成 O(n*m)。但也不要太悲观，一般情况下，冲突不会很多，RK 算 法的效率还是比 BF 算法高的。
