算法-07| 动态规划
1. 分治 + 回溯 + 递归 + 动态规划
它的本质即将一个复杂的问题,分解成各种子问题,寻找它的重复性。动态规划和分治、回溯、递归并没有很大的本质区别,只是小细节上的不同。
递归
代码模板
public void recur(int level, int param) { // 1.terminator 递归终止条件 if (level > MAX_LEVEL) { // process result return; } // 2.process current logic 处理当前层的逻辑 process(level, param); // 3.drill down 递归到下一层去 recur(level:level + 1, newParam); // 4.restore current status 有时候需要的话即恢复当前层的状态,如果改变的状态都是在参数上,因为递归调用时这个参数是会被复制的,如果是简单变量就不需要恢复这个过程。 }
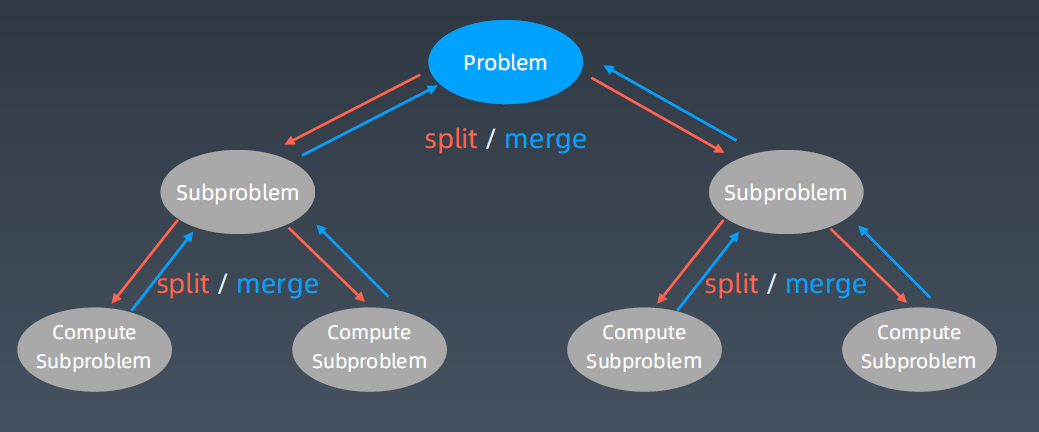
分治 Divide & Conquer
很多大的复杂的问题,它其实都是有所谓的自相似性即重复性,计算机可以飞快地循环运算。
把大的问题分解为几个子问题,同时每个子问题也类似地分解成其他的相同的小的子问题,然后分别运算,再把结果返回,同时把结果聚合在一起
def divide_conquer(problem, param1, param2, ...):
# 1.recursion terminator 递归终止条件
if problem is None:
print_result
return
# 2. prepare data 拆分子问题,
data = prepare_data(problem)
subproblems = split_problem(problem, data)
# conquer subproblems 调子问题的递归函数(调分治函数递归求解) drill down
subresult1 = self.divide_conquer(subproblems[0], p1, ...)
subresult2 = self.divide_conquer(subproblems[1], p1, ...)
subresult3 = self.divide_conquer(subproblems[2], p1, ...)
…
# 3. process and generate the final result 最后将这些结果合并在一块
result = process_result(subresult1, subresult2, subresult3, …)
# 4. revert the current level states 最后有可能当前层的状态需要进行恢复
归并排序即分而治之,分治算法的递归树,分而治之如下:
1. 人肉递归低效、很累
2. 找到最近最简方法,将其拆解成可重复解决的问题(找到重复性,找最近重复性--最大公约数)
3. 养成数学归纳法的思维习惯(抵制人肉递归的诱惑)(先把基础的条件,n=1,n=2时想明白,n成立时,如何推到n+1,比如炮竹的爆炸)
本质:寻找重复性 —> 计算机指令集(if...else,for, 递归)
对递归不熟时,可以人肉递归,画出递归状态树:
如斐波拉契数列递归状态树:
计算第6个数,但它的状态树是2n,它结点(状态树)的扩散是指数级的,所以它的计算复杂度也是指数级

2. 动态规划 Dynamic programming
1. Wiki 定义:
https://en.wikipedia.org/wiki/Dynamic_programming
Dynamic programming,中文翻译叫动态规划,它本质要解决的就是一个递归或分治的问题,它们的不同处在于动态规划它有所谓的最优子结构
2.“Simplifying a complicated problem by breaking it down into
simpler sub-problems”
(in a recursive manner)
用递归的方式,将一个复杂的问题分解为子问题。
3.Divide & Conquer + Optimal substructure
动态规划就是 分治 + 最优子结构
一般动态规划的问题是求一个最优解,或者求一个最大值,或者求一个最少的方式,它有一个最优子结构的存在,每一步不需要把所有的状态都保存下来,只需存最优的状态即可。还需要证明:如果每一步都存一个最优值,最后可以推导出一个全局的最优值。
1)缓存(状态的存储数组)
2)在每一步把次优的状态给淘汰掉,只保留在这一步里面最优或者较优的状态来推导出最后的全局最优。
关键点:
动态规划DP 和 递归或者分治 没有根本上的区别;(DP它的本质就是动态递归,关键看有无最优的子结构)
如果没有最优的子结构,说明所有的子问题都需要计算一遍,同时把最后的结果给合并在一起,就叫分治(每次的最优解就是当前解,它没有所谓的每次比较和淘汰的一个过程)。
共性:找到重复子问题
计算机只会for else loop
差异性:最优子结构、中途可以淘汰次优解
动态规划,有最优子结构,淘汰次优解,这时它的复杂度是更低更有效的,傻递归,傻分治经常是指数级的时间复杂度,如果进行了淘汰次优解,会变成 O(n2) 或者O(n) 时间复杂度。把复杂度从指数级降到了多项式的级别。
斐波拉契数列
斐波拉契数列,傻递归,它的时间复杂度是指数级的,可以递归但是它是指数级的; ---->> 简化(速度上、表达方式上)


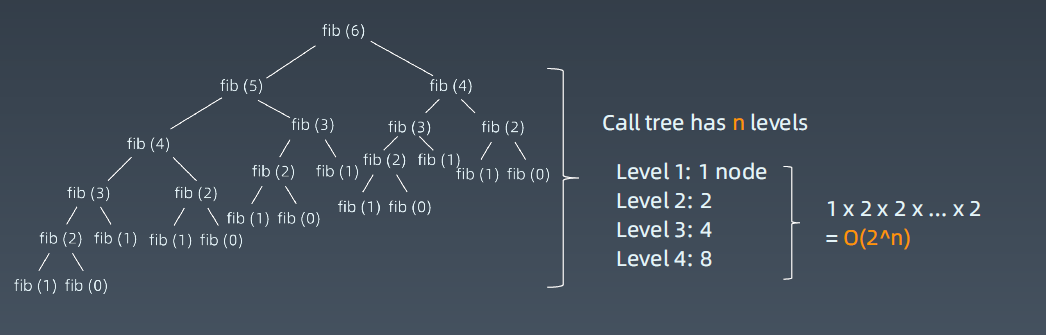
它的状态树为什么是指数级的,它每一层都是指数级的结点:
第一层1个结点,fib(6)
第二层2个,fib(5)、fib(4)
第三次4个,fib(4)、fib(3)、 fib(3)、 fib(2)
...
每一层乘 2,加一起就是2n,所以它是指数级的。
简化:
int fib (int n) { return n <= 1 ? n : fib (n - 1) + fib (n - 2); }
简化代码,并没有改变它的时间复杂度,但是代码清爽一点。
如何改变时间复杂度,加一个缓存,可以存在一个数组里边,这种方法叫记忆化搜索 Memoization。

比如fib(3),第一次计算出来就把fib(3)存在memo里面的3的位置,后边fib(3)就不用计算了直接复用,不然又要从fib(1)和fib(2)算起;
继续将上边代码(逻辑不是特别清洗)优化:
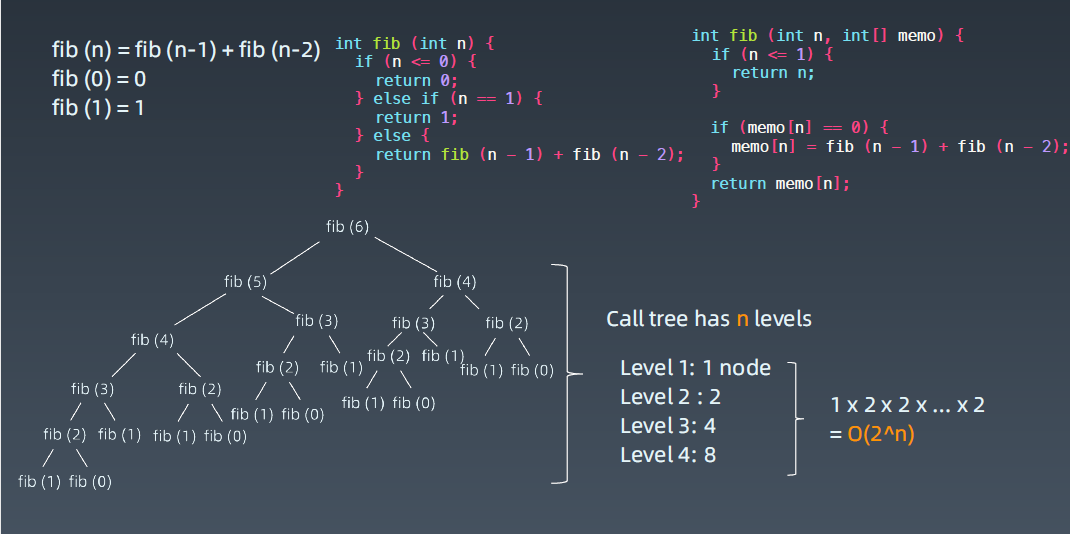
fib (int n, int[] memo) { if (n <= 1) { return n; } if (memo[n] == 0) { //没有被计算过,就从头开始计算并存在数组中,如果 != 0就直接return,把重复的结点就会砍掉,时间复杂度从指数级降为O(n)的时间复杂度。 memo[n] = fib (n - 1) + fib (n - 2); } return memo[n]; }
优化后的:
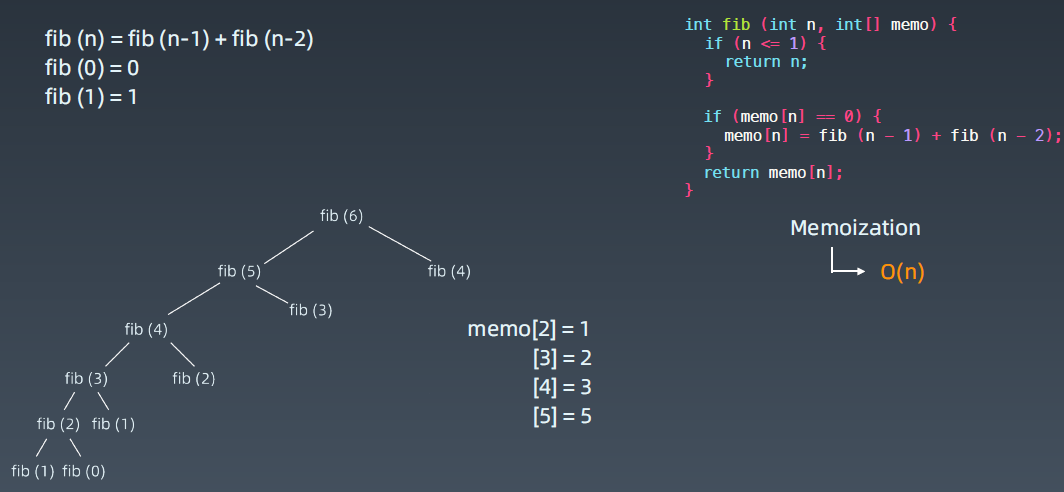
Bottom Up 自底向上
记忆化递归不如直接写一个for循环,
• F[n] = F[n-1] + F[n-2] • a[0] = 0, a[1] = 1; for (int i = 2; i <= n; ++i) { a[i] = a[i-1] + a[i-2]; } • a[n] • 0, 1, 1, 2, 3, 5, 8, 13,
递归,一开始从最上面这个问题开始一步步向下探,最后探到它的叶子结点,叶子结点的值是确定的,<= n 时 return n;
这种方法叫自顶(自顶向下的顺序), 递归 + 记忆化搜索, 也比较符合人脑的思维习惯(要解决fib(6),就算fib(5)和fib(4)...中间结果算过了就直接复用);
从计算机的思维,初始值已经有了,0和1,写fib(6),0,1,1,2,3,5,8,13 0和1相加1,1+1即2, 2+2即4, 2+3即5,...递推...可直接用循环,即自底向上(直接从最下面,循环累加上去即可)。
PS:对于初学者或面试,可以先递归分治然后进行记忆化搜索, 再转化为自底向上的循环;
但对于一个熟练的选手,或者追求DP的功力深厚,尤其在计算机竞赛时,只要开始写递归,所有竞赛选手都可以写for循环,即全部都是自底向上的循环,开始递推。
DP最好的翻译是动态递推,动态规划最终极的一个形态就是自底向上的循环。
路径计数
复杂一点的DP:
1)它的维度变化了,它的状态有时候是二维空间或者三维
2)它中间会有所谓的取舍最优子结构。
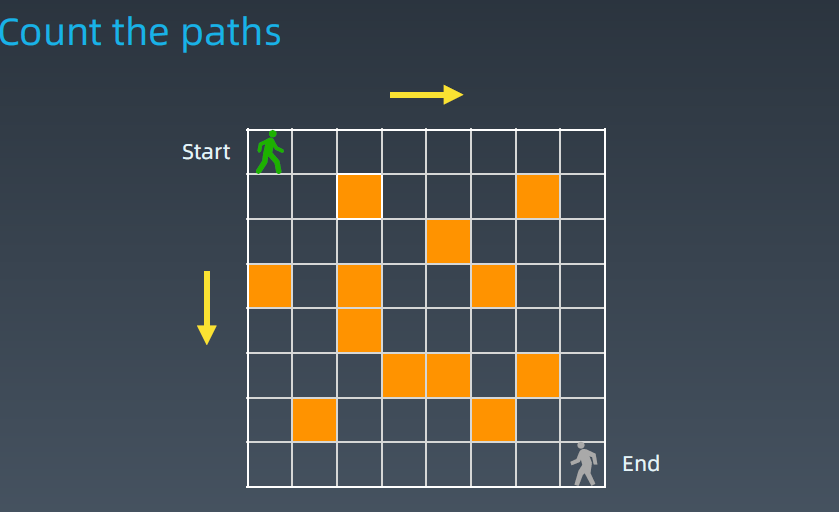
这个人他只能向右或者向下走(不能向左或者向上走),棋盘实心表障碍物不能走,求他从start走到end,有多少种走法?
用分治思想,或者找重复性的思想:
假设棋盘没有障碍物,棋盘大小 1*1, 2*2,....
他只有2中走法,向右到B,向下到A (转化为了2个子问题,从B到End有多少种走法,从A到End有多少种走法, 这两个子问题加起来就是绿人这个大问题的解)
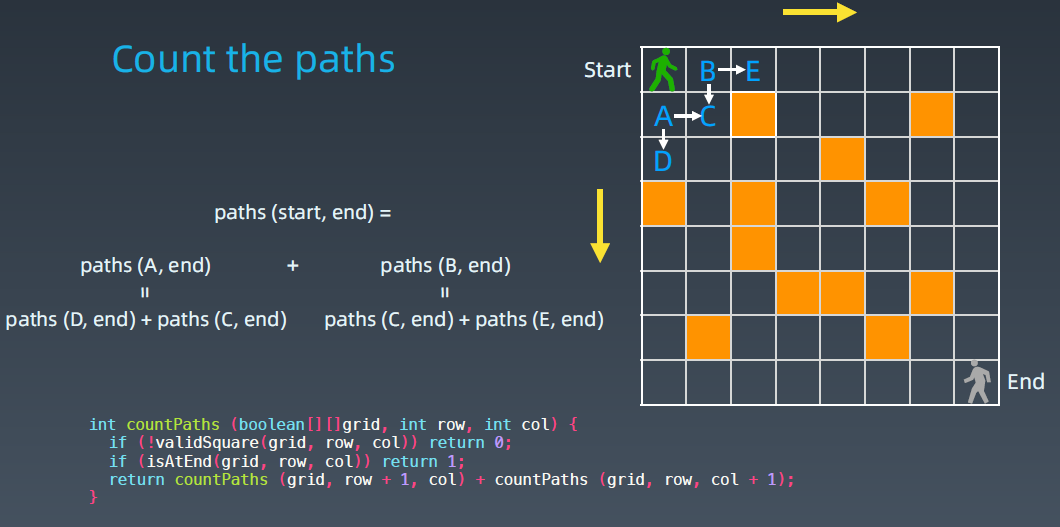
C( Start ---> End) = C(A --> End) + C( B --> End)
有点像斐波拉契数列,只不过它是二维的。
用递推的思想:

自底向上推:
把靠近End的格子全推一遍,向右走,那一排都是1,不能往下走,往下走就出去了;同理可得上边一排也全都是1
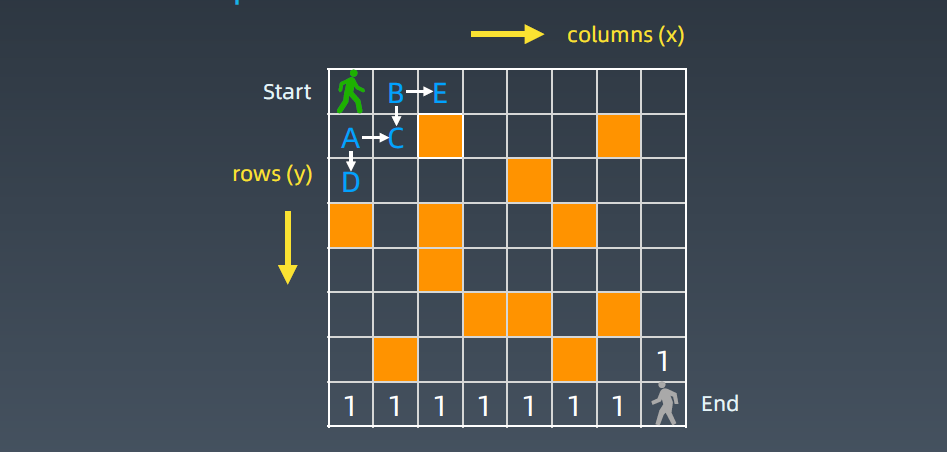
看任何一个空格子,它的走法 = 右边格子走法 + 下边格子的走法
如果格子是石头,那么它的走法即是0,得到一个递推公式:
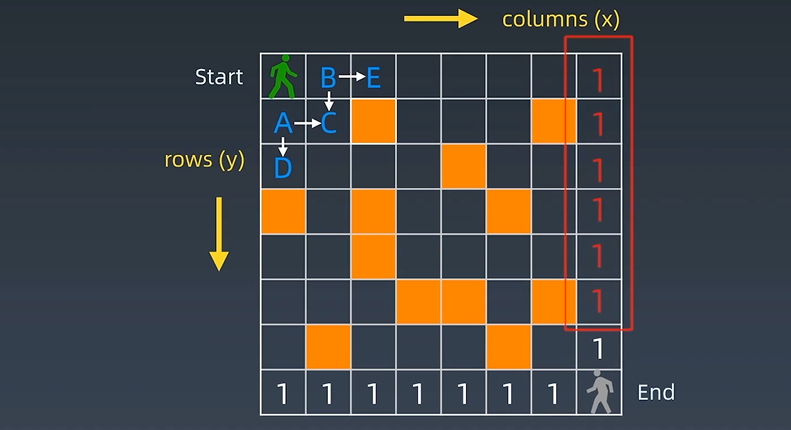
状态转移方程(DP方程) opt[i , j] = opt[i + 1, j] + opt[i, j + 1] 完整逻辑: if a[i, j] = ‘空地’: opt[i , j] = opt[i + 1, j] + opt[i, j + 1] else: opt[i , j] = 0

绿人从Start 到End 走法 = 17 + 10 = 27
通过递推只要保证初始值是对的,逻辑就是 右 + 下; 这就是数学归纳法的思维。
动态规划关键点:
1. 最优子结构 opt[n] = best_of(opt[n-1], opt[n-2], …) (推导出的第n步它的值是前面几个值的最佳值,这个最佳值有时候就是简单累加,有时取最大值或最小值)
2. 储存中间状态:opt[i] (必须定义和存储这个中间态,这个跟分治是有区别的,分治一般把这步放递归里边了,)
3. 递推公式(美其名曰:状态转移方程或者 DP 方程)
Fib: opt[i] = opt[n-1] + opt[n-2]
二维路径:opt[i,j] = opt[i+1][j] + opt[i][j+1] (且判断a[i,j]是否空地)
DP,它有一个筛选过程,上例是累加,有可能是最大值或最小值,
最长公共子序列
斐波拉契数列是一维数组的简单DP,不同路径是二维数组的DP
最长公共子序列是 字符串进行变化的DP,要进行思维层级的转换,当进行DP时,它已不是一个简单的字符串,扩展为一个二维数组来定义状态,前两个题目状态的定义相对简单,即它本身的数组的结构,以及棋盘的二维数组结构即状态空间,状态数组。
最长公共子序列:给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。 例如:
输入:text1 = "abcde", text2 = "ace" 输出:3 解释:最长公共子序列是 "ace",它的长度为 3。
方法一暴力求解: 枚举它所有的子序列,看这个子序列是否也在第二个里面也是子序列,对text1中每个字母都是取或不取,就生产一个子序列,看这个子序列是否也在text2中存在,一个个字母对比看是否在text2中。这种办法的时间复杂度是2n, 枚举每一个就像括号问题(左括号 右括号)。
方法二 找重复性
1. S1 = “”
S2 = 任意字符串
2. S1 =“A”
S2 = 任意
3. S1 =“…….A”
S2 = “.….A”
假设两个text都为空,最长公共子序列就是空;假设一个为空,另外一个为任意字符串,最长公共子序列也是空;
假设S1 = “A”,S2为任意字符串,看A是否存在S2中,只要存在最长公共子序列就是1,否则0;
假设S1为“....A”,S2也是“....A”, 第一种经验是从最后一个字符开始看,第二个经验是比较这两个字符串A之前是否存在最长公共子序列,存在再 + 1,第三个经验就是把它们转化为二维数组的行和列。
两个字符串: "ABAZDC", "BACBAD",把它们一个在行上排列,一个在列上面排下来。
行列相交的值就是公共子序列,如下图中4,即text1 C -> A 和text2 D -> B的公共子序列。

先初始化,行 0 1 1 1 1 ...(比如行A与列B为0,行A B 与列B为1, 行A B A 与列B为1...), 列 0 1 1 1 1 ...;
后边的进行递推,假设最后一个字符都相同S1 =“…….A”,S2 = “.….A”,即前面前缀的子问题 再 +1,否则,S1的“.......” 与S2的A 减1 或者 S2的 “.....”与 S1的A 减1;
比如第2行,第2列的1,它们的最后一个字符不相同,就变成text1中A B 和text2中B的最长公共子序列1 或者 text2中B A和text1中A的最长公共子序列1 。
第3行,第6列的3,它最后一个字符都是C,就转化为求3之前的字符串的最长公共子序列,求text1 A B A Z D和 text2 B A它们的最长公共子序列;
子问题:
• S1 = “ABAZDC”
S2 = “BACBAD”
• If S1[-1] != S2[-1]: LCS[s1, s2] = Max(LCS[s1-1, s2], LCS[s1, s2-1]) //S1和 S2最后一个字符不相同, -1表最后一个字符,python的写法 或java中S1.length - 1
// S1去掉一个字符和S2比较,或者S2去掉一个字符和S1比较,它们之间的最长公共子序列的子问题,从中再选一个较大者
LCS[s1, s2] = Max(LCS[s1-1, s2], LCS[s1, s2-1], LCS[s1-1, s2-1])
• If S1[-1] == S2[-1]: LCS[s1, s2] = LCS[s1-1, s2-1] + 1
LCS[s1, s2] = Max(LCS[s1-1, s2], LCS[s1, s2-1], LCS[s1-1, s2-1], LCS[s1-1][s2-1] + 1)
DP方程:
• If S1[-1] != S2[-1]: LCS[s1, s2] = Max(LCS[s1-1, s2], LCS[s1, s2-1])
• If S1[-1] == S2[-1]: LCS[s1, s2] = LCS[s1-1, s2-1] + 1
1. 打破自己的思维惯性,形成机器思维(找重复性);
2. 理解复杂逻辑的关键;
3. 也是职业进阶的要点要领;
动态规划的思维要点:
①化繁为简成为各种子问题; ② 定义好状态空间; ③动态规划的方程即DP方程。

5 easy steps to dp:
- ① define subproblems(分进分治,把当前复杂问题转换成一个简单的子问题)
- ② guess(part of solution)(猜递推方程是如何递推的)
- ③ relate subproblem solutions (把子问题的解合并起来 merge)
- ④ recurse & memoize (递归转成记忆化搜索或者 把DP的状态表建立起来, 自底向上进行递推)
- ⑤ solve original problem (废话)
①②③就是分治的思想,找重复性(计算机的指令只能循环或递归)
第一步分治找它的重复性和子问题;
第二步定义出状态空间, 可以用记忆化搜索递归, 或者从下到上进行DP的顺推, 自底向上进行推导;
三角形最小路径和
1. brute-force,递归,n层可以左或者可以右; 时间复杂度是2^n
2. DP:
a. 重复性(分治); (类似于不同路径问题) problem(i, j) = min(sub(i+1, j), sub(i+1, j+1)) + a[i, j]
b. 定义状态数组; f[i, j]
c. DP方程; f[i, j] = min(f[i+1, j], f[i+1, j+1]) + a[i, j]
最大子序和
1. 暴力求解: n^2
2. DP:
a. 分治(子问题) max_sum(i) = Max( max_sum( i - 1 ), 0 ) + a[ i ]
b. 状态数组定义 f[ i ]
c. DP方程 f[ i ] = Max( f [ i - 1 ], 0 ) + a[ i ]
1. dp问题,公式为:dp[i] = max((nums[i], nums[i] + dp[i - 1]))
2. 最大子序和 = 当前元素自身最大, 或者包含之前的sum+自己的最大
Coin change
状态树

1. 暴力:递归-时间复杂度指数级
2. BFS
3. DP(与上楼梯或者斐波拉契数列差不多)
a.subproblems
b.DP array :
f(n) = f(n-1) + f(n-2) + f(n-3)每次走一步或者走两步或者走三步,它是一个累加的
这里不再是1 2 3常量, 变成了一个数组,f(n)表凑成面值为n所需的最小硬币数量,它取自于k的面值 f(n) = f(n-k) k在数组里边取所有值;
f(n) = min{(f(n-k), for k in [1,2,5]}) + 1,加1是因为最少需要一个硬币,这个硬币的面值就是k
c.DP方程
打家劫舍
DP: a. 子问题 b. 状态定义 c. DP方程 数组a表示偷盗从0开始一直到第i个房子它最大可以偷的金额是多少, 返回的结果是a[n-1] 第一维表房子的下标,再加一维表示是否被偷:a[i][0, 1], 0 i表偷、 1 i表不偷 状态转移方程: a[i]表示从0到第i个房子能偷到的房子的最大值, 同时第i个房子不偷; a[i][0] = Max(a[i-1][0], a[i-1][1]) //表一直到第i个房子,且第i个房子不偷, i-1个房子不偷或者i-1个房子偷的最大值,但不偷第i个房子 a[i][1] = a[i-1][0] + nums[i] //第i个房子偷,i-1个房子只能不偷,当前的房子偷 简化操作: a[i]表0-i天,且nums[i]必偷的最大值, 结果就是max(a) 状态方程: a[i] = Max(a[i-1], a[i-2] + nums[i]) 第i-1天必偷就不能偷i天了,或者第i-2最大值或i-2天偷了 则就可以偷num[i]了 ; 所有都是正整数


