数据结构-03| 跳表
1. 跳表Skip List
二分查找底层依赖的是数组随机访问的特性， 所以只能用数组来实现。如果数据存储在链表中，就真的没法用二分查找算法了吗？实际上，我们只需要对链表稍加改造，就可以支持类似“二分”的查找算法。
我们把改造之后的 数据结构叫作跳表（Skip list）。
跳表是一种各方面性能都比较优秀的动态数据结构，可以支持快速的插入、删除、查 找操作，写起来也不复杂，甚至可以替代红黑树（Red-black tree）。
Redis 中的有序集合（Sorted Set）就是用跳表来实现的。红黑树也可以实现快速的插入、删除和查找操作。那 Redis 为什么会选择用跳表来实现有序集合呢？ 为什么不用红黑树呢
在redis中运用，这种数据结构是为了补足链表的缺陷（lookup时间复杂度是O(n)，究其本质它是一个简单的线性一维的结构 ）而设计出来的；
2. 链表加速 --> 跳表
对于一个单链表来讲，即便链表中存储的数据是有序的，如果我们要想在其中查找某个数据，也 只能从头到尾遍历链表。这样查找效率就会很低，时间复杂度会很高，是 O(n)。
那么如何给链表加速，加快它的查询效率呢：
它所谓的优化思想就是 升维，或者叫以空间换时间。
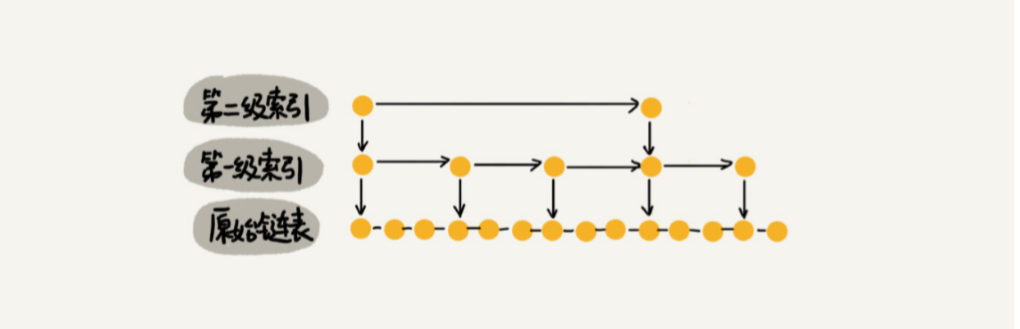
对链表建立一级“索引”，每两个结点提取一个结点到上一级，把抽出来的那一级叫作索引或索引层。图中的 down 表示 down 指针，指向下一级结点。
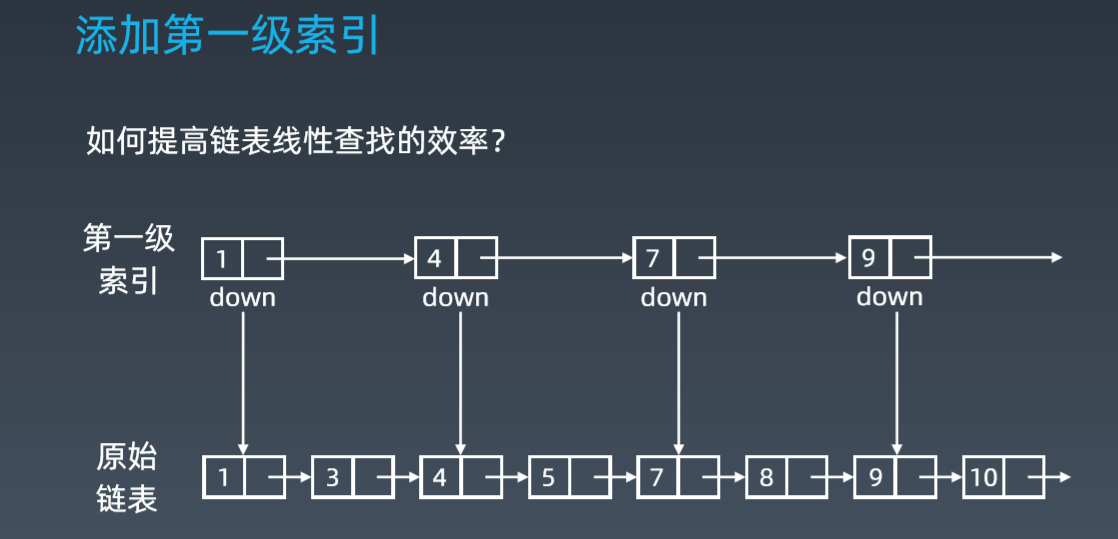
比如我们要查找节点10，先在索引层遍历，当遍历到索引层中数值为9时，通过索引层结点的 down 指针，下降到原始链表这一层，继续遍历。这个时候，我们只需要 再遍历 1 个结点，就可以找到值等于 10
的这个结点了。这样，原来如果要查找 10，需要遍历 8 个结点，现在只需要遍历 5 个结点。
加一层索引之后，查找一个结点需要遍历的结点个数减少了，也就是说查找效率提高了。那如果我们再加一级索引呢？
索引，增加一级索引（指向头指针，它的下一个位置是指向next + 1的位置），索引是基于链表，链表是走向NEXT，它这里走向NEXT + 1即两倍的NEXT；也认为NEXT的速度是1，索引的每次速度是2。
二级索引是在一级索引的基础之上 * 2：
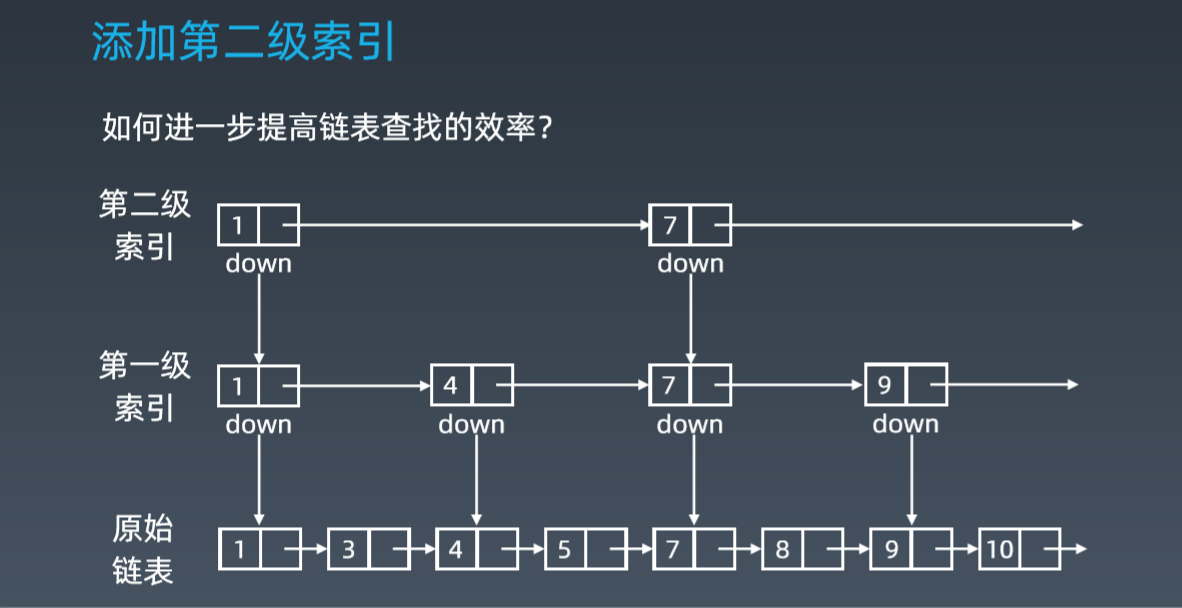
二级索引每次跨四个元素，是一级索引速度的2倍；要查找7这个元素直接就跨过来了。
现在我们再来查找 10，只需要遍历 4 个结点了，需要遍历的结点数量又减少了。
以此类推，可以增加多级索引。
上面的例子数据量不大，所以即便加了两级索引，查找效率的提升也并不明显。下图是一个包含 64 个结点的链表，按照前面讲的这种思路，建立了 五级索引。
从图中可以看出，原来没有索引的时候，查找 62 需要遍历 62 个结点，现在只需要遍历 11 个结点，速度是不是提高了很多？所以，当链表的长度 n 比较大时，比如 1000、10000 的时 候，在构建索引之后，查
找效率的提升就会非常明显。
增加log2n个索引； 从一维变成了二维（如果升成三维空间按理说会更快）；同理运用了更多的节点，它的空间消耗会比一维的更大，空间换时间的策略。
3. 跳表的时间复杂度分析
在一个 单链表中查询某个数据的时间复杂度是 O(n)。那在一个具有多级索引的跳表中，查询某个数据 的时间复杂度是多少呢？
如果链表里 有 n 个结点，会有多少级索引呢？
每两个结点会抽出一个结点作为上一级索引的结点，那第一级索引的结点个数大约就是 n/2，第二级索引的结点个数大约就是 n/4，第三级索引的结点个数大约就是 n/8， 依次类推，也就是说，第 k 级索引的结
点个数是第 k-1 级索引的结点个数的 1/2，那第 k级索 引结点的个数就是 n/(2h )。
假设索引有 h 级，高级的索引有 2 个结点。通过上面的公式，我们可以得到 n/(2h )=2，从而 求得 h=log2 n-1。如果包含原始链表这一层，整个跳表的高度就是 log 2n。我们在跳表中查询 某个数据的时候，如
果每一层都要遍历 m 个结点，那在跳表中查询一个数据的时间复杂度就是 O(m*logn)。
那这个 m 的值是多少呢？按照前面这种索引结构，我们每一级索引都多只需要遍历 3 个结 点，也就是说 m=3，为什么是 3 呢？我来解释一下。
2h = n / 2 --- > h = 1 / 2 log2n = log2n - 1
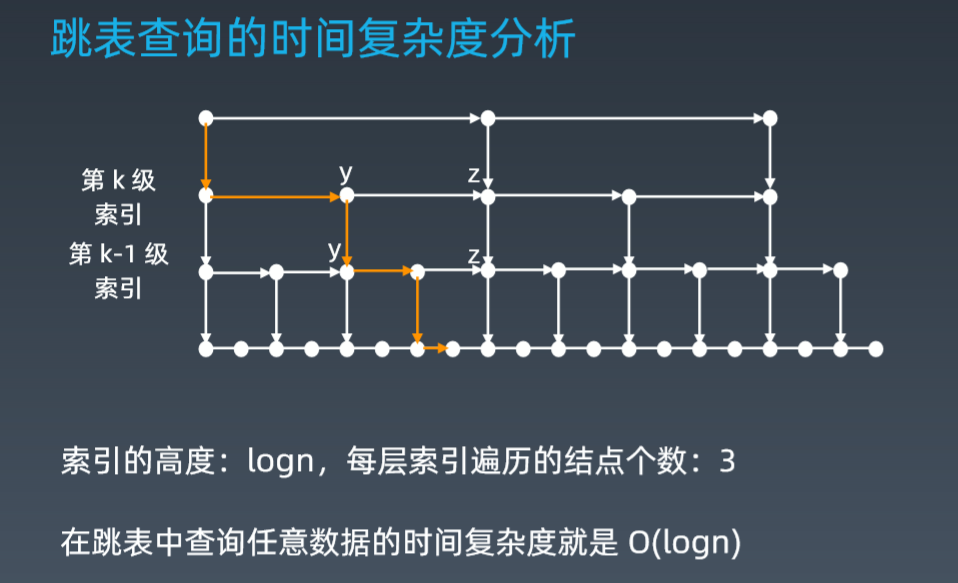
假设我们要查找的数据是 x，在第 k 级索引中，我们遍历到 y 结点之后，发现 x 大于 y，小于后 面的结点 z，所以我们通过 y 的 down 指针，从第 k 级索引下降到第 k-1 级索引。在第 k-1 级 索引中，y 和 z 之间
只有 3 个结点（包含 y 和 z），所以，我们在 K-1 级索引中多只需要遍 历 3 个结点，依次类推，每一级索引都多只需要遍历 3 个结点。
得到 m=3，所以在跳表中查询任意数据的时间复杂度就是 O(logn)。这 个查找的时间复杂度跟二分查找是一样的。换句话说，我们其实是基于单链表实现了二分查找， 不过，天下没有免费的午
餐，这种查询效率的提升，前提是建立了很多级索引， 也就是空间换时间的设计思路。
4. 跳表的空间复杂度
比起单纯的单链表，跳表需要存储多级索引，肯定要消耗更多的存储空间。那到底需要消耗多少 额外的存储空间呢？
假设原始链表大小为 n，那第一级索引大约有 n/2 个结点，第二级索引大约有 n/4 个结点，以此类推，每上升一级就减少一半，直到剩下 2 个结点。如果我们把每层索引的结点数写出来，就是一个等比数列。
这几级索引的结点总和就是 n/2+n/4+n/8…+8+4+2=n-2。所以，跳表的空间复杂度是 O(n)。也就是说，如果将包含 n 个结点的单链表构造成跳表，我们需要额外再用接近 n 个结点 的存储空间。那我们有没有办
法降低索引占用的内存空间呢？
前面都是每两个结点抽一个结点到上级索引，如果我们每三个结点或五个结点，抽一个结点 到上级索引，是不是就不用那么多索引结点了呢？
从图中可以看出，第一级索引需要大约 n/3 个结点，第二级索引需要大约 n/9 个结点。每往上 一级，索引结点个数都除以 3。为了方便计算，我们假设高一级的索引结点个数是 1。我们把每级索引的结点个数都
写下来，也是一个等比数列。
通过等比数列求和公式，总的索引结点大约就是 n/3+n/9+n/27+…+9+3+1=n/2。尽管空间 复杂度还是 O(n)，但比上面的每两个结点抽一个结点的索引构建方法，要减少了一半的索引结 点存储空间。
实际上，在软件开发中，我们不必太在意索引占用的额外空间。在讲数据结构和算法时，我们习惯性地把要处理的数据看成整数，但是在实际的软件开发中，原始链表中存储的有可能是很大的 对象，而索引结
点只需要存储关键值和几个指针，并不需要存储对象，所以当对象比索引结点大 很多时，那索引占用的额外空间就可以忽略了。
5. 高效的动态插入和删除
跳表的查找如上。实际上，跳表这个动态数据结构，不仅支持查找操作，还支持动态的插入、删除操作，而且插入、删除操作的时间 复杂度也是 O(logn)。
如何在跳表中插入一个数据，以及它是如何做到 O(logn) 的时间复杂度的？
在单链表中，一旦定位好要插入的位置，插入结点的时间复杂度是很低的，就是 O(1)。但是，这里为了保证原始链表中数据的有序性，我们需要先找到要插入的位置，这个查找操作就会比较耗时。
对于纯粹的单链表，需要遍历每个结点，来找到插入的位置。但是，对于跳表来说，查找某个结点的的时间复杂度是 O(logn)，所以这里查找某个数据应该插入的位置，方法也是类似的，时间复杂度也是O(logn)。
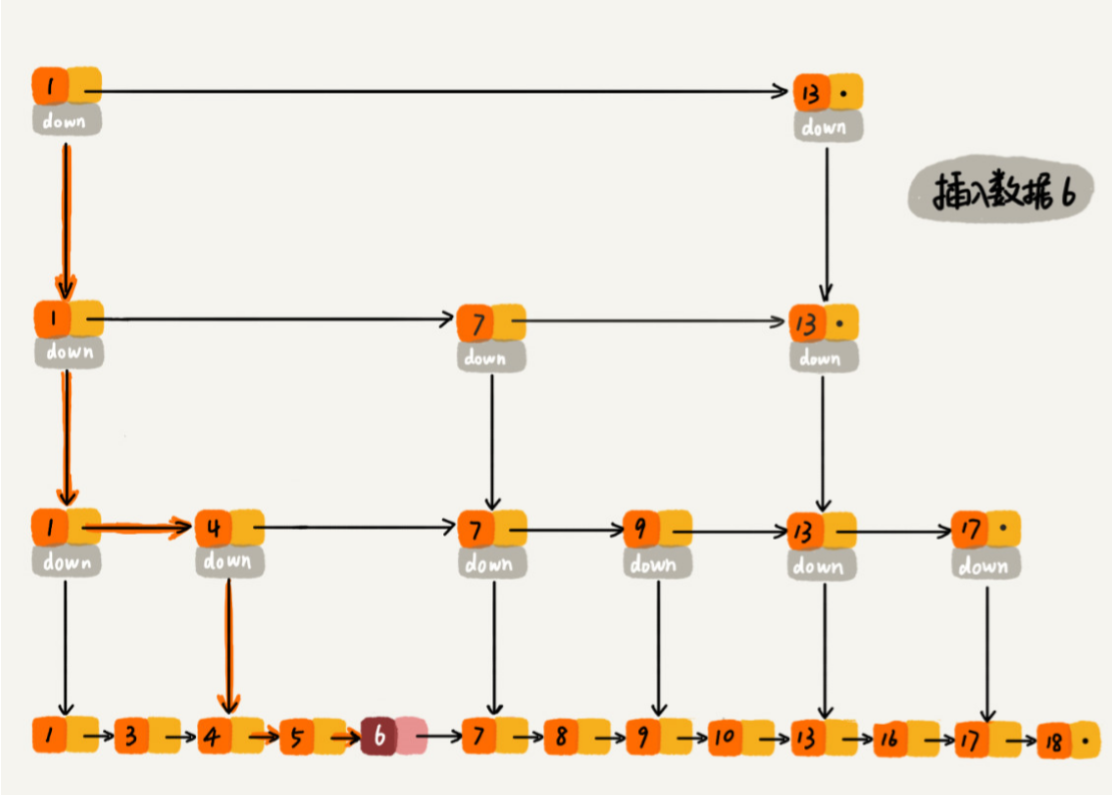
删除操作
如果这个结点在索引中也有出现，我们除了要删除原始链表中的结点，还要删除索引中的。因为单链表中的删除操作需要拿到要删除结点的前驱结点，然后通过指针操作完成删除。所以在查找要删除的结点的时
候，一定要获取前驱结点。当然，如果我们用的是双向链表，就不需要考虑这个问题了。
6. 跳表索引动态更新
当我们不停地往跳表中插入数据时，如果我们不更新索引，就有可能出现某 2 个索引结点之间 数据非常多的情况。极端情况下，跳表还会退化成单链表。
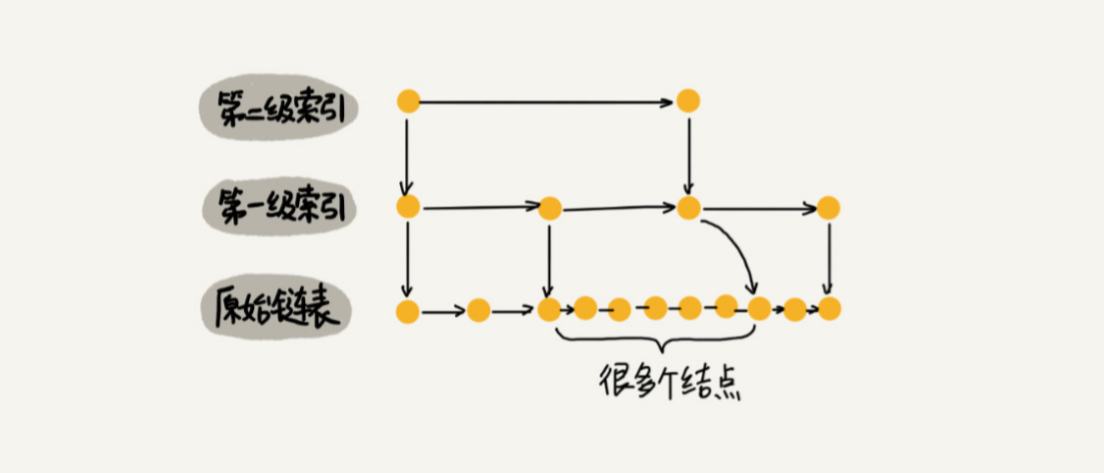
作为一种动态数据结构，我们需要某种手段来维护索引与原始链表大小之间的平衡，也就是说， 如果链表中结点多了，索引结点就相应地增加一些，避免复杂度退化，以及查找、插入、删除操 作性能下降。
红黑树、AVL 树这样平衡二叉树，它们是通过左右旋的方式保持左右子树 的大小平衡，而跳表是通过随机函数来维护前面提到 的“平衡性”。
当我们往跳表中插入数据的时候，我们可以选择同时将这个数据插入到部分索引层中。如何选择加入哪些索引层呢？
我们通过一个随机函数，来决定将这个结点插入到哪几级索引中，比如随机函数生成了值 K，那我们就将这个结点添加到第一级到第 K 级这 K 级索引中。
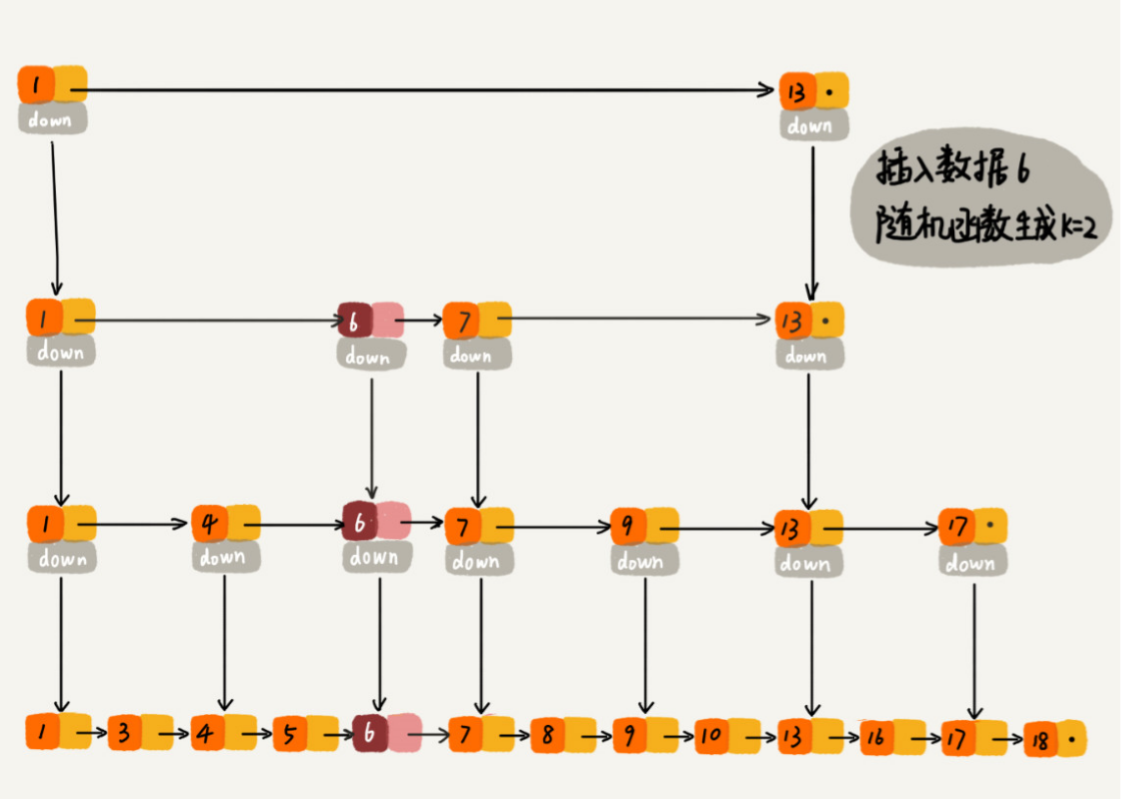
随机函数的选择很有讲究，从概率上来讲，能够保证跳表的索引大小和数据大小平衡性，不至于性能过度退化。至于随机函数的选择，可以查看Redis 中关于有序集合的跳表实现。
跳表的实现还是稍微有点复杂的
工程中的运用：
那 Redis 为什么会选择用跳表来实现有序集合呢？ 为什么不用红黑树呢
Redis 中的有序集合是通过跳表来实现的，严格点讲，其实还用到了散列表。如果你去查看 Redis 的开发手册，就会发现， Redis 中的有序集合
支持的核心操作主要有下面这几个：
- 插入一个数据；
- 删除一个数据；
- 查找一个数据；
- 按照区间查找数据（比如查找值在 [100, 356] 之间的数据）；
- 迭代输出有序序列。
其中，插入、删除、查找以及迭代输出有序序列这几个操作，红黑树也可以完成，时间复杂度跟 跳表是一样的。但是，按照区间来查找数据这个操作，红黑树的效率没有跳表高。
对于按照区间查找数据这个操作，跳表可以做到 O(logn) 的时间复杂度定位区间的起点，然后在原始链表中顺序往后遍历就可以了。这样做非常高效。
当然，Redis 之所以用跳表来实现有序集合，还有其他原因，比如，跳表更容易代码实现。虽然跳表的实现也不简单，但比起红黑树来说还是好懂、好写多了，而简单就意味着可读性好，不容易出错。还有，跳
表更加灵活，它可以通过改变索引构建策略，有效平衡执行效率和内存消耗。
不过，跳表也不能完全替代红黑树。因为红黑树比跳表的出现要早一些，很多编程语言中的 Map 类型都是通过红黑树来实现的。我们做业务开发的时候，直接拿来用就可以了，不用费劲 自己去实现一个红黑
树，但是跳表并没有一个现成的实现，所以在开发中，如果你想使用跳表， 必须要自己实现。
LRU Cache - Linked list
https://www.jianshu.com/p/b1ab4a170c3c
https://leetcode-cn.com/problems/lru-cache
Redis - Skip List
https://redisbook.readthedocs.io/en/latest/internal-datastruct/ skiplist.html
https://www.zhihu.com/question/20202931
