数据结构-06 | 平衡二叉查找树| AVL树| 红黑树
1. 树Tree
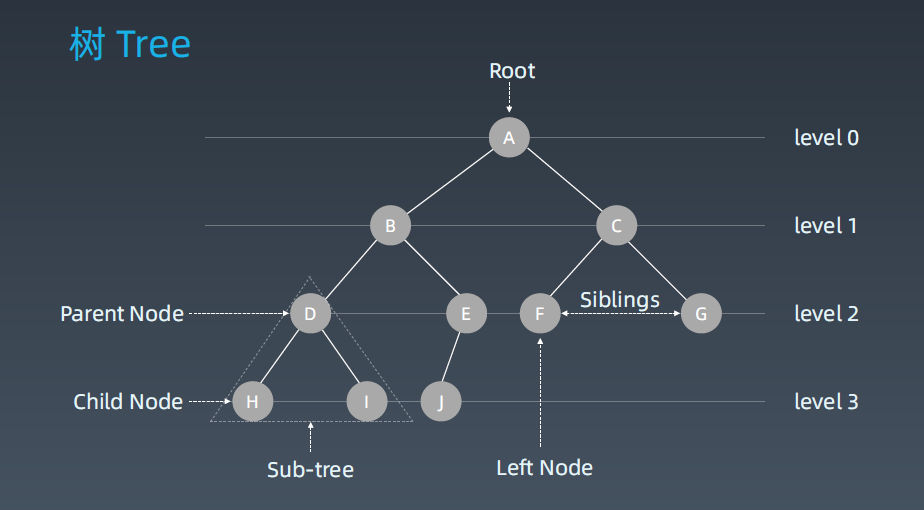
2. 二叉树 Binary Search
二叉树遍历
Pre-order/In-order/Post-order
- 1. 前序(Pre-order)：根-左-右
- 2. 中序(In-order)：左-根-右 （如果一棵树是二叉搜索树，它的中序是有序的）
- 3. 后序(Post-order)：左-右-根
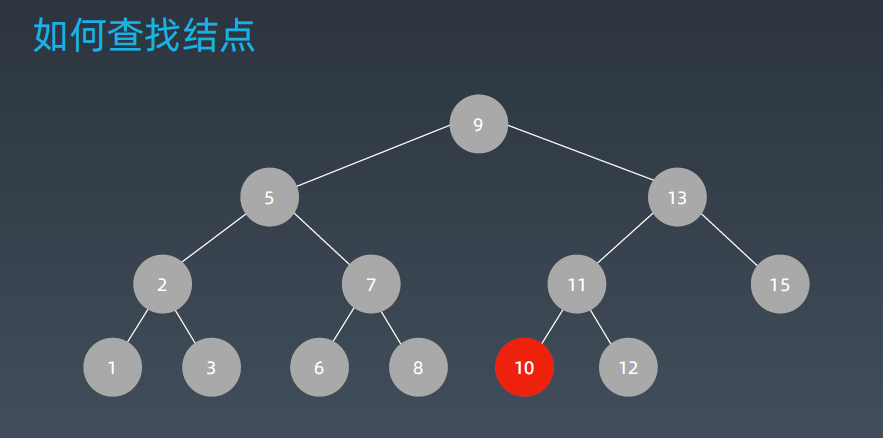
3. 二叉搜索树 Binary Search Tree
树和链表没有本质的区别，当一个链表分出两个next时就把它称为树，从一维空间扩展为二维空间了。
这种扩展的好处：引入了二叉搜索树，当它本身是有序的话可以根据它和当前结点的大小关系分出来它只走左分支还是右分支（它的查询、插入和搜索的效率就是从O(n)变成Log(2n)的时间复杂度 ）。
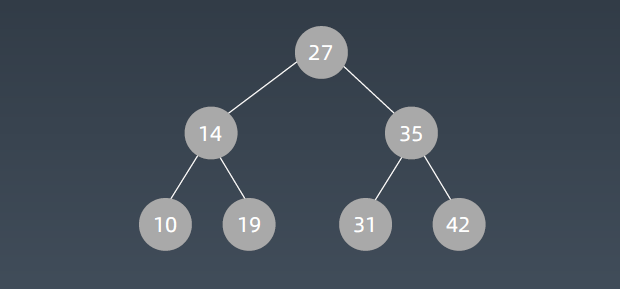
二叉搜索树，也称二叉搜索树、有序二叉树（Ordered Binary Tree）、 排序二叉树（Sorted Binary Tree），
是指一棵空树或者具有下列性质的二叉树：
1. 左子树上所有结点的值均小于它的根结点的值；
2. 右子树上所有结点的值均大于它的根结点的值；
3. 以此类推：左、右子树也分别为二叉查找树。 （这就是 重复性！）
二叉搜索树的中序遍历是：升序排列
二叉搜索树的查找、插入、删除等操作
二叉搜索树即二叉查找树是最常用的一种二叉树，它支持快速插入、删除、查找操作，各个操作的时间复杂度跟树的高度成正比，理想情况下，时间复杂度是 O(logn) 。
不过，二叉查找树在频繁的动态更新过程中，可能会出现树的高度远大于 log2n 的情况，从而导致各个操作的效率下降。极端情况下，二叉树会退化为链表，时间复杂度会退化到 O(n)。
要解决这个复杂度退化的问题，需要设计一种平衡二叉查找树。
它的时间复杂度为Log(2n)，n为它的结点个数。
极端情况下，一直插入到左边，二叉搜索树就退化成了链表，就类似于链表的查询时间复杂度了。
保证性能的关键
1. 保证二维维度！ —> 左右子树结点平衡（recursively）
2. Balanced
4. 平衡二叉树
二叉查找树是常用的一种二叉树，它支持快 速插入、删除、查找操作，各个操作的时间复杂度跟树的高度成正比，理想情况下，时间复杂度 是 O(logn)。
不过，二叉查找树在频繁的动态更新过程中，可能会出现树的高度远大于 log n 的情况，从而 导致各个操作的效率下降。极端情况下，二叉树会退化为链表，时间复杂度会退化到 O(n)。要解决这个复杂度退化
的问题，我们需要设计一种平衡二叉查找树。
但凡讲到平衡二叉查找树，就会拿红黑树作为例子。在工程中，很多用到平衡二叉查找树的地方都会用红黑树。 为什么工程中都喜欢用红黑树，而不是其他平衡二叉查找树呢？
平衡二叉树定义：二叉树中任意一个节点的左右子树的高度相差不能大于 1。从这个定义来看，完全二叉树、满二叉树其实都是平衡二叉树，但是非完全二叉树也有可能是平衡二叉树。
平衡二叉查找树不仅满足上面平衡二叉树的定义，还满足二叉查找树的特点。
最先被发明的平衡二叉查找树是AVL 树，它严格符合平衡二叉查找树的定义，即任何节点的左右子树高度相差不超过 1，是一种高度平衡的二叉查找树。
但很多平衡二叉查找树其实并没有严格符合上面的定义（树中任意一个节点的左右子树的高度相差不能大于 1），比如红黑树，它从根节点到各个叶子节点的最长路径，有可能会比最短路径大一倍。
对于平衡二叉查找树这个概念，从他的由来，去理解“平衡”的意思。发明平衡二叉查找树这类数据结构的初衷是解决普通二叉查找树在频繁的插入、删除等动态更 新的情况下，出现时间复杂度退化的问题。
平衡二叉查找树中“平衡”的意思，其实就是让整棵树左右看起来比较“对称”、比较“平衡”，不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一些，相应的插入、删除、查找等操作的效率高一些。
所以，如果设计一个新的平衡二叉查找树，只要树的高度不比 log2n 大很多（比如树的高度仍然是对数量级的），尽管不符合严格的平衡二叉查找树的定义，但仍可说，这是一个合格的平衡二叉查找树。
AVL、 红黑树
Splay Tree（伸展树）、Treap（树堆）
B+ 树，二三树
①从7位置打折，34567， 8912
②相应的每个左右子树也类似的做下去。 这样就可以让整个树变得平衡。
但是不会等到它真正的自平衡二叉树里面（AVL、红黑树） 不会等到这个树病入膏肓了，再去平衡。而是在每一步进行插入或者删除的时候，都去判断它是否平衡，以及将它维护成二叉平衡树的状态。
5. AVL树
1. 发明者 G. M. Adelson-Velsky 和 Evgenii Landis
2. Balance Factor（平衡因子）：
是它的左子树的高度减去它的右子树的高度（有时相反）。 （因为二叉搜索树查询效率只与高度有关，和它节点的个数是没关的）
balance factor = {-1, 0, 1}
3. 通过旋转操作来进行平衡（四种）
Self-balancing binary search tree
5.1 平衡因子
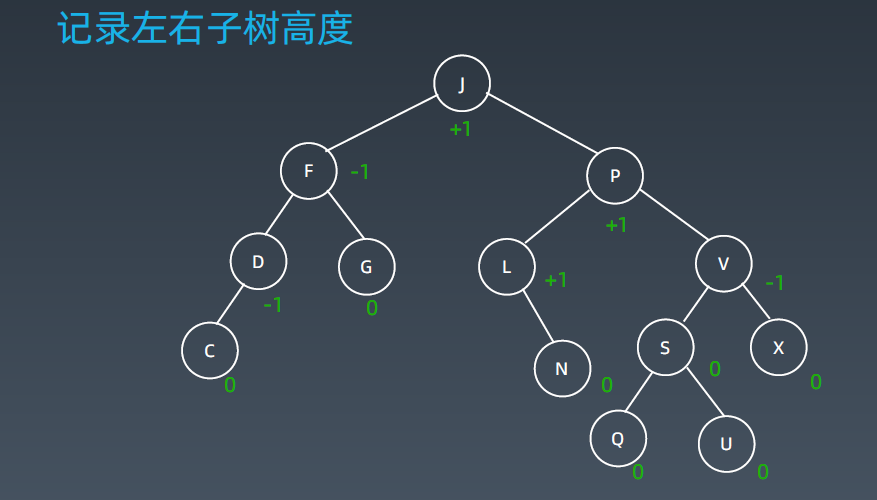
所有叶子节点高度都是0，根结点J （平衡因子 = 右子树高度 - 左子树高度 4 - 3 = +1），
上图这颗树是一个严格的平衡AVL，它的平衡因子在 -1 0 1之间。保持平衡因子不超过绝对值 1就变成了一颗二叉搜索树。
开始最直观也是最自然的一种维护方式：
最开始最经典的AVL树，它始终要保证任何一个结点它的平衡因子都只在 0 -1 1 ，这样就可以维护它的效率。
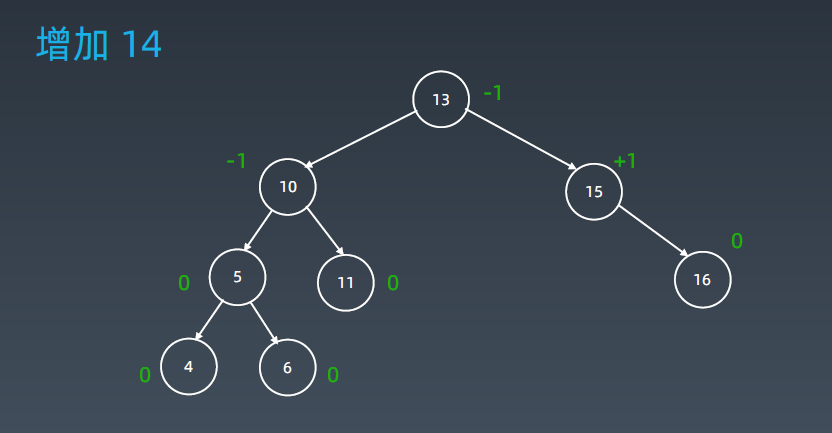
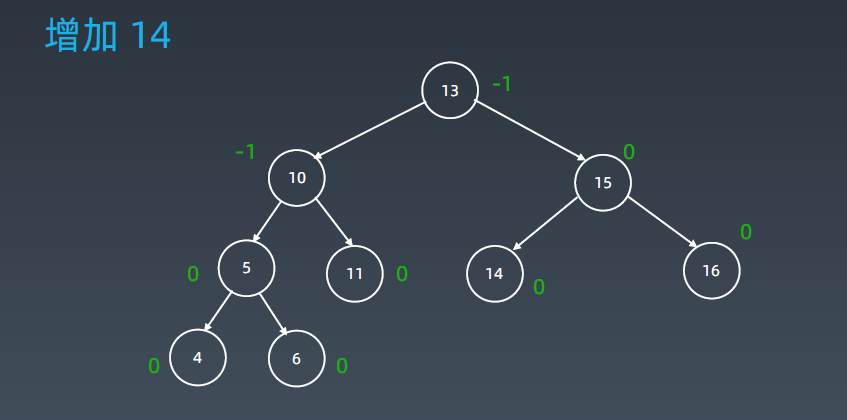
这时它的平衡因子的范围不在是1的范围了，变成-2了。接下来就要进行旋转操作：
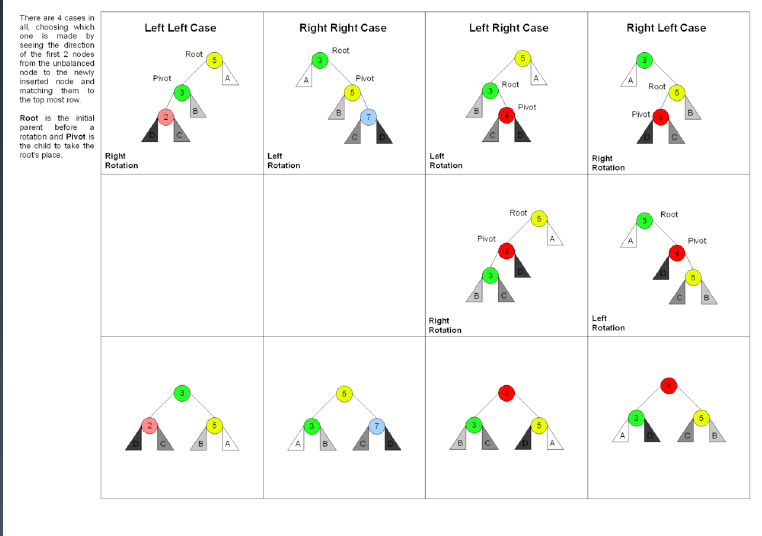
5.2 旋转操作
- 1. 左旋
- 2. 右旋
- 3. 左右旋
- 4. 右左旋
1. 左旋
2. 右旋
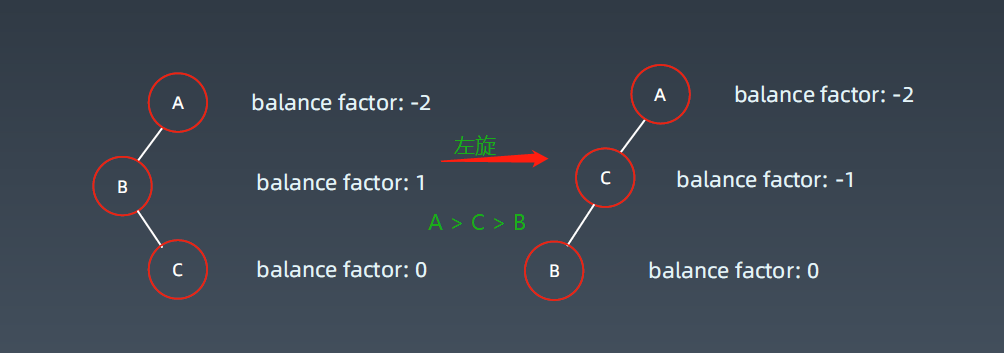
3. 左右旋
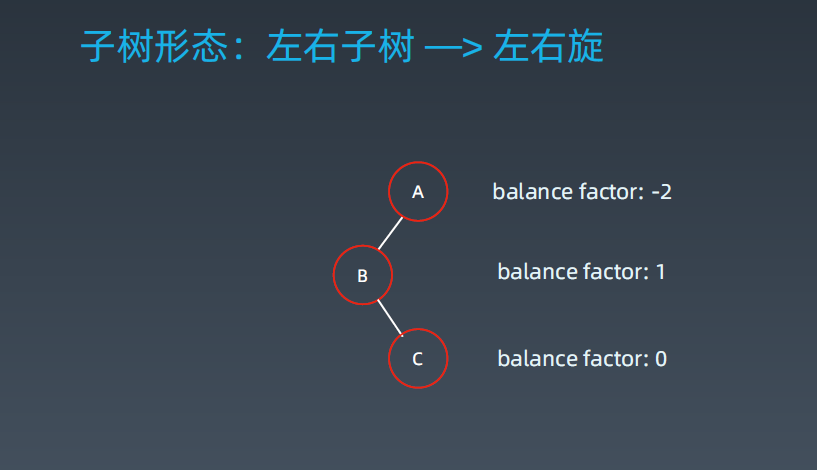
其中C > B < A，它的左旋是B拉上来，C顶上去，这样它还是符合二叉树的性质，就变成了左左子树的情况如下：
4. 右左旋
这里C < B，把它右旋上去，B挪下来，这样这个树还是满足二叉搜索树的性质
因为树的查找性能在于它的深度，记录它的左右子树深度即可，同时保证任何时候任何一个结点它的左右子树的深度差不超过绝对值1，
当它不平衡时，基础的情况是上边四种，用左右旋来维护平衡。
如果结点本身有子树的情况，它要进行左右旋和右左旋怎么办
5.3 带有子树的旋转
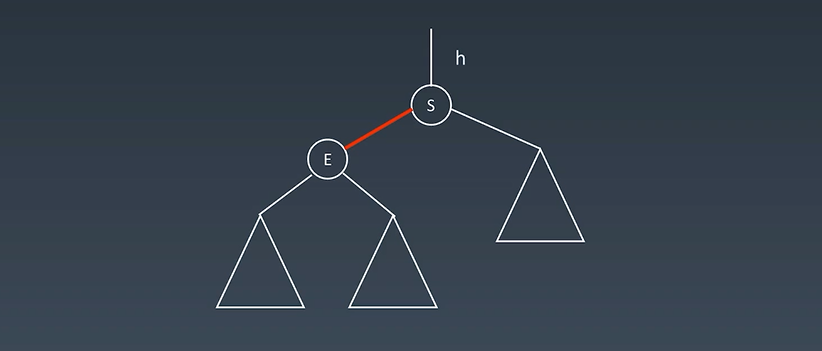
上图进行右旋操作：
E移上来，S往下之后E的右子树要挂在S的左子树去；
参考动画： https://zhuanlan.zhihu.com/p/63272157
https://en.wikipedia.org/wiki/Tree_rotation#/media/File:Tree_Rebalancing.gif
右旋：
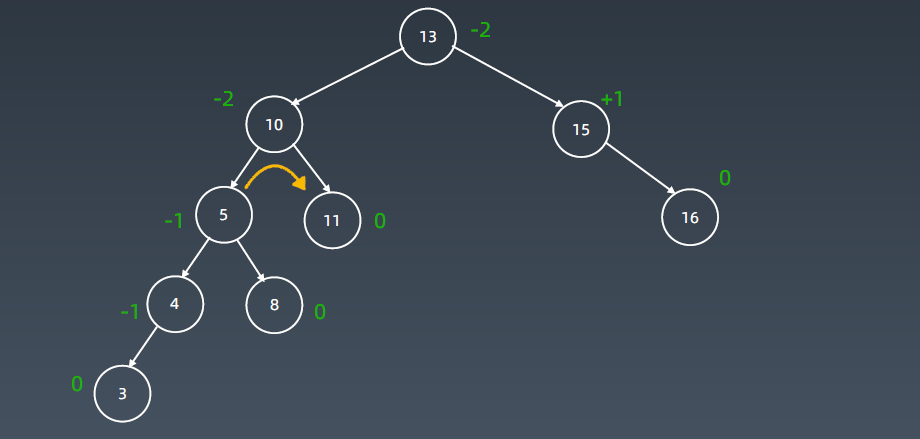
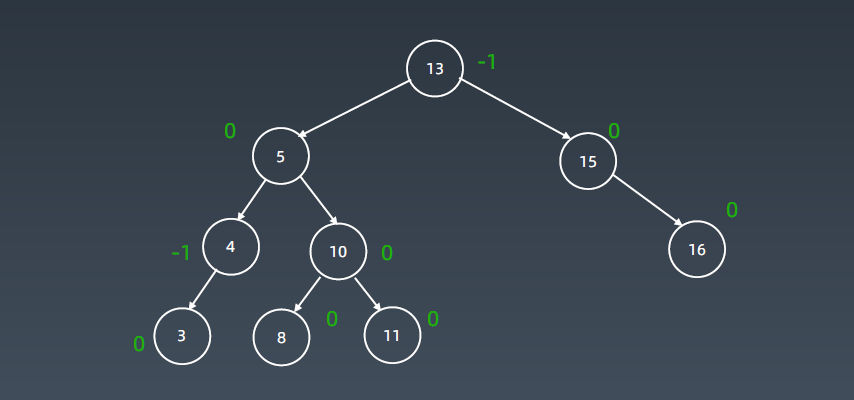
插入3后变成如上图所示树的形态。这时它就变成-2了，就变成左左型了，把5往上提10挪下去，8挪到另外一边（8挂到10的左子树上。）
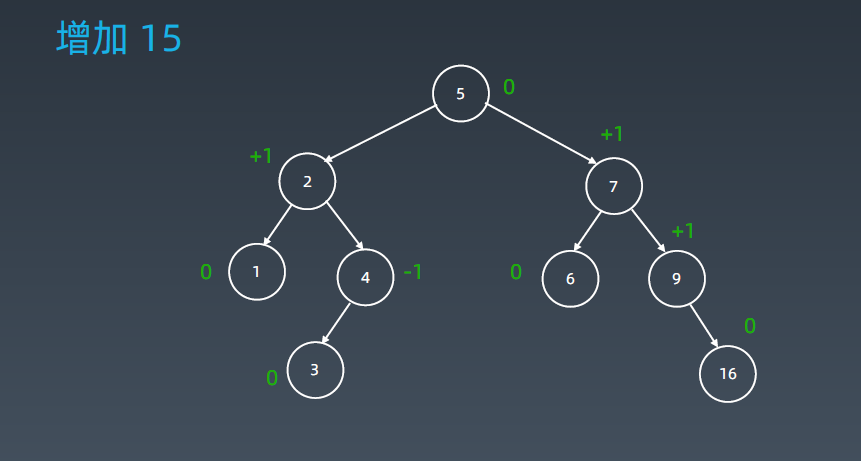
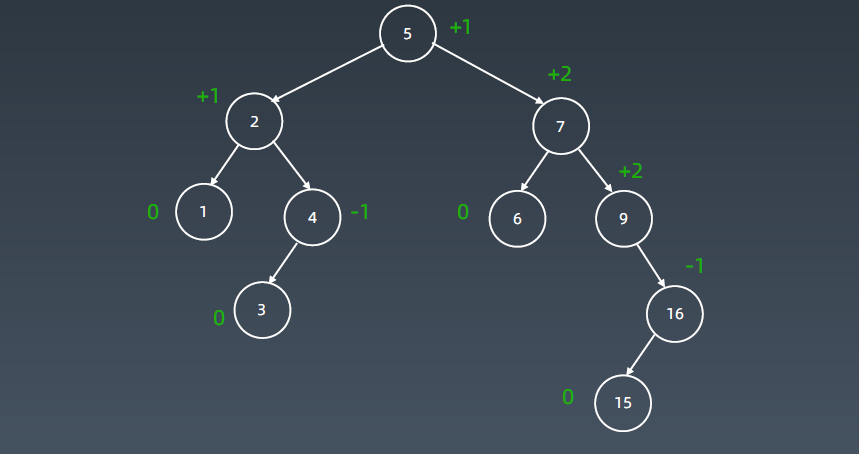
上图是典型的右左子树情况，先进行右旋再左旋。
5.4 AVL总结
1. 平衡二叉搜索树（而且是自平衡的）
2. 每个结点存 balance factor = {-1, 0, 1}
3. 四种旋转操作
不足：结点需要存储额外信息、且调整次数频繁。 （而且存储的信息是一个int类型，因为它要+-*/；频繁调整维护成本高） ==> 引入近似平衡二叉树，不需要每次非常严格的来平衡。
6. 红黑树
红黑树是一种平衡二叉查找树。是为了解决普通二叉查找树在数据更新的过程中，复杂度退化的问题而产生。红黑树的高度近似 log2n，所以它是近似平衡，插入、删除、查找操作的时间复杂度都是 O(logn)。
因为红黑树是一种性能非常稳定的二叉查找树，所以，在工程中，但凡是用到动态插入、删除、 查找数据的场景，都可以用到它。不过，它实现起来比较复杂，如果自己写代码实现，难度会有些高，这个时候，我们其实更倾向用跳表来替代它。
工程中都喜欢用红黑树这种平衡二叉查找树；红黑树“Red-Black Tree”，简称 R-B Tree，是一种不严格的平衡二叉查找树，它的定义是不严格符合平衡二叉查找树的定义的，是近似平衡二叉树的一种。
红黑树是一种近似平衡的二叉搜索树（Binary Search Tree），它能够确保任何一个结点的左右子树的高度差小于两倍。具体来说，红黑树是满足如下条件的二叉搜索树：
• 每个结点要么是红色，要么是黑色
• 根节点是黑色
• 每个叶节点（NIL节点，空节点）都是黑色的。 （每个叶子节点都是黑色的空节点（NIL），即叶子节点不存储数据，它主要是为了简化红黑树的代码实现而设置的）
• 不能有相邻接的两个红色节点。 （任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的）
• 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。（每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点；）
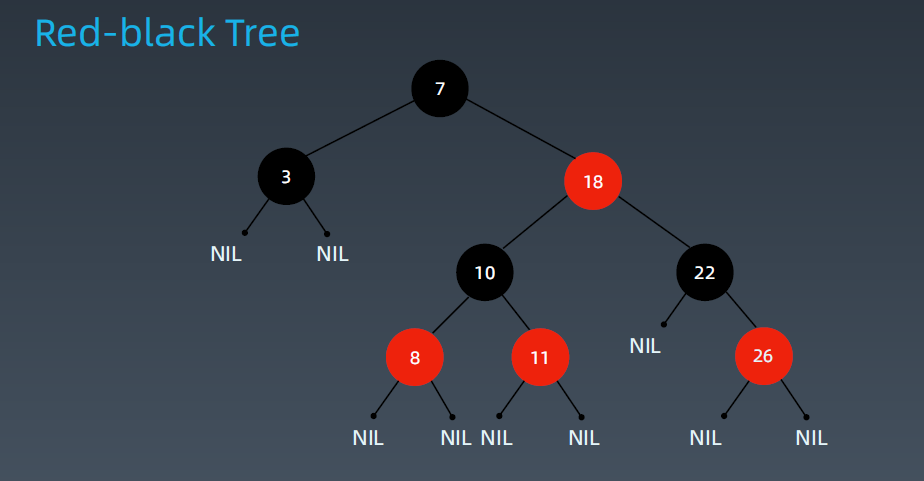
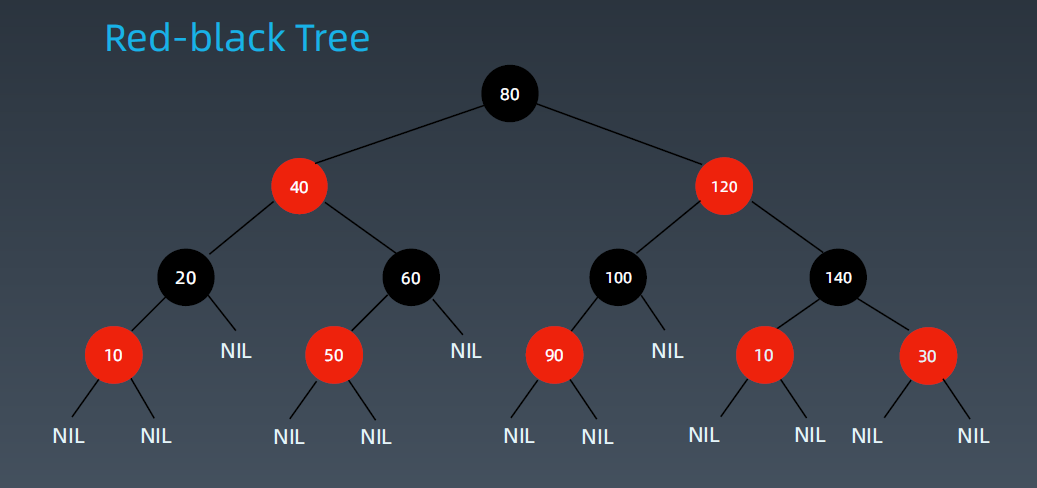
关键性质：
从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。
为什么说红黑树是“近似平衡”的？
平衡二叉查找树的初衷，是为了解决二叉查找树因为动态更新导致的性能退化问题。所以，“平衡”的意思可以等价为性能不退化。“近似平衡”就等价为性能不会退化的太严重。
红黑树的性能分析
二叉查找树很多操作的性能都跟树的高度成正比。一棵极其平衡的二叉树（满二叉树或完全二叉树）的高度大约是 log2n 。所以如果要证明红黑树是近似平衡的，只需分析红黑树的高度是否比较稳定地趋近 log2n 就好了。
将红色节点从红黑树中去掉，那单纯包含黑色节点的红黑树的高度是多少呢？
红色节点删除之后，有些节点就没有父节点了，它们会直接拿这些节点的祖父节点（父节点的父 节点）作为父节点。所以，之前的二叉树就变成了四叉树。
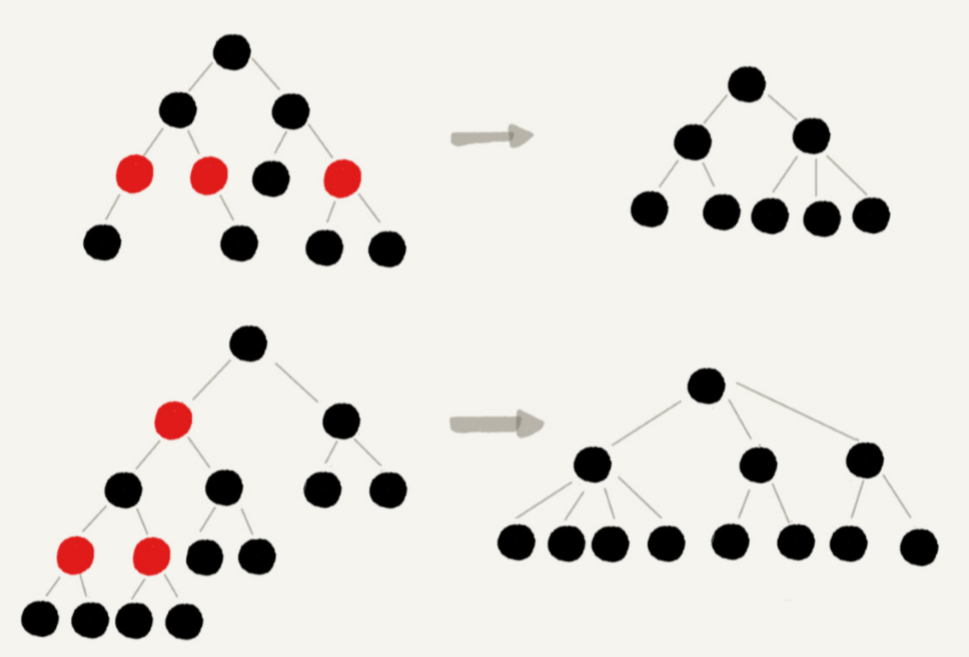
从任意节点到可达的叶子节点的每个路径包含相同数目的黑色节点。从四叉树中取出某些节点，放到叶节点位置，四叉树就变成了完全二叉树。所以，仅包含黑色节点的四叉树的高度，比包含相同节点个数的完
全二叉树的高度还要小。
完全二叉树的高度近似 log2n，这里的四叉“黑树”的高度要低于完全二叉树， 所以去掉红色节点的“黑树”的高度也不会超过 log2 n。
我们现在知道只包含黑色节点的“黑树”的高度，那现在把红色节点加回去，高度会变成多少呢？
在红黑树中，红色节点不能相邻，也就是说，有一个红色节点就要至少有一个黑色节点，将它跟其他红色节点隔开。红黑树中包含最多黑色节点的路径不会超过log2n，所以加入红色节点之后，最长路径不会超过 2log2 n，也就是说，红黑树的高度近似 2log2 n。
所以，红黑树的高度只比高度平衡的AVL 树的高度（log2 n）仅仅大了一倍，在性能上，下降得并不多。这样推导出来的结果不够精确，实际上红黑树的性能更好。
AVL和红黑树的对比
• AVL trees provide faster lookups than Red Black Trees because they are more strictly balanced.
• Red Black Trees provide faster insertion and removal operations than AVL trees as fewer rotations are done due to relatively relaxed balancing.
• AVL trees store balance factors or heights with each node, thus requires storage for an integer per node whereas Red Black Tree requires only 1 bit of information per node.
• Red Black Trees are used in most of the language libraries like map, multimap, multisetin C++ whereas AVL trees are used in databases where faster retrievals are required.
map、set全部是红黑树
DB中用AVL，读多
为什么在工程中大家都喜欢用红黑树这种平衡二叉查找树
提到的 Treap、Splay Tree，大部分情况，它们操作的效率都很高，但是也无法避免极端情况下时间复杂度的退化。尽管这种情况出现的概率不大，但是对于单次操作时间非常敏感的场景来说，它们并不适用。
AVL 树是一种高度平衡的二叉树，所以查找的效率非常高，但是，有利就有弊，AVL 树为了维持这种高度的平衡，就要付出更多的代价。每次插入、删除都要做调整，就比较复杂、耗时。所 以，对于有频繁的
插入、删除操作的数据集合，使用 AVL 树的代价就有点高了。
红黑树只是做到了近似平衡，并不是严格的平衡，所以在维护平衡的成本上，要比 AVL 树要低。
所以，红黑树的插入、删除、查找各种操作性能都比较稳定。对于工程应用来说，要面对各种异常情况，为了支撑这种工业级的应用，更倾向于这种性能稳定的平衡二叉查找树。
动态数据结构是支持动态的更新操作，里面存储的数据是时刻在变化的，通俗一点讲，它不仅支持查询，还支持删除、插入数据。而且，这些操作都非常高效。如果不高效，也就算不上是有效的动态数据结构
了。所以，这里的红黑树算一个，支持动态的插入、删除、查 找，而且效率都很高。链表、队列、栈实际上算不上，因为操作非常有限，
