算法-10 | 位运算

 

1. 二进制计数法

机器里的数字表示方式和存储格式就是 二进制

 十进制 < — > 二进制 : 如何转换？

　　4(d): 0100  （0*2^0 + 0*2^1 + 1*2^2）
　　8(d): 01000
　　5(d): 0101
　　6(d): 0110

2. 二进制的位操作-位运算

位运算符： 

左移（分为逻辑左移和计算机左移）

下图是以计算机左移，以4位为例，现在计算机大多都是64位。

　　常见的二进制位操作包括向左移位和向右移位的移位操作，以及“或”“与”“异或”的逻辑操作。

2.1 向左移位

    二进制 110101 向左移一位，就是在末尾添加一位 0，因此 110101 就变成了 1101010。（ 110101 <<  1101010 ）

数字溢出，就是二进制数的位数超过了系统所指定的位数。目前主流的系统都支持至少 32 位的整型数字。如果进行左移操作的二进制已经超出了 32 位，左移后数字就会溢出，需要将溢出的位数去除。

二进制左移一位，其实就是将数字翻倍。

2.2 向右移位

二进制 110101 向右移一位，就是去除末尾的那一位，因此 110101 就变成了 11010（最前面的 0 可以省略） （110101 >> 11010）

二进制右移一位，就是将数字除以 2 并求整数商的操作。

移位 1 次相当于乘以或除以 2，而移位 3 次就相当于乘以或除以 8（即 2 的 3 次方）

  左移位是 <<，那右移位为什么是 >>> 而不是 >> 呢？  >> 也是右移操作。之所以有这两种表达方式，根本原因是 Java 的二进制数值中最高一位是符号位。

　　　　当符号位为 0 时，表示该数值为正数；

　　　　当符号位为 1 时，表示该数值为负数。

 

例如数字 53 的二进制为 110101，从右往左数的第 32 位是 0，表示该数是正数，通常将其省略。

       数字是 -53 呢，那么第 32 位就不是 0，而是 1。  那么这个时候向右移位，就会产生一个问题：对于符号位（特别是符号位为 1 的时候），我们是否也需要将其右移呢？

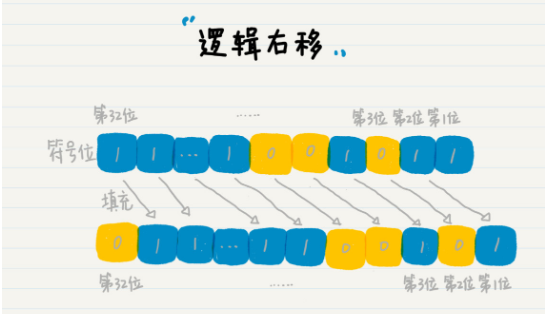
　　　　　　　　　　　　　　因此，Java 里定义了两种右移，逻辑右移 >>> 和算术右移 >> 。

• • • • • • • • • 逻辑右移>>> 1 位，左边补 0 即可，不考虑符合位。
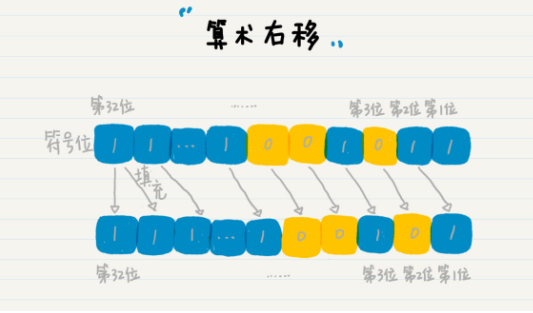
                • 算术右移>> 保持符号位不变，除符号位之外的右移一位并补符号位 1。补的 1 仍然在符号位之后。

            

2.3 位的“或”  | 

 逻辑“或”的意思是，参与操作的位中只要有一个位是 1，那么最终结果就是 1，也就是“真”。如果我们将二进制 110101 和 100011 的每一位对齐，进行按位的“或”操作，就会得到 110111。

2.4 位的“与” &

 “与”的意思是，参与操作的位中必须全都是 1，那么最终结果才是 1（真），否则就为 0（假）。如果我们将二进制 110101 和 100011 的每一位对齐，进行按位的“与”操作，就会得到 100001。

2.5 位的“异或”XOR  ^ 

       相同为0不同为1， "不进位加法"

  位的“异或”逻辑“异或”和“或”有所不同，它具有排异性，也就是说如果参与操作的位相同，那么最终结果就为 0（假），否则为 1（真）。所以，如果要得到 1，参与操作的两个位必须不同，这就是此处“异”的含义。

  我们将二进制 110101 和 100011 的每一位对齐，进行按位的“异或”操作，可以得到结果是 10110。

 “异或”操作的本质其实就是，所有数值和自身进行按位的“异或”操作之后都为 0。而且要通过“异或”操作得到 0，也必须通过两个相同的数值进行按位“异或”。这表明了两个数值按位“异或”结果为 0，是这两个数值相等的必要充分条件，可以作为判断两个变量是否相等的条件。

异或：相同为 0，不同为 1。也可用“不进位加法”来理解。
异或操作的一些特点：
x ^ 0 = x
x ^ 1s = ~x // 注意 1s = ~0 　　0s表示一串0，1s表示一串1
x ^ (~x) = 1s
x ^ x = 0
c = a ^ b => a ^ c = b, b ^ c = a // 交换两个数
a ^ b ^ c = a ^ (b ^ c) = (a ^ b) ^ c // associative

2.6 按位取反 ~

   0011 -------- =>  1100

2.7 指定位置的位运算

指定位置的位运算：
    1. 将 x 最右边的 n 位清零：x & (~0 << n)
    2. 获取 x 的第 n 位值（0 或者 1）： (x >> n) & 1
    3. 获取 x 的第 n 位的幂值：x & (1 << (n -1))
    4. 仅将第 n 位置为 1：x | (1 << n)
    5. 仅将第 n 位置为 0：x & (~ (1 << n))
    6. 将 x 最高位至第 n 位（含）清零：x & ((1 << n) - 1)
    7. 将第 n 位至第 0 位（含）清零：x & (~ ((1 << (n + 1)) - 1))

 

2.8常用的运算要点

实战运算要点：
• 判断奇偶：
    x % 2 == 1 —> (x & 1) == 1
    x % 2 == 0 —> (x & 1) == 0
• x >> 1 —> x / 2
    即： x = x / 2; —> x = x >> 1;
         mid = (left + right) / 2; —> mid = (left + right) >> 1;

• X = X & (X-1) =>      二进制清零最低位的 1，  X & (X-1) 结果不是 X - 1 
• X & -X        => 1　　 得到最低位的 1
• X & ~X        => 0

3. 位运算的应用

 N皇后的位运算解法

python

def totalNQueens(self, n):
    if n < 1: return []
    self.count = 0
    self.DFS(n, 0, 0, 0, 0)
    return self.count
def DFS(self, n, row, cols, pie, na):
    # recursion terminator
    if row >= n:
        self.count += 1
        return
    bits = (~(cols | pie | na)) & ((1 << n) — 1) # 得到当前所有的空位
    while bits:
        p = bits & —bits # 取到最低位的1
        bits = bits & (bits — 1) # 表示在p位置上放⼊皇后
        self.DFS(n, row + 1, cols | p, (pie | p) << 1, (na | p) >> 1)
        # 不需要revert cols, pie, na 的状态    

Java

class Solution {
    private int size;
    private int count;
    private void solve(int row, int ld, int rd) {
        if (row == size) {
        count++;
        return;
        }
        int pos = size & (~(row | ld | rd));
        while (pos != 0) {
            int p = pos & (-pos);
            pos -= p; // pos &= pos - 1;
            solve(row | p, (ld | p) << 1, (rd | p) >> 1);
            }
        }
        public int totalNQueens(int n) {
            count = 0;
            size = (1 << n) - 1;
            solve(0, 0, 0);
            return count;
    }
}