数据结构-05| BitMap位图 |布隆过滤器
位图 BitMap
存储结构，位图（BitMap）。布隆过滤器本身就是基于位图的，是对位图的一种改进。
有 1 千万个整数，整数的范 围在 1 到 1 亿之间。如何快速查找某个整数是否在这 1 千万个整数中？
当然，这个问题还是可以用散列表来解决。不过，我们可以使用一种比较“特殊”的散列表，那就是位图。我们申请一个大小为 1 亿、数据类型为布尔类型（true 或者 false）的数组。将这 1 千万个整数作为数组
下标，将对应的数组值设置成 true。比如，整数 5 对应下标为 5 的数组值设置为 true，也就是 array[5]=true。
当查询某个整数 K 是否在这 1 千万个整数中时，只需要将对应的数组值 array[K] 取出来，看是否等于 true。如果等于 true，那说明 1 千万整数中包含这个整数 K；相反，就表示不包含这个整数 K。
不过很多语言中提供的布尔类型，大小是 1 个字节，并不能节省太多内存空间。实际上，表示 true 和 false 两个值，只需用一个二进制位（bit）就可以了。那如何通过编程语言，来表示一个二进制位呢？
这里就要用到位运算了。我们可以借助编程语言中提供的数据类型，比如 int、long、char 等类型，通过位运算，用其中的某个位表示某个数字。位图的代码如下：
public class BitMap { // System.out.println(Character.SIZE); //结果16 Java中char类型占16bit，也即是2个字节
private char[] bytes;
private int nbits;
public BitMap(int nbits) {
this.nbits = nbits;
this.bytes = new char[nbits / 16 + 1];
}
public void set(int k) {
if (k > nbits) return;
int byteIndex = k / 16;
int bitIndex = k % 16;
bytes[byteIndex] |= (1 << bitIndex);
}
public boolean get(int k) {
if (k > nbits) return false;
int byteIndex = k / 16;
int bitIndex = k % 16;
return (bytes[byteIndex] & (1 << bitIndex)) != 0;
}
}
位图通过数组下标来定位数据，所以，访问效率非常高。而且，每个数字用一个二进制位来表示，在数字范围不大的情况下，所需要的内存空间非常节省。
这里有个假设，就是数字所在的范围不是很大。如果数字的范围很大，数字范围不是 1 到 1 亿，而是 1 到 10 亿，那位图的大小就是 10 亿个二进制位，也就是120MB 的大小，消耗的内存空间，不降反增。
这时布隆过滤器就要出场了。布隆过滤器就是为了解决刚刚这个问题，对位图这种数据结构的一种改进。
布隆过滤器 Bloom Filter
还是那个例子，数据个数是 1 千万，数据的范围是 1 到 10 亿。布隆过滤器的做法是，仍然使用一个 1 亿个二进制大小的位图，然后通过哈希函数，对数字进行处理，让它落在这 1 到 1 亿范围内。比如我们
把哈希函数设计成 f(x)=x%n。其中，x 表示数字，n 表示位图的大小 （1 亿），也就是，对数字跟位图的大小进行取模求余。
哈希函数会存在冲突的问题啊，一亿零一和 1 两个数字，经过刚刚那个取模求余的哈希函数处理之后，最后的结果都是 1。这样就无法区分，位图存储的是 1 还是一亿零一了。
为了降低这种冲突概率，可以设计一个复杂点、随机点的哈希函数。除此之外，还有其他方法吗？参看布隆过滤器的处理方法。既然一个哈希函数可能会存在冲突，那用多个哈希函数一块儿定位一个数据，是否能降低冲突的概率呢？布隆过滤器是怎么做的。
我们使用 K 个哈希函数，对同一个数字进行求哈希值，会得到 K 个不同的哈希值，分别记作 $X_{1}$，$X_{2}$，$X_{3}$，…，$X_{K}$。把这 K 个数字作为位图中的下标，将对应的
BitMap[$X_{1}$]，BitMap[$X_{2}$]，BitMap[$X_{3}$]，…，BitMap[$X_{K}$] 都设置成 true，也就是说，用 K 个二进制位，来表示一个数字的存在。
当要查询某个数字是否存在的时候，用同样的 K 个哈希函数，对这个数字求哈希值， 分别得到 $Y_{1}$，$Y_{2}$，$Y_{3}$，…，$Y_{K}$。我们看这 K 个哈希值，对应位图中的数 值是否都为 true，
如果都是 true，则说明，这个数字存在，如果有其中任意一个不为 true，就说明这个数字不存在。
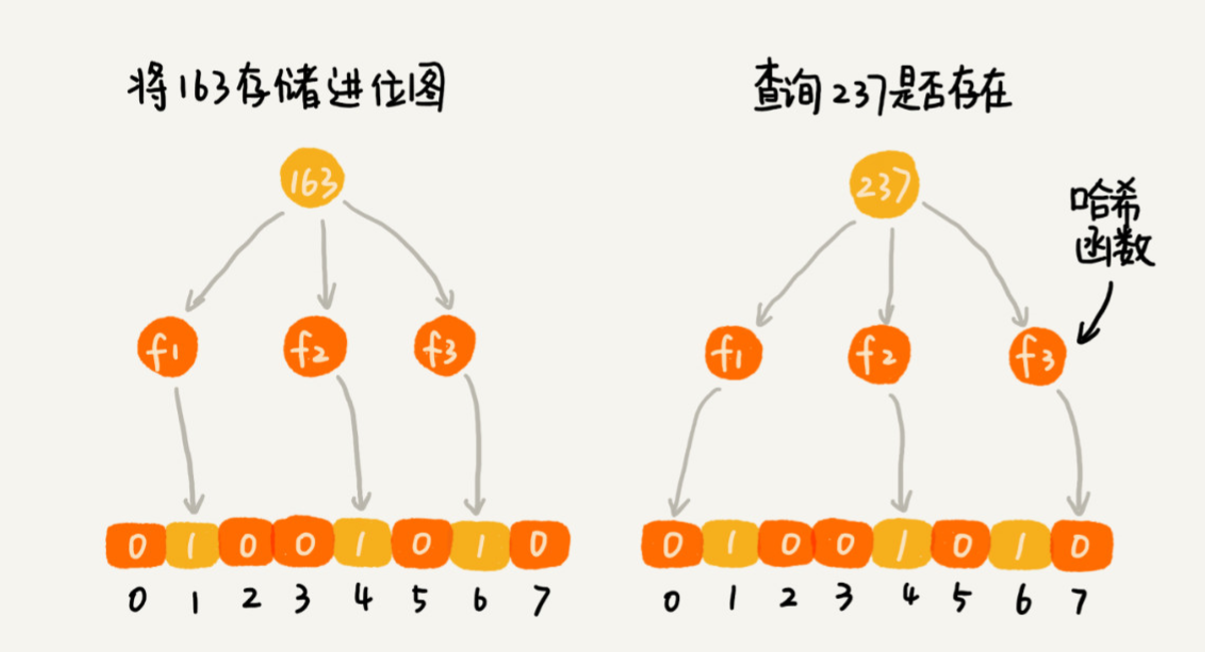
对于两个不同的数字来说，经过一个哈希函数处理之后，可能会产生相同的哈希值。但是经过 K 个哈希函数处理之后，K 个哈希值都相同的概率就非常低了。尽管采用 K 个哈希函数之后，两个数字哈希冲突的
概率降低了，但这种处理方式又带来了新的问题，那就是容易误判。
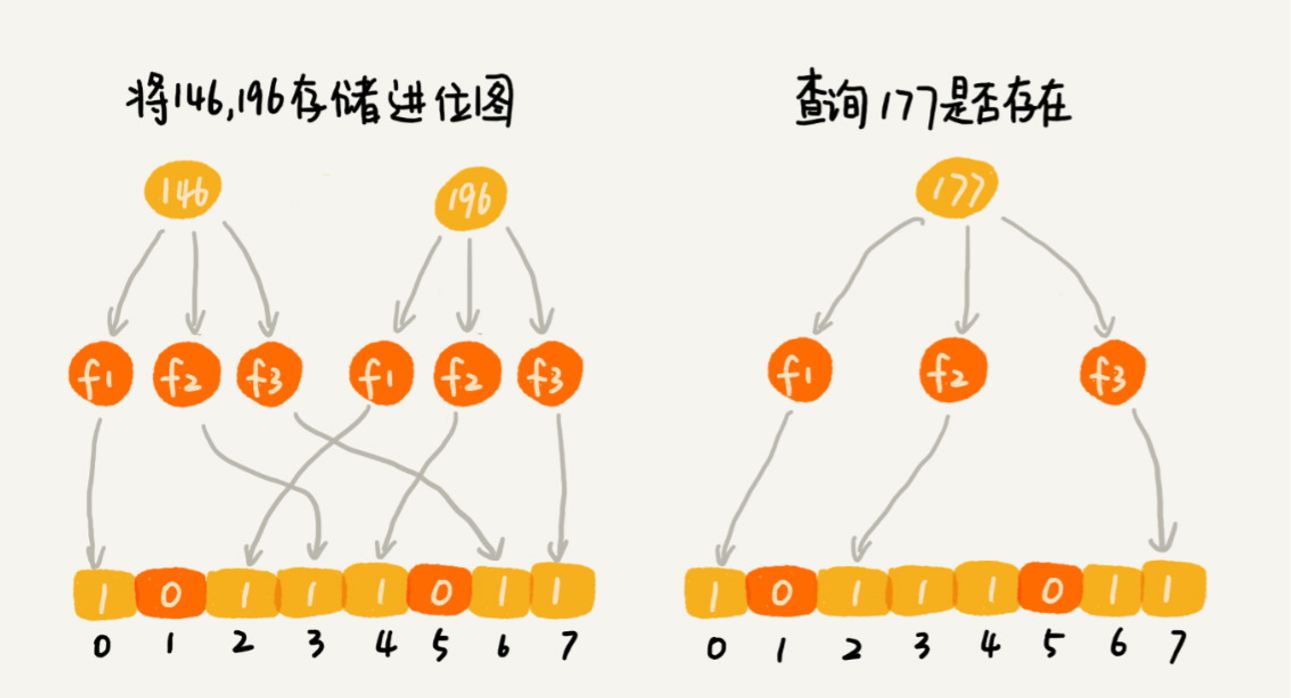
布隆过滤器的误判有一个特点，那就是，它只会对存在的情况有误判。如果某个数字经过布隆过滤器判断不存在，那说明这个数字真的不存在，不会发生误判；
如果某个数字经过布隆过滤器判断存在，这时才会有可能误判，有可能并不存在。
不过，只要我们调整哈希函数的个数、位图大小跟要存储数字的个数之间的比例，那就可以将这种误判的概率降到非常低。
尽管布隆过滤器会存在误判，但是，这并不影响它发挥大作用。很多场景对误判有一定的容忍度。比如爬虫判重这个问题，即便一个没有被爬取过的网页，被误判为已经被爬取，对于搜索引擎来说，也并不是什
么大事情，是可以容忍的，毕竟网页太多了，搜索引擎也 不可能 100% 都爬取到。
布隆过滤器和哈希表类似，HashTable + 拉链表存储重复元素：
元素 ---哈希函数---> 映射到一个整数的下标位置index。比如Join Smith和Sandra Dee经过哈希函数都映射到了152的下标，就在152的位置开一个链表，把多个元素都存在相同位置的链表处，往后边不断的积累积累。
它不仅有哈希函数得到一个index值，且会把整个要素的元素都存储到哈希表里边去，这是一个没有误差的数据结构，有多少个元素，每个元素有多大，所有这些元素所占的内存空间等在哈希表里边都要有相应的内存大小给存储起来。
但是在很多工业级应用中，我们并不需要存储所有的元素本身，而只需要存储一个信息，即这个元素在这个表里边有没有，这时就需要更高效的一种数据结构。
Bloom Filter VS HashTable
布隆过滤器即 一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否存在一个集合中。（而哈希表不只是判断元素是否在一个集合中，同时还可以存元素本身和元素的各种额外信息。布隆过滤器只用于检索一个元素它是否在还是不在的信息，而不能存其它的额外信息）
优点：空间效率和查询时间都远远超过一般的算法，
缺点是有一定的误识别率和删除困难。
布隆过滤器示意图：
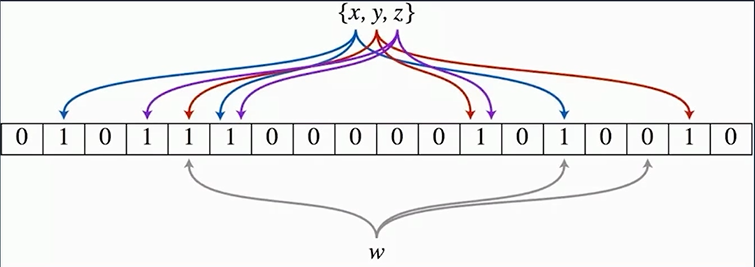
x,y,z不是同时往里边添加,一个一个的添加; 每一个元素它会分配到一系列的二进制位中。
假设x会分配3个二进制位,蓝色线表示, 把x插入布隆过滤器时即把x对应的这三个位置置为1就可以了。
y插入进来,根据它的哈希函数分为红色的这三条线所对应的二进制位,置为1。
同理z也置为1。
这个二进制的数组用来表示所有的已经存入的xyz是否已经在索引里边了。
重新插入一个x, 这时x始终会对应这3个蓝色的二进制位, 去表里查就查到这三个都是1, 所以我们认为x是存在的。
如果是一个陌生的元素w进来, 它把它分配给通过布隆过滤器的二进制索引的函数, w就得到灰色的这三个二进制位110, 有一个为0说明w未在索引里边。
只要布隆过滤器中有一个为0就说明这个元素不在布隆过滤器的索引里面, 且我们肯定它不在。
但比如又来一个元素q, 它刚好分配的三个二进制都为1, 我们不一定说它是存在的。
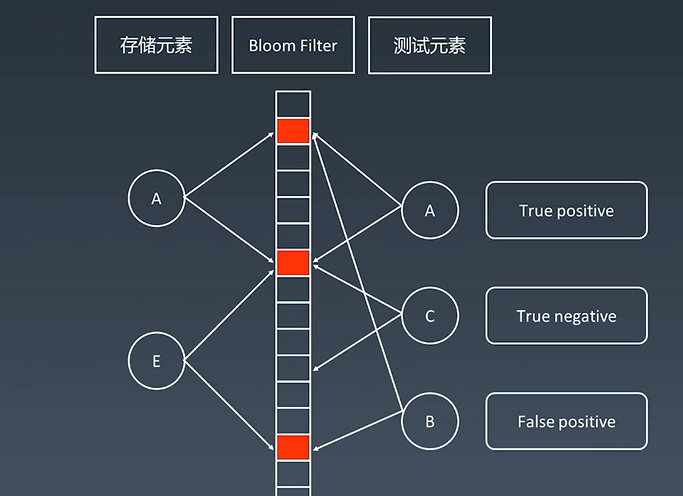
存储元素A和E都存入布隆过滤器中，置为1.
测试元素，A查到到它的二进制位为1，可能是有的；C查到它的二进制位有一个为0，则C肯定不在布隆过滤器里边；B恰好分配的二进制位都为1，但从来没有存储过B，则我们会判断B在这个索引里边，这个时候对于B的判断就是有误差的。
结论：
当布隆过滤器把元素全部插入完之后, 对于测试(新来)的元素要验证它是否存在
当它验证这个元素所对应的二进制位是1时, 我们只能说它可能存在布隆过滤器里边。
但是当这个元素所对应的二进制位只要有一个不为1, 则它肯定不在。
---一个元素去布隆过滤器里边查, 如果查到它不存在, 那么它肯定就是不存在的。
如果查到它的二进制都是1,为存在的状态比如B,则它可能存在。
那我们到底怎么判断B这种元素是否存在呢?
布隆过滤器只是放在外边当一个缓存使用，来作为一个很快速的判断来使用
当B查到了，布隆过滤器里边是存在的，则B会继续在这个机器上的数据库DB中来查询，去查询B是否存在。
而C就会直接打到布隆过滤器里边，这样C就不用查询了节省了查询访问数据库的时间。
布隆过滤器只是挡在一台机器前边的快速查询的缓存。
案例
①.比特币网络
②.分布式系统(Map-Reduce) -- Hadoop、 Searchengine
③.Redis缓存
④.垃圾邮件、评论等的过滤
https://www.cnblogs.com/cpselvis/p/6265825.html
https://blog.csdn.net/tianyaleixiaowu/article/details/74721877
布隆过滤器的Java代码实现：
https://github.com/lovasoa/bloomfilter/blob/master/src/main/java/BloomFilter.java
https://github.com/Baqend/Orestes-Bloomfilter
应用
网页爬虫是搜索引擎中的非常重要的系统，负责爬取几十亿、上百亿的网页。爬虫的工作原理 是，通过解析已经爬取页面中的网页链接，然后再爬取这些链接对应的网页。而同一个网页链接 有可能被包含在多
个页面中，这就会导致爬虫在爬取的过程中，重复爬取相同的网页。如何避免这些重复的爬取 ？
最容易想到的方法就是，记录已经爬取的网页链接（也就是 URL），在爬取一个新的网页 之前，拿它的链接，在已经爬取的网页链接列表中搜索。
如果存在，那就说明这个网页已经被爬取过了；如果不存在，那就说明这个网页还没有被爬取过，可以继续去爬取。等爬取到这个 网页之后，我们将这个网页的链接添加到已经爬取的网页链接列表了。
思路非常简单，该如何记录已经爬取的网页链接呢？要用什么样的数据结构
这个问题要处理的对象是网页链接，也就是 URL，需要支持的操作有两个，添加一个 URL 和查询一个 URL。除了这两个功能性的要求之外，在非功能性方面，还要求这两个操作的执行 效率要尽可能高。除此之外，因为处理的是上亿的网页链接，内存消耗会非常大，所以在存储效率上，要尽可能地高效。
满足这些条件的数据结构有散列表、红黑树、跳表这些动态数据 结构，都能支持快速地插入、查找数据，但是对内存消耗方面，是否可以接受呢？
以散列表为例：
假设我们要爬取 10 亿个网页（像 Google、百度这样的通用搜索引擎， 爬取的网页可能会更多），为了判重，把这 10 亿网页链接存储在散列表中。估算下大约需要的内存：
假设一个 URL 的平均长度是 64 字节，那单纯存储这 10 亿个 URL，需要大约 60GB 的内存空 间。因为散列表必须维持较小的装载因子，才能保证不会出现过多的散列冲突，导致操作的性能 下降。而且，用链
表法解决冲突的散列表，还会存储链表指针。所以，如果将这 10 亿个 URL 构建成散列表，那需要的内存空间会远大于 60GB，有可能会超过 100GB。
当然，对于一个大型的搜索引擎来说，即便是 100GB 的内存要求，其实也不算太高，我们可以采用分治的思想，用多台机器（比如 20 台内存是 8GB 的机器）来存储这 10 亿网页链接。
对于爬虫的 URL去重这个问题，刚刚讲到的分治加散列表的思路，已经是可以实实在在工作的 了。
不过，作为一个有追求的工程师，我们应该考虑，在添加、查询数据的效率以及内存消耗方 面，我们是否还有进一步的优化空间呢？
散列表中添加、查找数据的时间复杂度已经是 O(1)，还能有进一步优化的空间吗？实际上，时间复杂度并不能完全代表代码的执行时间。大 O 时间复杂度表示法，会忽略掉常数、系数和低阶，并且统计的对象
是语句的频度。不同的语句，执行时间也 是不同的。时间复杂度只是表示执行时间随数据规模的变化趋势，并不能度量在特定的数据规模 下，代码执行时间的多少。
如果时间复杂度中原来的系数是 10，能够通过优化，将系数降为 1，那在时间复杂度没有变化的情况下，执行效率就提高了 10 倍。对于实际的软件开发来说，10 倍效率的提升， 显然是一个非常值得的优化。
如果我们用基于链表的方法解决冲突问题，散列表中存储的是 URL，那当查询的时候，通过哈希函数定位到某个链表之后，还需要依次比对每个链表中的 URL。这个操作比较耗时，主要有两点原因。
一方面，链表中的结点在内存中不是连续存储的，所以不能一下子加载到 CPU 缓存中，没法很好地利用到 CPU 高速缓存，所以数据访问性能方面会打折扣
另一方面，链表中的每个数据都是 URL，而 URL 不是简单的数字，是平均长度为 64 字节的字 符串。也就是说，我们要让待判重的 URL，跟链表中的每个 URL，做字符串匹配。显然，这样 一个字符串匹配操
作，比起单纯的数字比对，要慢很多。所以，基于这两点，执行效率方面肯定 是有优化空间的。
对于内存消耗方面的优化，除了刚刚这种基于散列表的解决方案。实际 上，如果要想内存方面有明显的节省，那就得换一种解决方案，使用布隆过滤器（Bloom Filter）这种数据结构。
如果用散列表存储这 1 千万的数据，数据是 32 位的整型数，也就是需要 4 个字节的存储空间，那总共至少需要 40MB 的存储空间。如果通过位图的话，数字范围在 1 到 1 亿之间，只
需要 1 亿个二进制位，也就是 12MB 左右的存储空间就够了。
布隆过滤器
我们用布隆过滤器来记录已经爬取过的网页链接，假设需要判重的网页有 10 亿，那我们可以用 一个 10 倍大小的位图来存储，也就是 100 亿个二进制位，换算成字节，那就是大约 1.2GB。 之前用散列表判重，
需要至少 100GB 的空间。相比来讲，布隆过滤器在存储空间的消耗上，降低了非常多。
利用布隆过滤器，在执行效率方面，是否比散列表更加高效呢？
布隆过滤器用多个哈希函数对同一个网页链接进行处理，CPU 只需要将网页链接从内存中读取 一次，进行多次哈希计算，理论上讲这组操作是 CPU 密集型的。而在散列表的处理方式中，需要读取散列冲突拉
链的多个网页链接，分别跟待判重的网页链接，进行字符串匹配。这个操作涉 及很多内存数据的读取，所以是内存密集型的。我们知道 CPU 计算可能是要比内存访问更快速 的，所以，理论上讲，布隆过滤器的
判重方式，更加快速。
总结
关于搜索引擎爬虫网页去重问题的解决，从散列表讲到位图，再到布隆过滤器。 隆过滤器非常适合这种不需要 100% 准确的、允许存在小概率误判的大规模判重场景。
除了爬虫网页去重这个例子，还有比如统计一个大型网站的每天的 UV 数，也就是每天有多少用户访问了网站，我们就可以使用布隆过滤器，对重复访问的用户，进行去重。
布隆过滤器的误判率，主要跟哈希函数的个数、位图的大小有关。当我们往布隆 过滤器中不停地加入数据之后，位图中不是 true 的位置就越来越少了，误判率就越来越高了。 所以，对于无法事先知道要判重的
数据个数的情况，我们需要支持自动扩容的功能。
当布隆过滤器中，数据个数与位图大小的比例超过某个阈值的时候，就重新申请一个新的位图。后面来的新数据，会被放置到新的位图中。但是，如果我们要判断某个数据是否在布隆过滤 器中已经存在，我们
就需要查看多个位图，相应的执行效率就降低了一些。
位图、布隆过滤器应用如此广泛，很多编程语言都已经实现了。比如 Java 中的 BitSet 类就是一 个位图，Redis 也提供了 BitMap 位图类，Google 的 Guava 工具包提供了 BloomFilter 布隆 过滤器的实现。
1. 假设我们有 1 亿个整数，数据范围是从 1 到 10 亿，如何快速并且省内存地给这 1 亿个数 据从小到大排序？
传统的做法：1亿个整数，存储需要400M空间，排序时间复杂度最优 N×log(N)
使用位图算法：数字范围是1到10亿，用位图存储120M（10亿 / 8 / 1024 / 1024）就够了，然后将1亿个数字依次添加到位图中，然后再将位图按下标从小到大输出值为1的下标，排序就完成了，时间复杂度为 N
要把这一亿个整数排序，最简单的做法，把这1亿个整数存到位图中，位图大小是10亿bit，约120MB，位图中位的顺序即为整数的顺序。
数字重复了， 对于重复的可以再维护一个小的散列表记录出现次数超过1次的数据以及对应的个数。
Bloom filter删除数据时，不能把bit位置0，解决方案， 一般不用来删除，如果非要支持删除，可以再弄个数据结构记录删除的数据。
2. 还记得我们在哈希函数（下）的利用分治思想，用散列表以及哈希函数，实现海量图库中的判重功能吗？如果我们允许小概率的误判，那是否可以用今天的布隆过滤器来解决呢？ 参照当时的估算方法，重新
估算下，用布隆过滤器需要多少台机器？
如果采用布隆过滤器，可以用10亿bit位存储1亿图片的信息(包括图片唯一标识和图片文件路径长)，10亿bit约为120MB, 如果单机的内存容量上限为2GB，那么只需要1台机器就可以存贮。
