算法-04| 贪心算法

1. Greedy

贪心算法（greedy algorithm）。贪心算法有很多经典的应用，比如霍夫曼编码（Huffman Coding）、Prim 和 Kruskal 最小生成树算法、还有 Dijkstra 单源最短路径算法。最小生成树算法和最短路径算法，

霍夫曼编码，看看它是如何利用贪心算法来实现对数据压缩编码，有效节省数据存储空间的。

 

贪心算法是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是全局最好或最优的算法。

 

2. 贪心算法与回溯和动态规划

贪心算法与动态规划的不同点：

贪心算法与动态规划的不同在于它对每个子问题的解决方案都做出选择，不能回退。

动态规划则会保存以前的运算结果，并根据以前的结果对当前进行 选择，有回退功能。

    贪心：当下做局部最优判断，同时是不能回退的；

    回溯：能够回退；

   动态规划：最优判断 + 回退；（带有最优判断的回溯就是动态规划）

3. 适用情景

    简单地说，问题能够分解成子问题来解决，子问题的最优解能递推到最终 问题的最优解。这种子问题最优解称为最优子结构。

贪心算法与动态规划的不同在于它对每个子问题的解决方案都做出选择， 不能回退。动态规划则会保存以前的运算结果，并根据以前的结果对当前 进行选择，有回退功能。

     贪心法可以解决一些最优化问题，选最优选最近选最好都可以用贪心算法，如：求图中的最小生成树、求哈夫曼编码 等。然而对于工程和生活中的问题，贪心法一般不能得到我们所要求的答案（选择眼前最优，一般来说达不到全局最优）。

     一旦一个问题可以通过贪心法来解决，那么贪心法一般是解决这个问题的最 好办法。由于贪心法的高效性以及其所求得的答案比较接近最优结果，贪心 法也可以用作辅助算法或者直接解决一些要求结果不特别精确的问题。

4. 案例

4.1 Coin Change钱币找零案例

Coin Change 使用贪心算法的特例

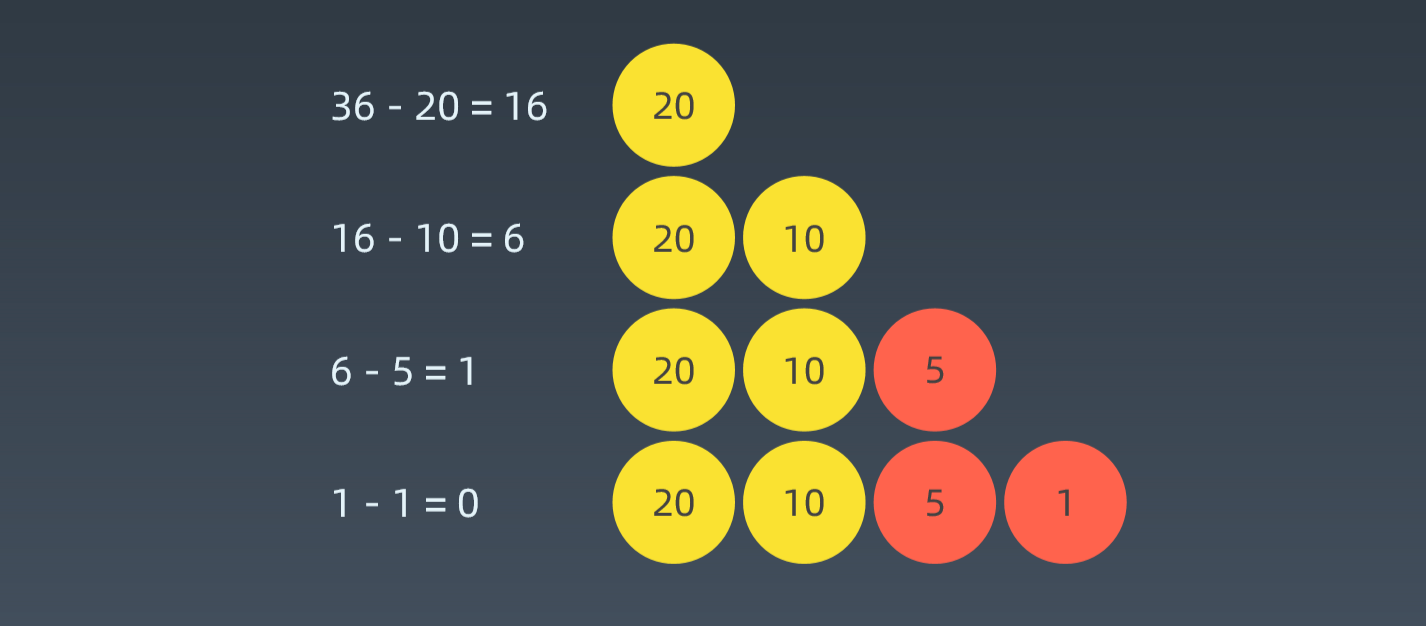
当硬币可选集合固定：Coins = [20, 10, 5, 1]

　　求最少可以几个硬币拼出总数。 比如 total = 36

      首先用20去匹配（36/20 整数个20）36 - 20 = 16， 再用6去匹配（16 / 10 整数个10）16 - 10 = 6， 再用5匹配，最后用1匹配得到 36.

这种特殊情况是，前面这些硬币依次是后面这些硬币的倍数（这些硬币20，10, 5， 1有整除关系），可以从数学上证明贪心法每次用最大的即可。这种特殊情况下，贪心算法是成立的。

Coin Change使用贪心算法的反例

非整除关系的硬币，可选集合：Coins = [10, 9, 1] 

　　求拼出总数为 18 最少需要几个硬币 ？最优化的方案是两个9， 使用贪心算法的结果是10, 1, 1, 1, 1, 1, 1, 1, 1 ，其结果并不是最优的。

　　18 - 9 = 9；

　 　9 - 9 = 0；

 

找零问题在生活中，肯定是先用面值最大的来支付，如果不够，就继续用更小一点面值的，以此类推，最后剩下的用 1 元来补齐。

在贡献相同期望值（纸币数目）的情况下，希望多贡献点金额，这样就可以让纸币数更少，这就是一种贪心算法的解决思路。直觉告诉我们，这种处理方法就是最好的。

     但找零问题不能用贪婪算法，比如币值为100，99和1的3种币种，每种各一百张，找396元。 动态规划可求出四张99元，但贪心算法解出需三张一百和96张一元。

 

4.2 背包

有一个可以容纳 100kg 物品的背包，可以装各种物品。有 5 种豆子，每种豆子的总量和总价值都各不相同。为了让背包中所装物品的总价值最大，如何选择在背包中装哪些豆子？每种豆子又该装多少？

  

 

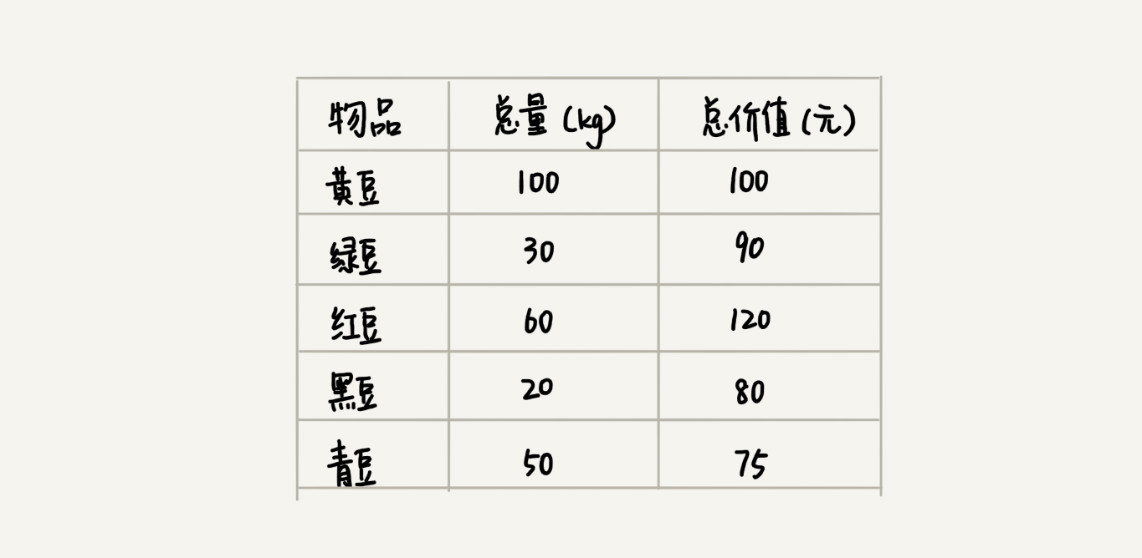
 先算一算每个物品的单价，按照单价由高到低依次来装就好了。单价（元 / kg）从高到低排列，依次是：黑豆（4）、绿豆（3）、红豆（2）、青豆（1.5）、黄豆（1），所以，我们可以往背包里装 20kg 黑豆、30kg 绿豆、50kg 红豆。它本质上借助的就是贪心算法。

贪心算法解决问题的步骤：

第一步，看到这类问题的时候，首先要联想到贪心算法：针对一组数据，定义了限制值和期望值，希望从中选出几个数据，在满足限制值的情况下，期望值最大。

　　类比到刚刚的例子，限制值就是重量不能超过 100kg，期望值就是物品的总价值。这组数据就是 5 种豆子。我们从中选出一部分，满足重量不超过 100kg，并且总价值最大。

第二步，尝试看下这个问题是否可以用贪心算法解决：每次选择当前情况下，在对限制值同等贡献量的情况下，对期望值贡献最大的数据。

　　类比到刚刚的例子，每次都从剩下的豆子里面，选择单价最高的，也就是重量相同的情况下，对价值贡献最大的豆子。

第三步，举几个例子看下贪心算法产生的结果是否是最优的。大部分情况下，举几个例子验证一下就可以。严格地证明贪心算法的正确性，需要涉及比较多的数学推理。且从实践的角度，大部分能用贪心算法解决的问题，贪心算法的正确性都是显而易见的，也不需要严格的数学推导证明。

 

4.3 分糖果

有 m 个糖果和 n 个孩子。要把糖果分给孩子吃，但是糖果少，孩子多（m < n），所以糖果只能分配给一部分孩子。

每个糖果的大小不等，这 m 个糖果的大小分别是 s1，s2，s3，……，sm。除此之外，每个孩子对糖果大小的需求也是不一样的，只有糖果的大小大于等于孩子的对糖果大小的需求时，孩子才得到满足。假设这 n 个孩子对糖果大小的需求分别是 g1，g2，g3，……，gn。

如何分配糖果，能尽可能满足最多数量的孩子？

可把这个问题抽象成，从 n 个孩子中，抽取一部分孩子分配糖果，让满足的孩子的个数（期望值）是最大的。这个问题的限制值就是糖果个数 m。

利用贪心算法，对于一个孩子来说，如果小的糖果可以满足，就没必要用更大的糖果，这样更大的就可以留给其他对糖果大小需求更大的孩子。

　　　　　 　另一方面，对糖果大小需求小的孩子更容易被满足，所以，可以从需求小的孩子开始分配糖果。因为满足一个需求大的孩子跟满足一个需求小的孩子，对我们期望值的贡献是一样的。

每次从剩下的孩子中，找出对糖果大小需求最小的，然后发给他剩下的糖果中能满足他的最小的糖果，这样得到的分配方案，也就是满足孩子个数最多的方案。

4.4 区间覆盖

 有 n 个区间，区间的起始端点和结束端点分别是 [l₁, r₁]，[l₂, r₂]，[l₃, r₃]，……，[l_n, r_n]。我们从这 n 个区间中选出一部分区间，这部分区间满足两两不相交（端点相交的情况不算相交），最多能选出多少个区间呢？

假设这 n 个区间中最左端点是 l_min，最右端点是 r_max。这个问题就相当于，选择几个不相交的区间，从左到右将 [l_min, r_max] 覆盖上。按照起始端点从小到大的顺序对这 n 个区间排序。

每次选择的时候，左端点跟前面的已经覆盖的区间不重合的，右端点又尽量小的，这样可以让剩下的未覆盖区间尽可能的大，就可以放置更多的区间。这实际上就是一种贪心的选择方法。

 

 

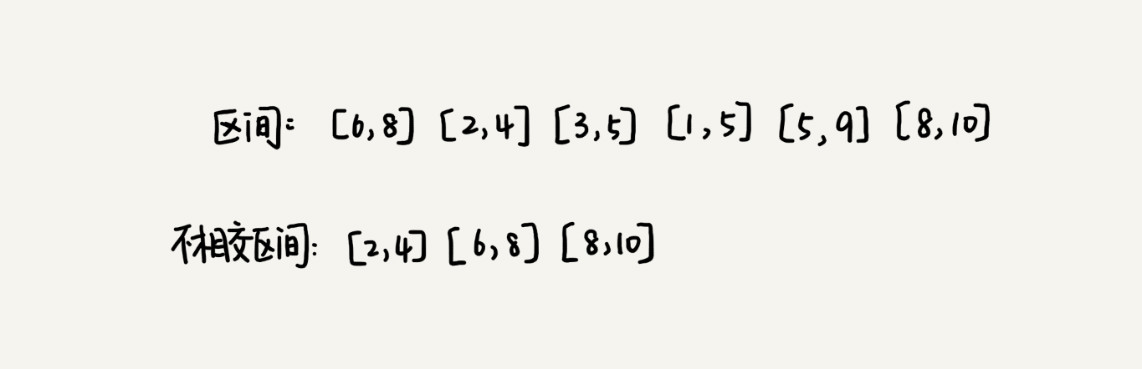
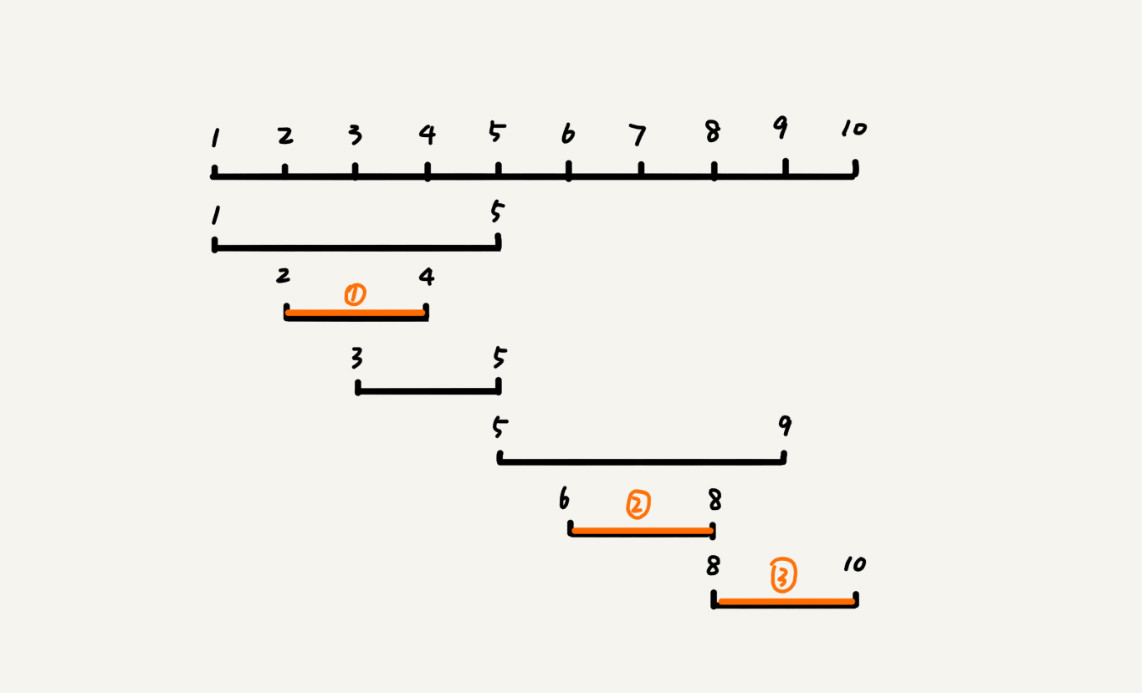
4.5 霍夫曼编码

wiki哈夫曼树链接：https://zh.wikipedia.org/wiki/%E9%9C%8D%E5%A4%AB%E6%9B%BC%E7%BC%96%E7%A0%81 

有一个包含 1000 个字符的文件，每个字符占 1 个 byte（1byte=8bits），存储这 1000 个字符就一共需要 8000bits，那有没有更加节省空间的存储方式呢？

通过统计分析发现，这 1000 个字符中只包含 6 种不同字符，假设它们分别是 a、b、c、d、e、f。而 3 个二进制位（bit）就可以表示 8 个不同的字符，所以，为了尽量减少存储空间，每个字符我们用 3 个二进制位来表示。那存储这 1000 个字符只需要 3000bits 就可以了，比原来的存储方式节省了很多空间。不过，还有没有更加节省空间的存储方式呢？

　　a(000)、b(001)、c(010)、d(011)、e(100)、f(101)

霍夫曼编码不仅会考察文本中有多少个不同字符，还会考察每个字符出现的频率，根据频率的不同，选择不同长度的编码。霍夫曼编码试图用这种不等长的编码方法，来进一步增加压缩的效率。如何给不同频率的字符选择不同长度的编码呢？根据贪心的思想，我们可以把出现频率比较多的字符，用稍微短一些的编码；出现频率比较少的字符，用稍微长一些的编码。
霍夫曼编码就要登场了。霍夫曼编码是一种十分有效的编码方法，广泛用于数据压缩中，其压缩率通常在 20%～90% 之间。

对于等长的编码来说，我们解压缩起来很简单。比如刚才那个例子中，我们用 3 个 bit 表示一个字符。在解压缩的时候，我们每次从文本中读取 3 位二进制码，然后翻译成对应的字符。但是，霍夫曼编码是不等长的，每次应该读取 1 位还是 2 位、3 位等等来解压缩呢？这个问题就导致霍夫曼编码解压缩起来比较复杂。为了避免解压缩过程中的歧义，霍夫曼编码要求各个字符的编码之间，不会出现某个编码是另一个编码前缀的情况。

 

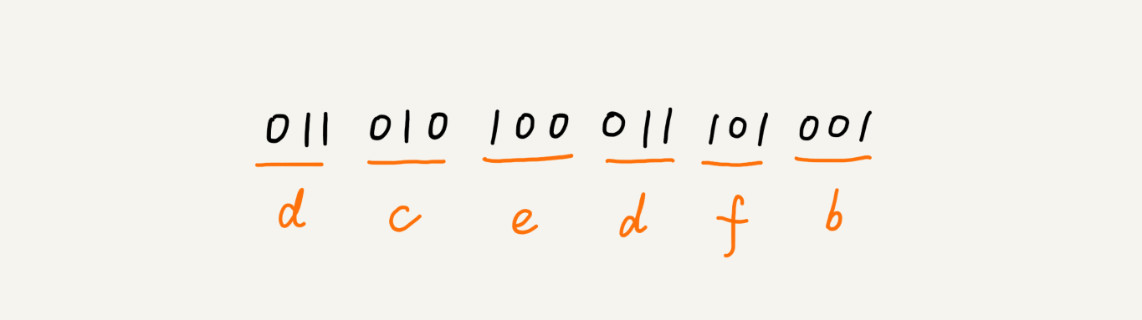
 假设这 6 个字符出现的频率从高到低依次是 a、b、c、d、e、f。我们把它们编码下面这个样子，任何一个字符的编码都不是另一个的前缀，在解压缩的时候，我们每次会读取尽可能长的可解压的二进制串，所以在解压缩的时候也不会歧义。经过这种编码压缩之后，这 1000 个字符只需要 2100bits 就可以了。

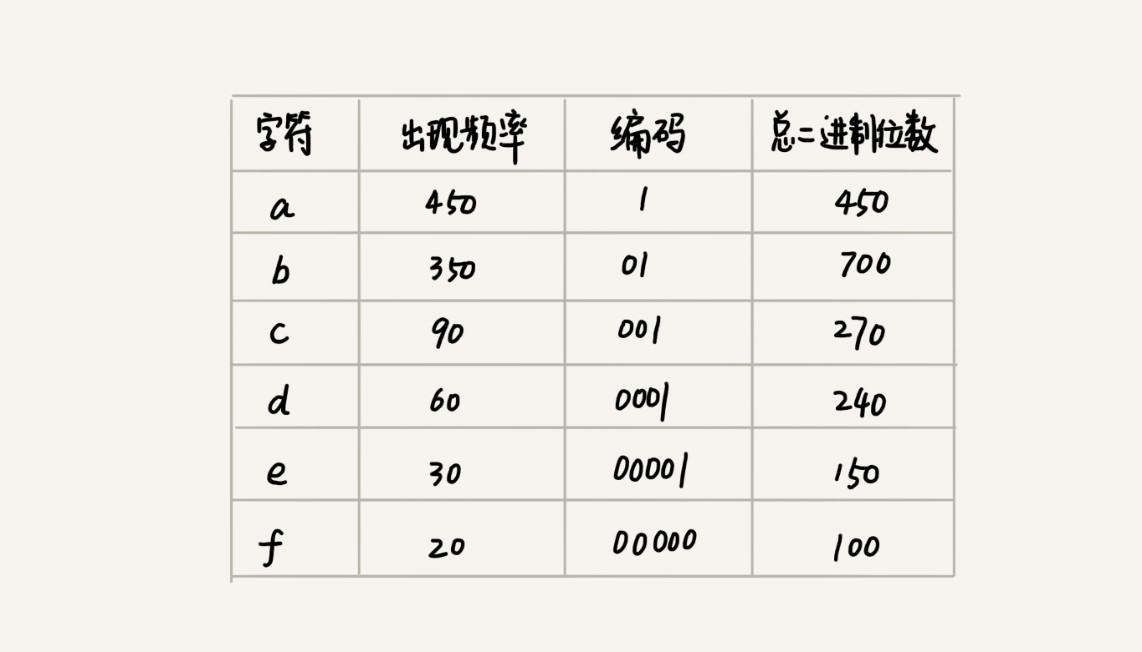
霍夫曼编码的思想并不难理解，但是如何根据字符出现频率的不同，给不同的字符进行不同长度的编码呢？这里的处理稍微有些技巧。

我们把每个字符看作一个节点，并且辅带着把频率放到优先级队列中。我们从队列中取出频率最小的两个节点 A、B，然后新建一个节点 C，把频率设置为两个节点的频率之和，并把这个新节点 C 作为节点 A、B 的父节点。最后再把 C 节点放入到优先级队列中。重复这个过程，直到队列中没有数据。

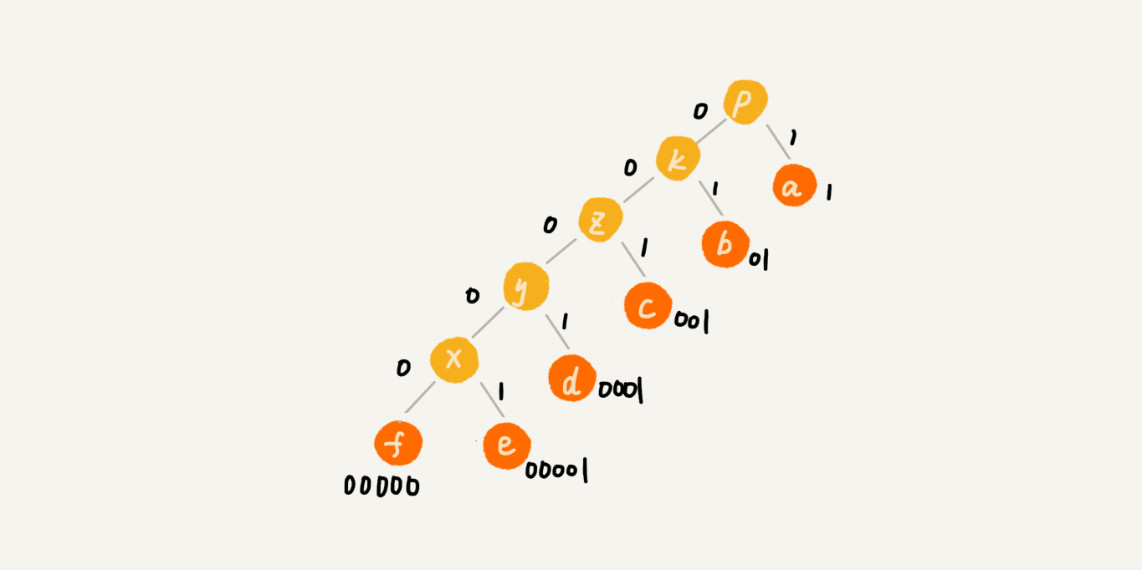
 给每一条边加上画一个权值，指向左子节点的边我们统统标记为 0，指向右子节点的边，我们统统标记为 1，那从根节点到叶节点的路径就是叶节点对应字符的霍夫曼编码。

 

 贪心算法适用的场景比较有限。这种算法思想更多的是指导设计基础算法。比如最小生成树算法、单源最短路径算法。

    如何将要解决的问题抽象成贪心算法模型，贪心算法解决问题的正确性虽然很多时候都看起来是显而易见的，但是要严谨地证明算法能够得到最优解，并不是件容易的事。所以，很多时候，只需要多举几个例子，看一下贪心算法的解决方案是否真的能得到最优解就可以了。

 

1. 在一个非负整数 a 中，我们希望从中移除 k 个数字，让剩下的数字值最小，如何选择移除哪 k 个数字呢？

 　　      由最高位开始，比较低一位数字，如高位大，移除，若高位小，则向右移一位继续比较两个数字，直到高位大于低位则移除，循环k次，如：
　　　　　　4556847594546移除5位-》455647594546-》45547594546-》4547594546-》4447594546-》444594546

　　2. 假设有 n 个人等待被服务，但是服务窗口只有一个，每个人需要被服务的时间长度是不同的，如何安排被服务的先后顺序，才能让这 n 个人总的等待时间最短？

　　　　由等待时间最短的开始服务