数据结构-08 | 图
1. 图的概念
树是非线性表数据结构，图（Graph）也是另一种非线性表数据结构。
树中的元素称为节点，图中的元素叫作顶点（vertex）。图中的一个顶点可以与任意其他顶点建立连接关系。这种建立的关系叫作边（edge）。比如社交网络就是一种典型的图结构。
跟顶点相连接的边的条数叫作顶点的度（degree）。（如微信中 把每个用户看作一个顶点。如果两个用户之间互加好友，那就在两者之间建立一条边；其中，每个用户有多少个好友，对应到图中，就叫作顶点的度。 ）
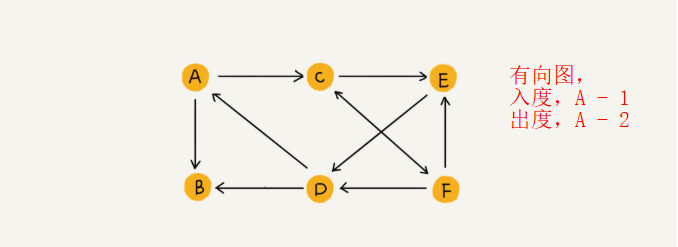
有方向的图叫作“有向图”。 （微博中可以单向关注，如果用户 A 关注了用户 B，我们就在图中画一条从 A 到 B 的带箭头的边，来表示边的方向。如果用户 A 和用户 B 互相关注了，那我们就画一条从 A 指向 B 的边，再画一条从 B 指向 A 的边）
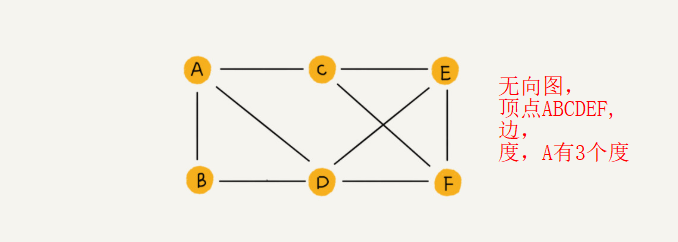
以此类推，我们把边没有方向的图就叫作“无向图”。
无向图中有“度”这个概念，表示一个顶点有多少条边。在有向图中，把度分为入度（In-degree）和出度（Out-degree）。
顶点的入度，表示有多少条边指向这个顶点；顶点的出度，表示有多少条边是以这个顶点为起点指向其他顶点。 （微博的例子，入度就表示有多少粉丝，出度就表示关注了多少人。）
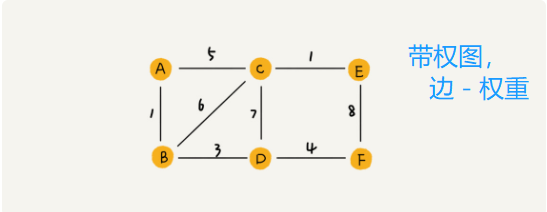
带权图（weighted graph）。在带权图中，每条边都有一个权重（weight），我们可以通过这个权重来表示 QQ 好友间的亲密度。 （QQ 不仅记录了用户之间的好友关系，还记录了两个用户之间的亲密度）
微信无向图、微博有向图、QQ带权图；
2. 图的存储
2.1 邻接矩阵（Adjacency Matrix）
图最直观的一种存储方法就是，邻接矩阵（Adjacency Matrix）， 邻接矩阵的底层依赖一个二维数组。
- 对于无向图来说，如果顶点 i 与顶点 j 之间有边，我们就将 A[i][j] 和 A[j][i] 标记为 1；
- 对于有向图来说，如果顶点 i 到顶点 j 之间，有一条箭头从顶点 i 指向顶点 j 的边，那我们就将 A[i][j] 标记为 1。同理，如果有一条箭头从顶点 j 指向顶点 i 的边，我们就将 A[j][i] 标记为 1。
- 对于带权图，数组中就存储相应的权重。
邻接矩阵来表示一个图，虽然简单、直观，但是比较浪费存储空间。
对于无向图来说，如果 A[i][j] 等于 1，那 A[j][i] 也肯定等于 1。实际上，我们只需要存储一个就可以了。也就是说，无向图的二维数组中，如果我们将其用对角线划分为上下两部分，那我们只需要利用上面或者下面这样一半的空间就足够了，另外一半白白浪费掉了。
还有，如果我们存储的是稀疏图（Sparse Matrix），也就是说，顶点很多，但每个顶点的边并不多，那邻接矩阵的存储方法就更加浪费空间了。
优点：
首先，邻接矩阵的存储方式简单、直接，因为基于数组，所以在获取两个顶点的关系时，就非常高效。
其次，用邻接矩阵存储图的另外一个好处是方便计算。这是因为，用邻接矩阵的方式存储图，可以将很多图的运算转换成矩阵之间的运算。比如求解最短路径问题时会提到一个Floyd-Warshall 算法，就是利用矩阵循环相乘若干次得到结果。
/** * 有向无权图: 邻接矩阵 */ public class GraphArray { private int v; //顶点个数 private boolean matrix[][]; public GraphArray(int v) { this.v = v; matrix = new boolean[v][v]; //默认都是false } public void addEdge(int s, int t) { //添加s到t的边 matrix[s][t] = true; //无向无权图 matrix[s][t] = true; matrix[t][s] = true; } }
2.2 邻接表（Adjacency List）
在图中，如果两个点相互连通，即通过其中一个顶点，可直接找到另一个顶点，则称它们互为邻接点。（邻接指的是图中顶点之间有边或者弧的存在。）
邻接表存储图的实现方式是，给图中的各个顶点独自建立一个链表，用节点存储该顶点，用链表中其他节点存储各自的临界点。
每个顶点对应一条链表，链表中存储的是与这个顶点相连接的其他顶点。
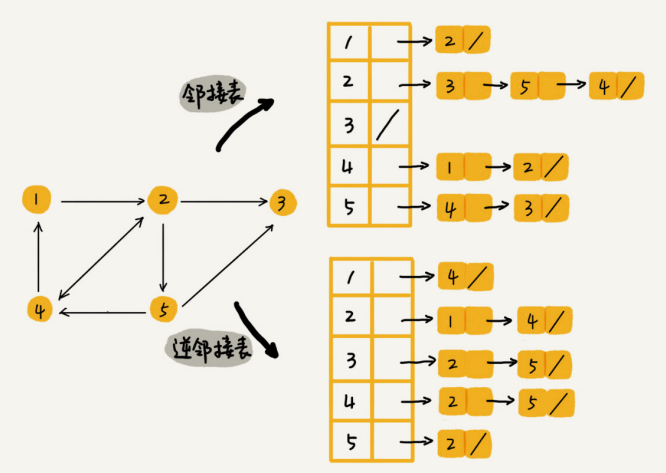
下图是一个有向图的邻接表存储方式，每个顶点对应的链表里面，存储的是指向的顶点。
对于无向图来说，也是类似的，不过，每个顶点的链表中存储的，是跟这个顶点有边相连的顶点
/** * 有向无权图: 邻接表 */ public class GraphLinkedList { private int v; //顶点的个数 private LinkedList<Integer> adj[];//邻接表, 链表数组,每一维对应一个顶点 public GraphLinkedList(int v) { this.v = v; adj = new LinkedList[v];//v个顶点, 每个顶点对应一个 链表 for (int i = 0; i < v; i++) { adj[i] = new LinkedList<>(); } } public void addEdge(int s, int t) { adj[s].add(t);//添加 到链表尾部 有向无权图 } }
邻接矩阵 VS 邻接表
邻接矩阵存储起来比较浪费空间，但是使用起来比较节省时间。
相反，邻接表存储起来比较节省空间，但是使用起来就比较耗时间。（时间、空间复杂度互换的设计思想）
就像图中的例子，如果我们要确定，是否存在一条从顶点 2 到顶点 4 的边 ？
那我们就要遍历顶点 2 对应的那条链表，看链表中是否存在顶点 4。而且，我们前面也讲过，链表的存储方式对缓存不友好。所以，比起邻接矩阵的存储方式，在邻接表中查询两个顶点之间的关系就没那么高效了。
在基于链表法解决冲突的散列表中，如果链过长，为了提高查找效率，可以将链表换成其他更加高效的数据结构，比如平衡二叉查找树等。邻接表长得很像散列。所以，可以将邻接表同散列表一样进行“改进升级”。
可以将邻接表中的链表改成平衡二叉查找树。实际开发中，我们可以选择用红黑树。这样就可以更加快速地查找两个顶点之间是否存在边了。当然，这里的二叉查找树可以换成其他动态数据结构，比如跳表、散列表等。除此之外，我们还可以将链表改成有序动态数组，可
以通过二分查找的方法来快速定位两个顶点之间否是存在边。
3. 应用
在微博中，两个人可以互相关注；在微信中，两个人可以互加好友。 微博、微信是两种“图”，前者是有向图（入度和出度概念），后者是无向图（度的概念）。
微博，微博允许单向关注，微博的入度就表示有多少粉丝，出度就表示关注了多少人。
QQ 不仅记录了用户之间的好友关系，还记录了两个用户之间的亲密度 --- 带权图（weighted graph）。在带权图中，每条边都有一个权重（weight），我们可以通过这个权重来表示 QQ 好友间的亲密度。
如何存储微博、微信等社交网络中的 好友关系？
针对微博用户关系，假设我们需要支持下面这样几个操作：
- 判断用户 A 是否关注了用户 B；
- 判断用户 A 是否是用户 B 的粉丝；
- 用户 A 关注用户 B；
- 用户 A 取消关注用户 B；
- 根据用户名称的首字母排序，分页获取用户的粉丝列表；
- 根据用户名称的首字母排序，分页获取用户的关注列表。
因为社交网络是 一张稀疏图，使用邻接矩阵存储比较浪费存储空间。所以，这里我们采用邻接表来存储。
不过，用一个邻接表来存储这种有向图是不够的。我们去查找某个用户关注了哪些用户非常容 易，但是如果要想知道某个用户都被哪些用户关注了，也就是用户的粉丝列表，是非常困难的。
基于此，我们需要一个逆邻接表。邻接表中存储了用户的关注关系，逆邻接表中存储的是用户的 被关注关系。对应到图上，邻接表中，每个顶点的链表中，存储的就是这个顶点指向的顶点，逆 邻接表中，每个顶点的链表中，存储的是指向这个顶点的顶点。如果要查找某个
用户关注了哪些 用户，我们可以在邻接表中查找；如果要查找某个用户被哪些用户关注了，我们从逆邻接表中查找。
基础的邻接表不适合快速判断两个用户之间是否是关注与被关注的关系，所以我们选择改进版 本，将邻接表中的链表改为支持快速查找的动态数据结构。选择哪种动态数据结构呢？红黑树、 跳表、有序动态数组还是散列表呢？
因为我们需要按照用户名称的首字母排序，分页来获取用户的粉丝列表或者关注列表，用跳表这 种结构再合适不过了。这是因为，跳表插入、删除、查找都非常高效，时间复杂度是 O(logn)， 空间复杂度上稍高，是 O(n)。最重要的一点，跳表中存储的数据本来就是有序的
了，分页获取 粉丝列表或关注列表，就非常高效。
如果对于小规模的数据，比如社交网络中只有几万、几十万个用户，我们可以将整个社交关系存 储在内存中，上面的解决思路是没有问题的。但是如果像微博那样有上亿的用户，数据规模太 大，我们就无法全部存储在内存中了。这个时候该怎么办呢？ 我们可以通过哈希算
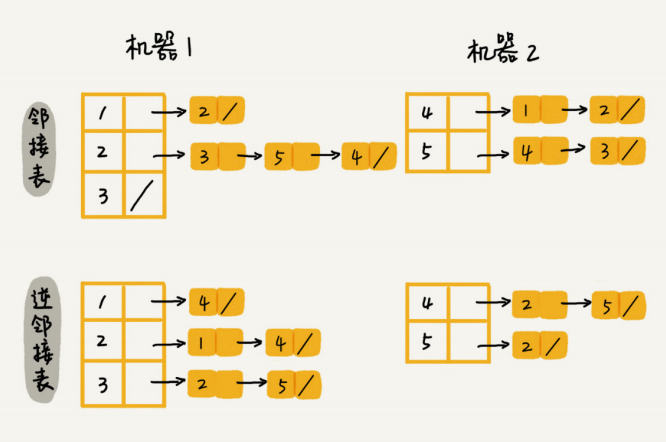
法等数据分片方式，将邻接表存储在不同的机器上。你可以看下面这幅图， 我们在机器 1 上存储顶点 1，2，3 的邻接表，在机器 2 上，存储顶点 4，5 的邻接表。逆邻接 表的处理方式也一样。当要查询顶点与顶点关系的时候，我们就利用同样的哈希算法，先定位顶 点所在
的机器，然后再在相应的机器上查找。
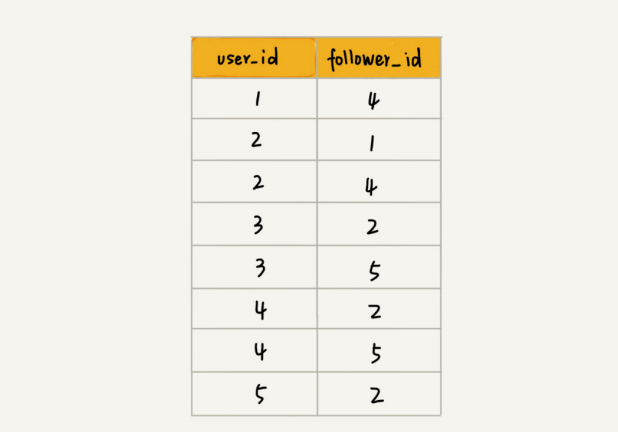
除此之外，我们还有另外一种解决思路，就是利用外部存储（比如硬盘），因为外部存储的存储 空间要比内存会宽裕很多。数据库是我们经常用来持久化存储关系数据的，所以我这里介绍一种 数据库的存储方式。 我用下面这张表来存储这样一个图。为了高效地支持前面定
义的操作，我们可以在表上建立多个 索引，比如第一列、第二列，给这两列都建立索引。
1. 微信好友关系存储方式。无向图，也可以使用邻接表的方式存储每个人所对应的好友列 表。为了支持快速查找，好友列表可以使用红黑树存储。
2. 生活工作中应用图的例子。很多，互联网上网页之间通过超链接连接成一张有向图；城市 乃至全国交通网络是一张加权图；人与人之间的人际关系够成一张图，著名的六度分割理论 据说就是基于这个得到的。
