算法-02 | 分治| 回溯
算法的开章，递归是实现其他高级算法如深度优先、分治等的基础；
碰到一个题目就找它的重复性，重复性有最近的重复性（根据重复性怎么构造怎么分解-->分治、回溯等办法，本质就是递归），或者最优重复性（即动态规划）。
本质上就是找它的重复性。
找重复性以及分解问题，最后组合每个子问题的结果。
1. 分治 Divide & Conquer
分治算法（divide and conquer）的核心思想，分而治之 ，即将原问题划 分成 n 个规模较小，并且结构与原问题相似的子问题，递归地解决这些子问题（庖丁解牛，依次对子问题进行分析），然后再合并其 结果，就得到原问题的解。
分治算法是一种处理问题的思想，递归是一种编程技巧。
分治算法的递归实现中，每一层递归都会涉及这样三个操作：
- 分解：将原问题分解成一系列子问题；
- 解决：递归地求解各个子问题，若子问题足够小，则直接求解；
- 合并：将子问题的结果合并成原问题。
分治算法能解决的问题，一般需要满足下面这几个条件：
- 原问题与分解成的小问题具有相同的模式；
- 原问题分解成的子问题可以独立求解，子问题之间没有相关性，这一点是分治算法跟动态规 划的明显区别，等我们讲到动态规划的时候，会详细对比这两种算法；
- 具有分解终止条件，也就是说，当问题足够小时，可以直接求解；
- 可以将子问题合并成原问题，而这个合并操作的复杂度不能太高，否则就起不到减小算法总 体复杂度的效果了。
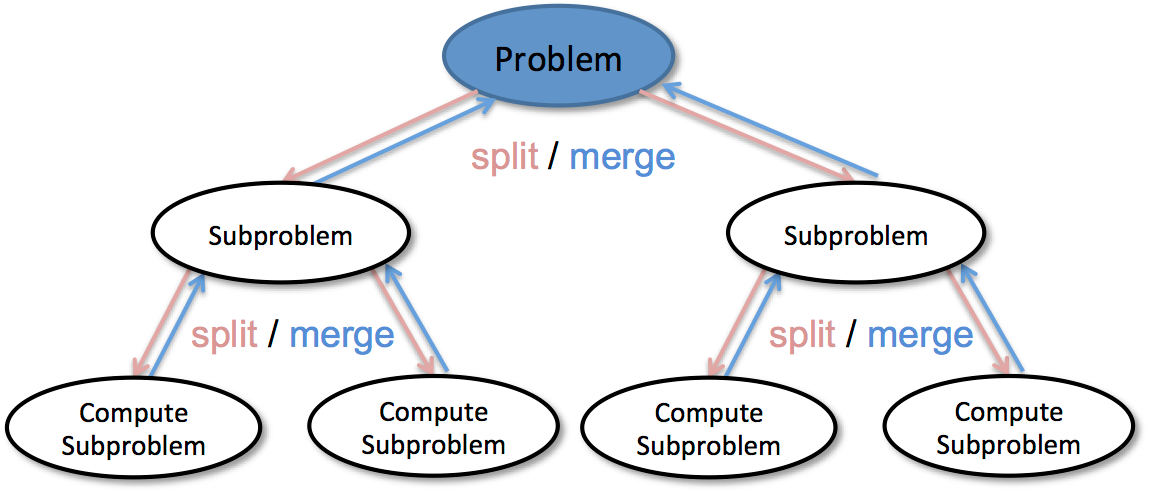
例子：给定一个字符串，把它的每个字符都变成大写；
可以写循环，或者递归
如上图做法的好处是可以并行计算，每个子问题是互不相关的，可以在多核CPU中跑。
分治可以解决的问题，它没有所谓的中间结果（重复计算），如果有大量重复计算如递归分治的效率并不高，这时可以有更适合的算法，比如动态规划、 把中间结果先保存下来下次直接使用。
分治的代码模板：分治一般是用递归来处理的
怎么拆分为子问题，怎么merge这些subresult，得到这些子结果怎么合并起来； 中间的这些子结果如何做质量控制和质量保证，下面的人给你个返回结果你咋知道他做的好还是坏。
专注本层，不要下探。
应用：
如何编程求出一组数据的有序对个数或者逆序对个数呢？
最笨的方法是，拿每个数字跟它后面的数字比较，看有几个比它小的。我们把比它小的数字个数 记作 k，通过这样的方式，把每个数字都考察一遍之后，然后对每个数字对应的 k 值求和，最后 得到的总和就是逆序对个数。不过，这样操作的时间复杂度是 O(n^2)。那有没有更加高效的处 理方法呢？ 我们用分治算法来试试。我们套用分治的思想来求数组 A 的逆序对个数。我们可以将数组分成 前后两半 A1 和 A2，分别计算 A1 和 A2 的逆序对个数 K1 和 K2，然后再计算 A1 与 A2 之间 的逆序对个数 K3。那数组 A 的逆序对个数就等于 K1+K2+K3。
代码：
private int num = 0; public int count(int[] array, int n) { num = 0; mergeSort(array, 0, n - 1); return num; } private void mergeSort(int[] array, int left, int right) { if (left >= right) return; int mid = (left + right) / 2; mergeSort(array, left, mid); mergeSort(array, mid+1, right); merge(array, left, mid, right); } private void merge(int[] array, int left, int mid, int right) { int i = left, j = mid + 1, k = 0; int[] temp = new int[right - left + 1]; while (i <= mid && j <= right) { if (array[i] <= array[j]) { temp[k++] = array[i++]; } else { num += (mid - i + 1); //计数逆序对的个数 temp[k++] = array[j++]; } } while (i <= mid) { temp[k++] = array[i++]; } while (j <= right) { temp[k++] = array[j++]; } for (int p = 0; p < temp.length; p++) { array[left + p] = temp[p]; } }
MapReduce 是 Google 大数据处理的三驾马车之一，MapReduce的本质就是分治算法，另外两个是 GFS 和 Bigtable。另外分治在倒排 索引、PageRank 计算、网页分析等搜索引擎相关的技术中都有大量的应用。
分布式系统中的mapReduce 将一个大问题分成小问题，小问题依次解决后再合并结果返回数据，
如何将10GB 的订单文件按照金额排序 ？
看似一个简单的排序问题，但是因为数据量大有 10GB，而机器的内存可能只有 2、3GB 这样子，无法一次性加载到内存，也就无法通过单纯地使用快排、归并等基础算法来解决了。
要解决这种数据量大到内存装不下的问题，可以利用分治的思想。将海量的数据集合根据某种方法，划分为几个小的数据集合，每个小的数据集合单独加载到内存来解决，然后再将小数据集合合并成大数据集合。
利用这种分治的处理思路，不仅仅能克服内存的限制，还能利用多线程或者多机处理，加快处理的速度。
10GB 的订单排序，先扫描一遍订单，根据订单的金额，将10GB的文件划分为几个金额区间。比如订单金额为1到100 元的放到一个小文件，101到200之间的放到另一个文件，以此类推。
这样每个小文件都可以单独加载到内存排序， 最后将这些有序的小文件合并，就是最终有序的 10GB 订单数据了。
如果订单数据存储在类似 GFS 这样的分布式系统上，当10GB 的订单被划分成多个小文件的时候，每个文件可以并行加载到多台机器上处理，最后再将结果合并在一起，这样并行处理的速度 也加快了很多。
这里需要注意的就是数据的存储与计算所在的机器是同一个或者在网络中靠的很近（比如一个局域网内，数据存取速度很快），否则就会因为数据访问的速度，导致整个处理过程不但不会变快，反而有可能变慢。
10GB 大小，可能还不大。如果处理的数据是 1T、10T、100T，那一台机器处理的效率肯定是非常低的。而对于谷歌搜索 引擎来说，网页爬取、清洗、分析、分词、计算权重、倒排索引等等各个环节中，都会面对如此 海量的数据（比如网页）。所以，利用集群并行处理显然是大势所趋。
一台机器过于低效，就把任务拆分到多台机器上来处理。如果拆分之后的小任务之间互不干扰，独立计算，最后再将结果合并。这就是分治思想。
实际上，MapReduce 框架只是一个任务调度器，底层依赖 GFS 来存储数据，依赖 Borg 管理机器。它从 GFS 中拿数据，交给 Borg 中的机器执行，并且时刻监控机器执行的进度，一旦出现机器宕机、进度卡壳等，就重新从 Borg 中调度一台机器执行。
尽管 MapReduce 的模型非常简单，但是在 Google 内部应用非常广泛。它除了可以用来处理 这种数据与数据之间存在关系的任务，比如 MapReduce 的经典例子，统计文件中单词出现的 频率。除此之外，它还可以用来处理数据与数据之间没有关系的任务，比如对网页分
析、分词 等，每个网页可以独立的分析、分词，
而这两个网页之间并没有关系。网页几十亿、上百亿，如 果单机处理，效率低下，我们就可以利用 MapReduce 提供的高可靠、高性能、高容错的并行 计算框架，并行地处理这几十亿、上百亿的网页。
2. 回溯 Backtrackin
回溯法采用试错的思想，它尝试分步的去解决一个问题。在分步解决问题的过程 中，当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将 取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问 题的答案。
回溯法通常用最简单的递归方法来实现，在反复重复上述的步骤后可能出现两种情况：
- 找到一个可能存在的正确的答案；
- 在尝试了所有可能的分步方法后宣告该问题没有答案。
在最坏的情况下，回溯法会导致一次复杂度为指数时间的计算。
就是不断的在每一层进行试，经典应用是八皇后问题以及数独问题上，简单的比如括号的生成。归去来兮的感觉。
回溯法:
回溯法采用试错的思想，它尝试分步的去解决一个问题。在分步解决问题的过程中，当
它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚
至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案。
回溯法通常用最简单的递归方法来实现，在反复重复上述的步骤后可能出现两种情况：
• 找到一个可能存在的正确的答案
• 在尝试了所有可能的分步方法后宣告该问题没有答案
在最坏的情况下，回溯法会导致一次复杂度为指数时间的计算。
回溯和递归没有太多本质上的区别，只不过它采用一种试错的思想，尝试分布去解决一个问题。就是所谓的分治 + 试错 == 回溯
人脑的第一个问题它回溯的深度不够，因为它的短期记忆比较模糊或者短期记忆记不准，经常回溯了一两层之后就不记得是不是刚刚走的位置了。
第二人比较懒，当你多回溯的几步之后特别累就不再想直接走了。
而机器就擅长做重复的运算，第二它的记忆也是无敌的，机器做这种有重复性的回溯是很牛逼的。
*回溯算法框架。解决一个回溯问题，实际上就是一个决策树的遍历过程。你只需要思考 3 个问题：
* 1、路径：也就是已经做出的选择。
* 2、选择列表：也就是你当前可以做的选择。
* 3、结束条件：也就是到达决策树底层，无法再做选择的条件。
* 回溯算法框架代码:
*
* result = []
* def backtrack(路径, 选择列表):
* if 满足结束条件:
* result.add(路径)
* return
*
* for 选择 in 选择列表:
* 做选择
* backtrack(路径, 选择列表) -- 递归
* 撤销选择
* 链接：https://leetcode-cn.com/problems/permutations/solution/hui-su-suan-fa-xiang-jie-by-labuladong-2/
* 来源：力扣（LeetCode）
深度优先搜索算法利用的是回溯算法思想。它除了用来指导像深度优先搜索这种经典的算法设计之外，还可以用在很多实际的软件开发场景中，比如正则表达式匹配、编译原理中的语法分析等，除此之外，很多经典的数学问题都可以用回溯算法解决，比如数独、八皇后、0-1 背包、图的着色、旅行商问题、全排列等等。
贪心算法，在每次面对岔路口的时候，都做出看起来优的选择，期望这一组选择可以使得我们的人生达到“优”。但是，贪心算法并不一定能得到全局优解。
电影《蝴蝶效应》，讲的就是主人公为了达到自己的目标，一直通过回溯的方法，回到童年，在关键的岔路口，重新做选择。当然我们的人生是无法倒退的，但是这其中蕴含的思想就是回溯算法。
回溯算法很多时候都应用在“搜索”这类问题上。这里搜索，并不是狭义的指图的搜索算法，而是在一组可能的解中，搜索满足期望的解。
回溯的处理思想，有点类似枚举搜索。枚举所有的解，找到满足期望的解。为了有规律地枚举所有可能的解，避免遗漏和重复，把问题求解的过程分为多个阶段。每个阶段，我们都会面对一个岔路口，我们先随意选一条路走，当发现这条路走不通的时候（不符合期望的
解），就 回退到上一个岔路口，另选一种走法继续走。
8皇后问题
8x8 的棋盘，希望往里放 8 个棋子（皇后），每个棋子所在的行、列、对角线都不 能有另一个棋子。
把这个问题划分成 8 个阶段，依次将 8 个棋子放到第一行、第二行、第三行……第八行。在 放置的过程中，我们不停地检查当前的方法，是否满足要求。如果满足，则跳到下一行继续放置 棋子；如果不满足，那就再换一种方法，继续尝试。
92种排列方式如下：
Q * * * * * * * * * * * Q * * * * * * * * * * Q * * * * * Q * * * * Q * * * * * * * * * * * Q * * Q * * * * * * * * * Q * * * * Q * * * * * * * * * * * * Q * * * * * * * * * Q * * Q * * * * * * * * * * * Q * * * * Q * * * * * Q * * * * * * * * * * Q * * * Q * * * * * * * * * * * * * Q * * * * Q * * * * * * * * * Q * * * * * * * * * Q * Q * * * * * * * * * * Q * * * * * Q * * * * * Q * * * * * * * * * * * * * Q * * * * * Q * * * * * * * * * * Q * Q * * * * * * * * * Q * * * * * * * * * Q * * * * Q * * * * * * Q * * * * * * * * * Q * * * * * * * * * Q * * * * * * * * * Q * * Q * * * * * Q * * * * * * * * * * * * * Q * * * * * Q * * * * Q * * * * * * * * * * Q * * * * * * * * * Q * Q * * * * * * * * * Q * * * * * * * * * * * * Q * * * * * Q * * * * * Q * * * * * Q * * * * * * * * * * Q * * * * * * * * * Q * * * * Q * * * * Q * * * * * * * * * * * * * * Q * * * * * Q * * * * Q * * * * * * Q * * * * * * * * * * * Q * * Q * * * * * * * * * * * * * Q * * * * Q * * * * * * * * * * * Q * * Q * * * * * * * * * Q * * * * Q * * * * * * * * * * * Q * * * * * * * * * Q * * Q * * * * * Q * * * * * * * * * * Q * * * * * * * * * * Q * * * * * Q * * * * Q * * * * * * * * * * * * Q * * * Q * * * * * * * * * * Q * * * * * * * * * Q * * * * Q * * * Q * * * * * * * * * * Q * * * * * Q * * * * * * * * * * * * Q * * * * * Q * * * * * * * * * * Q Q * * * * * * * * * * Q * * * * * * * * * Q * * * * Q * * * * * * Q * * * * * * * * * * * * * Q * * * * * Q * * Q * * * * * * * * * Q * * * * * * * * * Q * * * * * * * * * Q * * * * Q * * * * * * Q * * * * * Q * * * * * * * * * * * * * Q * * * * * Q * * * * * * * * * * Q * Q * * * * * * * * * Q * * * * * * * * * Q * * * * Q * * * * * * * * * Q * * * * Q * * * * * * * * * * * * * Q Q * * * * * * * * * * * * * Q * * * * Q * * * * * * * * * Q * * * * Q * * * * * * * * * Q * * * * Q * * * * * * * * * * * * * Q * * * * * Q * * * * * Q * * * * * * * * * * Q * Q * * * * * * * * * Q * * * * * * * * * Q * * * * * * * * * Q * Q * * * * * * * * * * Q * * * * * Q * * * * * * * * * * * * * Q * * * * * Q * * * * Q * * * * * * * * * Q * * * * * * * * * * Q * * * Q * * * * Q * * * * * * * * * * * * * Q * * Q * * * * * * * * * * * Q * * * * Q * * * * * * * * * * Q * * * Q * * * * * * * * * * Q * * * * * * * * * * Q Q * * * * * * * * * * * * * Q * * * * Q * * * * * * Q * * * * * * * * * * Q * * * Q * * * * * * * * * * * * Q * Q * * * * * * * * * * Q * * * * * * * * * * * Q * * * * Q * * * * * Q * * * * * * * * * * Q * * * Q * * * * * * * * * * * * Q * * * * * Q * * * Q * * * * * * * * * * * * * * Q * * * Q * * * * * * Q * * * * * * * * * * Q * * * * * Q * * * * Q * * * * * * * * * * * * * * Q * * * * Q * * * * * * * * * Q * * Q * * * * * * * * Q * * * * * * * * * * Q * * * * * Q * * * * * Q * * * * * * * * * * * * * Q * * * * Q * * * * * * * * * Q * Q * * * * * * * * * Q * * * * * * * * * * Q * * * * * * * * * Q Q * * * * * * * * * * Q * * * * * * * * * * Q * * * * * Q * * * * Q * * * * * * * * Q * * * * * * * * * * Q * * * * * * * * * Q Q * * * * * * * * * * * Q * * * * * * * * * Q * * Q * * * * * * * * * Q * * * * * * Q * * * * * * * * * * Q * * * * * * * * * Q * Q * * * * * * * * * Q * * * * Q * * * * * * * * * * * * * Q * * * * * Q * * * * * Q * * * * * * * * * * * Q * * Q * * * * * * * * * * * * * Q * * * * Q * * * Q * * * * * * * * * * Q * * * * * * * * * Q * * * * Q * * * * * * * * * * * Q * * Q * * * * * * * * * * * * * Q * * * * * Q * * * * * Q * * * * Q * * * * * * * * * * * Q * * * * * Q * * * * * * * * * * * * Q * * * Q * * * * * * * * * * Q * Q * * * * * * * * * * * * Q * * * Q * * * * * * * * * * Q * * * * * * Q * * * * Q * * * * * * * * * * * Q * * * * * * * * * * Q * Q * * * * * * * * * * * * Q * * * Q * * * * * * * * * * Q * * * * * Q * * * * Q * * * * * * * * * * * Q * * * * * * * * * * Q * * * * * Q * * * * Q * * * * * * * * * * * Q * * Q * * * * * * * * * Q * * * * * Q * * * * * * * * * * Q * * * * * * * * * * Q * * * * * Q * * Q * * * * * * * * * Q * * * * * * * * * * * Q * * * * Q * * * * * Q * * * * * * * * * * * * Q * * * Q * * * * * * * * * * Q * * * * * * * * * Q Q * * * * * * * * * * * Q * * * * * * Q * * * * * Q * * * * * * * * * * * * Q * * * Q * * * * * * * * * * Q * * * * * * * * * Q * * * * Q * * * Q * * * * * * * * * * Q * * * * * Q * * * * * * * * * * * * Q * * * * * Q * * * Q * * * * * * * * * * * * * * Q * * * * * Q * * * * Q * * * * * * * * Q * * * * * Q * * * * * * * * * * * * * Q * * * * Q * * * * * * * * * Q * Q * * * * * * * * * Q * * * * * * * * * * Q * * * * * Q * * * * * Q * * * * * * * * * * * * * Q * * * * * Q * * Q * * * * * * * * * Q * * * * * * * * * Q * * * * * * * * * Q * * * * Q * * * * * * * * * Q * * Q * * * * * * * * * * * Q * * * * Q * * * * * * * * * * * * * Q * * Q * * * * * * * * * * * Q * * * * Q * * * * * * * * * Q * * * * * * * * * Q * Q * * * * * * * * * * * * Q * Q * * * * * * * * * Q * * * * * * * * * Q * * * * * * Q * * * * * * * * * Q * * * * * * * * * Q * * Q * * * * * Q * * * * * * * * * * * * * Q * * * * * Q * * * * Q * * * * * * * * * Q * * * * * * * * * * Q * Q * * * * * * * * * * * * * * Q * * * * Q * * * * Q * * * * * * * * * * * Q * * * * Q * * * * * * * * Q * * * * * * * * * * Q * * * Q * * * * * * * * * * * * Q * Q * * * * * * * * * * Q * * * Q * * * * * * * * * * * * Q * * * * * Q * * * * * * * * * * Q * * * * * Q * * * * Q * * * * * * * * * * * Q * * Q * * * * * * * * * Q * * * * * * * * * * * * Q * * * Q * * * * * * * * * * Q * * * * * Q * * * * * Q * * * * * Q * * * * * * * * * * * * Q * * * * * * * * * Q * Q * * * * * * * * * Q * * * * * * * * * * * Q Q * * * * * * * * * Q * * * * * * * * * * Q * * * Q * * * * * * * * * * * * Q * * * * * Q * * * * * * Q * * * * * * * * * * * Q Q * * * * * * * * * * * Q * * * * * * * * * Q * * Q * * * * * * * * * * * Q * * * * Q * * * * * * * * Q * * * * * * * * * * * Q * * * * Q * * * * * Q * * * * * Q * * * * * * * * * * * * * Q * * Q * * * * * * * * * * * Q * * * * * * Q * * * Q * * * * * * * * * * Q * * * * * * * * * Q * * * * * * * * * Q * Q * * * * * * * * * * * * Q * * * Q * * * * * * * * * Q * * * Q * * * * * * * * * * * * * * Q * * * Q * * * * * Q * * * * * * * * * * * * Q * * * Q * * * * * * * * * * Q * * * * * * Q * * * Q * * * * * * * * * * * * * * Q * * * * * Q * * * * Q * * * * * * * * * * * Q * * Q * * * * * * * * * Q * * * * * * * * Q * * * * Q * * * * * * * * * Q * * * * * * * * * Q * * * * * * * * * Q * * Q * * * * * Q * * * * * * * * * * * * * Q * * * * * Q * * * * Q * * * * * * * * * Q * * * * * * * * * * Q * * * Q * * * * * * * * * * * * Q * * * * * Q * * Q * * * * * * * * * * * Q * * * * Q * * * * * * * * * * * Q * * Q * * * * * * * * * * * * * Q * * * * Q * * * * * * * * * * * Q * * Q * * * * * * * * * Q * * * * Q * * * * * * * * * * * * * Q Q * * * * * * * * * * Q * * * * * * * * * * Q * * * Q * * * * * * * * * * Q * * * * * * Q * * * * * Q * * * * * Q * * * * * * * * * * * * Q * * * * * * * * * Q * Q * * * * * * * * * Q * * * * * * * * * * Q * * * * * Q * * * * * Q * * * * * Q * * * * * * * * * * * * * Q * * Q * * * * * * * * * * * * * Q * * * * * Q * * * * * Q * * * * * * * * Q * * * * * Q * * * * * * * * * * * * Q * * * Q * * * * * * * * * * Q * Q * * * * * * * * * * * * Q * * * Q * * * * * * * * * * Q * * * * * * * * * Q * Q * * * * * * * * * Q * * * * * * * * * * * * Q * * * * * Q * * * * * Q * * * * * Q * * * * * * * * * * Q * * * * * * * * * Q * Q * * * * * * * * * * Q * * * * * Q * * * * * * * * * * * * * Q * * * * * Q * * * * Q * * * * * * * * * Q * * * * * * * * * Q * * Q * * * * * * * * * Q * * * * * * * * * * * Q Q * * * * * * * * * Q * * * * * * * * * * Q * * * * * * Q * * * * * * * * * Q * * Q * * * * * * * * * * * Q * * * * Q * * * * * Q * * * * * * * * * * Q * * * * * * * * * * * Q * * * * Q * * * * * * * * * Q * * Q * * * * * * * * * * * Q * * * * Q * * * * * Q * * * * * * * * * * * * * * Q * * * Q * * * * * * * * Q * * * * * * * * * Q * * * * Q * * * * Q * * * * * * * * * Q * * * * * * * * * * * * Q * * * * * Q * * * Q * * * * * * * * * * Q * * * * * * * * * * Q * * * Q * * * * Q * * * * * * * * * Q * * * * * * * * * * Q * * * Q * * * * * * * * * * * * Q * * * * * Q * * * * * * * * * * Q * * * Q * * * * Q * * * * * * * * * * * * * Q * * Q * * * * * * * * * * * Q * * * * Q * * * * * * * * * * Q * * Q * * * * * * * * * * * Q * * * * Q * * * * * * * * * * * * * Q * * Q * * * * * * * * * * * Q * * * * Q * * * * * * * * * Q * * * Q * * * * * * * * * * * * Q * Q * * * * * * * * * Q * * * * * * * * * Q * * * * * * * * * * Q * * * Q * * * * * * * * * Q * * * Q * * * * * * * * * * * * Q * Q * * * * * * * * * * Q * * * * * * * * * * * Q * * * * Q * * * * * Q * * * * * * * * * * Q * * * * Q * * * * * Q * * * * * * * * * * * * * Q * * * * * Q * * * * * * * * * * Q * Q * * * * * * * * * Q * * * * * * * * * Q * * * * Q * * * * * Q * * * * * * * * * * * * * * Q * * * Q * * * * * Q * * * * * * * * * * * * Q * * * * * Q * * * * * * * * Q * * * * Q * * * * * Q * * * * * * * * * * * * * * Q * * * * Q * * * * Q * * * * * * * * * Q * * * * * * * * * * Q * * * * * * Q * * * * Q * * * * * * * * * Q * * * * * * * * * Q * Q * * * * * * * * * * Q * * * * * Q * * * * * * * * * * * * * Q * * * * * Q * * * * Q * * * * * * * * * Q * * * * * * * * * * Q Q * * * * * * * * * * Q * * * * * Q * * * * * * * * * * * * Q * * * * * * Q * * * * Q * * * * * * * * * * * Q * * Q * * * * * * * * * Q * * * * * * * * * * * Q Q * * * * * * * * * * * Q * * * * * * * * Q * * * * Q * * * * * * * * * * * Q * * Q * * * * * * * * * * * * * Q * * * * Q * * * Q * * * * * * * * * * Q * * * * * * * * * Q * * * * Q * * * * * * * * * * * Q * * * * Q * * * * Q * * * * * * * * * * * * * * Q * Q * * * * * * * * * * Q * * * * * * * * Q * * * * * Q * * * * Q * * * * * * * * * * * Q * * * * * * * * * * Q * Q * * * * * * * * * * * * Q * * * Q * * * * * * * * * * Q * * * * * Q * * * * * Q * * * * * * * * * * * * * Q * * * * Q * * * * * * * * * Q * Q * * * * * * * * * Q * * * * * * * * * * Q * * * * * Q * * * * * * * * * * Q * Q * * * * * * * * * Q * * * * * * * * * Q * * * * Q * * * * * * * * * * * * * Q * * * * * Q * * * * * Q * * * * * * * * * * Q * Q * * * * * * * * * * * * * * Q * Q * * * * * * * * * * Q * * * * * Q * * * * * * * * * * Q * * * * * * * * * Q * Q * * * * * * * * * Q * * * * Q * * * * * * * * * * * * * Q * * * * * Q * * * * * Q * * * * * * * * * * * Q * Q * * * * * * * * * Q * * * * * * * * * * * * Q * * * * * Q * * * * * Q * * * * * Q * * * * * * * * * * Q * * * * * * * * * Q * * Q * * * * * * * * * Q * * * * Q * * * * * * * * * * * * * * Q * * * * Q * * * * * Q * * * * * * * * * * Q * * * * * * * * Q * * Q * * * * * * * * * * * Q * * * * Q * * * * * Q * * * * * * * * * * Q * * * * * * * * * * * Q * * * * Q * * * * * * * * * Q * * * Q * * * * * Q * * * * * * * * * * * * Q * * * * * * * * * Q * * * * Q * * * * Q * * * * * * * * * Q * * * * * * * * * * Q * * * Q * * * * * * * * * * * * Q * Q * * * * * * * * * * Q * * * Q * * * * * * * * * * * * Q * * * * * Q * * * * * * * * * * Q * * * * Q * * * * * Q * * * * * * * * * * Q * * * * * * * * * * Q Q * * * * * * * * * Q * * * * * * * * * * Q * * * * * * * * Q * * * * Q * * * * * Q * * * * * * * * * * * * * Q * * * * * Q * * Q * * * * * * * * * Q * * * * * * * * * Q * * * * * * * * * Q * * * * * Q * * * * * Q * * * * * Q * * * * * * * * * * * * Q * * * * * * * * * Q * Q * * * * * * * * * Q * * * * * * * * * * * Q * Q * * * * * * * * * Q * * * * Q * * * * * * * * * * * * * Q * * * * * Q * * * * * Q * * * * * * * * * * Q * * * * * * * * * Q * Q * * * * * * * * * * Q * * * * * Q * * * * * Q * * * * * * * * * * * * * Q * * * * Q * * * * * * * * * Q * * * * * * * * * Q * * Q * * * * * Q * * * * * * * * * * * * Q * * * Q * * * * * * * * * * Q * * * * * * * * * Q * * * * Q * * * * * * * * * * * Q * * * Q * * * * Q * * * * * * * * * Q * * * * * * * * * * Q * * * Q * * * * * * * * * * * * Q * * * * * Q * * * 一共92种排列方式
0-1 背包问题
0-1 背包是非常经典的算法问题，很多场景都可以抽象成这个问题模型。这个问题的经典解法是动态规划，不过还有一种简单但没有那么高效的解法，那就回溯算法。0-1 背包问题有很多变体，一种比较基础的是：
我们有一个背包，背包总的承载重量是 Wkg。现在我们有 n 个物品，每个物品的重量不等，并且不可分割。期望选择几件物品，装载到背包中。在不超过背包所能装载重量的前提下，如何让背包中物品的总重量大？（如果物品是可以分割的，可以装某个物品的一部分到背包里面可以使用贪心算法。）
这里的背包问题，物品是不可分割的，要么装要么不装，所以叫 0-1 背包问题。显然，这个问题已经无法通过贪心算法来解决了。用回溯算法如何来解决：
对于每个物品来说，都有两种选择，装进背包或者不装进背包。对于 n个物品来说，总的装法就有 2^n 种，去掉总重量超过 Wkg 的，从剩下的装法中选择总重量接近 Wkg 的。不过，如何才能不重复地穷举出这 2^n 种装法呢？
用回溯的方法，可以把物品依次排列，整个问题就分解为了 n 个阶段，每个阶段对应一个物品怎么选择。先对第一个物品进行处理，选择装进去或者不装进去，然后再递归地处理剩下的物品。
这里还稍微用到了一点搜索剪枝的技巧，就是当发现已经选择的物品的重量超过 Wkg 之后，就停止继续探测剩下的物品。
