数据结构-05 |散列表-① | 映射| 集合
哈希表（HashTable ）& 集合（Set）
1. 哈希（散列）表 HashTable
1.1 概念
哈希表（Hash table），也叫散列表，来源于数组，它借助散列函数对数组这种数据结构进行扩展，利用的是数组支持按照下标随机访问元素的特性，所以散列表其实就是数组的一种扩展，由数组演化而来。可以说，如果没有数组，就没有散列表。
它通过把关键码值映射到表中一个位置（即它的下标index）来访问记录，根据关键码值（Key value）直接访问数据加快了查找的速度。
这个映射函数叫作散列函数（Hash Function）或哈希函数，存放记录的数组叫作哈希表（或散列表）。
散列表用的就是数组支持按照下标随机访问的时候，时间复杂度是 O(1) 的特性。我们通过散列函数把元素的键值映射为下标，然后将数据存储在数组中对应下标的位置。当我们按照键值查询元素时，我们用同样的散列函数，将键值转化数组下标，从对应的数组下标的位置取数据。
假如我们有 89 名选手参加学校运动会。为了方便记录成绩，每个选手胸前都会贴上自己的参赛号码。这 89 名选手的编号依次是 1 到 89。我们希望通过编号快速找到对应的选手信息。参赛编号用6 位数字来表示。比如 051167，其中，前两位 05 表示年级，中间两位 11 表示班级，最后两位还是原来的编号 1 到 89。这时我们该如何存储选手信息，才能支持通过编号来快速查找选手信息呢？
尽管我们不能直接把编号作为数组下标，但可以截取参赛编号的后两位作为数组下标，来存取选手信息数据。当通过参赛编号查询选手信息时，取参赛编号后两位，作为数组下标，来读取数组中的数据。这就是典型的散列思想。其中，参赛选手的编号我们叫作键（key）或者关键字。我们用它来标识一个选手。我们把参赛编号转化为数组下标的映射方法就叫作散列函数（或“Hash 函数”“哈希函数”），而散列函数计算得到的值就叫作散列值（或“Hash 值”“哈希值”）。
通过上例，可总结出这样的规律：散列表用的就是数组支持按照下标随机访问的时候，时间复杂度是 O(1) 的特性。我们通过散列函数把元素的键值映射为下标，然后将数据存储在数组中对应下标的位置。当我们按照键值查询元素时，我们用同样的散列函数，将键值转化数组下标，从对应的数组下标的位置取数据。
1.2 散列（哈希）函数 Hash Function
上例中散列函数的伪代码为：
哈希函数--散列函数，它是一个函数。可把它定义成hash(key)，其中 key 表示元素的键值，hash(key) 的值表示经过散列函数计算得到的散列值。
int hash(String key) {
// 获取后两位字符 后两位为运动员的编号，作为数组下标。
string lastTwoChars = key.substr(length-2, length);
// 将后两位字符转换为整数 hash(key)
int hashValue = convert lastTwoChas to int-type;
return hashValue;
}
如果参赛选手的编号是随机生成的 6 位数字，又或者用的是 a 到 z 之间的字符串，该如何构造散列函数呢？散列函数设计的基本要求：
-
散列函数计算得到的散列值是一个非负整数（因为数组下标是从 0 开始的，所以散列函数生成的散列值也要是非负整数）；
-
如果 key1 = key2，那 hash(key1) == hash(key2) （相同的 key，经过散列函数得到的散列值也应该是相同的。）；
-
如果 key1 ≠ key2，那 hash(key1) ≠ hash(key2)。（这个要求看起来合情合理，但是在真实的情况下，要想找到一个不同的 key 对应的散列值都不一样的散列函数，几乎是不可能的。著名的MD5、SHA、CRC等哈希算法，也无法完全避免这种散列冲突。而且，因为数组的存储空间有限，也会加大散列冲突的概率。）
所以我们几乎无法找到一个完美的无冲突的散列函数，即便能找到，付出的时间成本、计算成本也是很大的，所以针对散列冲突问题，我们需要通过其他途径来解决。
哈希函数的输入域可以是非常大的范围，但是输出域是固定范围，假设为S，哈希函数的性质：
- 典型的哈希函数都拥有无限的输入值域；
- 输入值相同时，返回值一样。
- 输入值不同时，返回值可能一样，也可能不一样。
- 不同输入值得到的哈希值，整体均匀的分布在输出域S上。（这点是评价哈希函数优劣的关键。）
比如“aaa1”、 “aaa2”、“aaa3”，虽然相似，但计算出的哈希值差异巨大。
不同输入值得到的哈希值越均匀分布在S上，该哈希函数越优秀。
输入范围（极大）====经过哈希函数计算后====>> S（输出域）===%m===>> 1,2,3,....m-1（会均匀分布在0~ m-1上）
1.3 哈希碰撞 Hash Collisions（散列冲突）
哈希函数选取的好就会让这些数值尽量分散，而不会发生所谓的碰撞
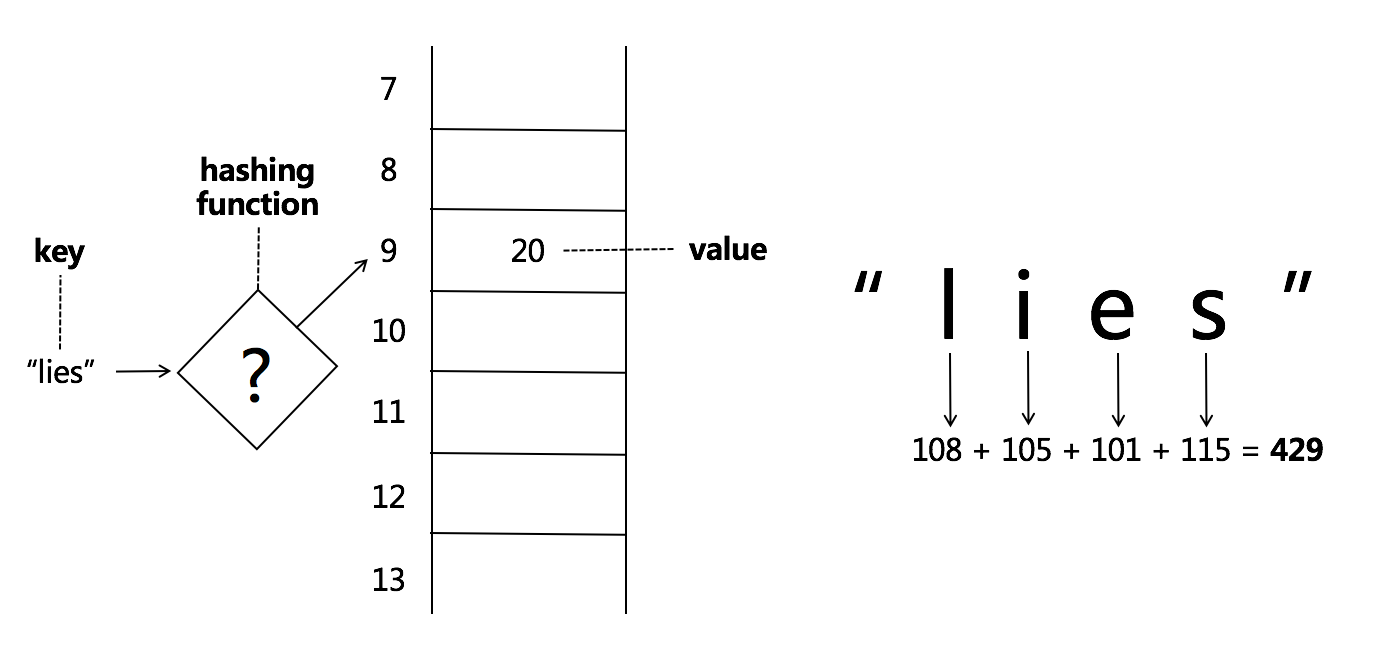
两个key用同样的hash函数最后取模得到的结果下标一样既Hash Collisions（即两个字符串key哈希后得到相同的下标。）
只要有hash函数,99%都会有重复的值既碰撞, 而且把大于30的放在30之内的范围内肯定会有碰撞;
lines和foes 最后得到的下标都是9, 在9的位置上建立一个链表, 所有的元素都存在这个链表中(这种方式叫拉链法来解决碰撞)
明白哈希表的实现原理,知道哈希函数和哈希碰撞;
实际中哈希表、HashMap、HashSet、 Hashtable等,在语言原生都是已经实现好了的;
如果碰撞的越来越多，链表会越来越长，它的查询时间复杂度就变成了O(n)，哈希表设计的好会避免很多哈希碰撞，我们可以认为它的查询时间复杂度是O(1)。
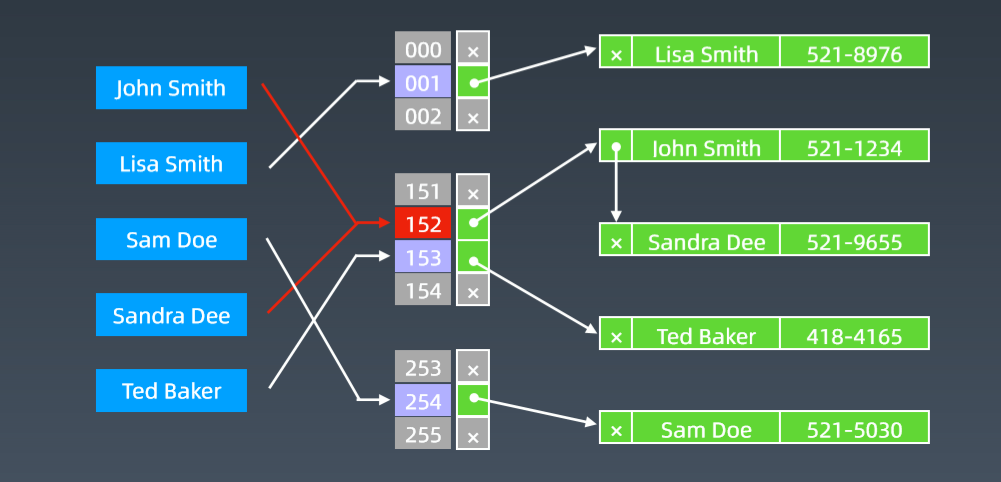
常用的散列冲突解决方法有两类：
- 开放寻址法（open addressing）
- 链表法（chaining）
1.3.1 开放寻址法
开放寻址法的核心思想是，如果出现了散列冲突，就重新探测一个空闲位置，将其插入。如何重新探测新的位置：
① 线性探测（Linear Probing）
当我们往散列表中插入数据时，如果某个数据经过散列函数散列之后，存储位置已经被占用了，我们就从当前位置开始，依次往后查找，看是否有空闲位置，直到找到为止。
下图黄色的色块表示空闲位置，橙色的色块表示已经存储了数据。
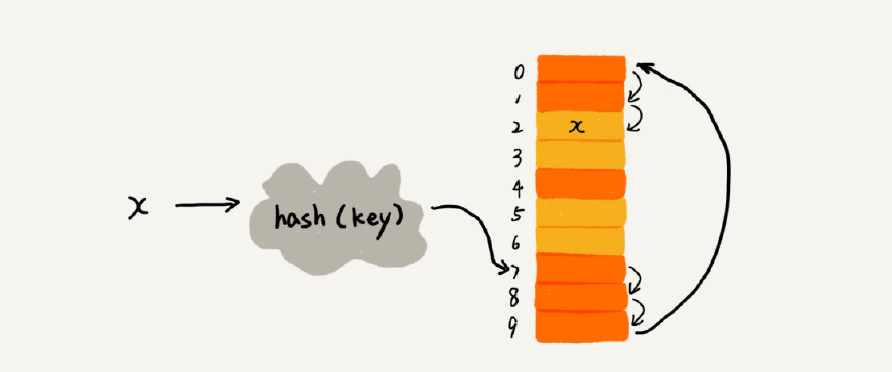
从图中可以看出，散列表的大小为 10，在元素 x 插入散列表之前，已经 6 个元素插入到散列表中。x 经过 Hash 算法之后，被散列到位置下标为 7 的位置，但是这个位置已经有数据了，所以就产生了冲突。于是我们就顺序地往后一个一个找，看有没有空闲的位置，遍历到尾部都没有找到空闲的位置，于是我们再从表头开始找，直到找到空闲位置 2，于是将其插入到这个位置。
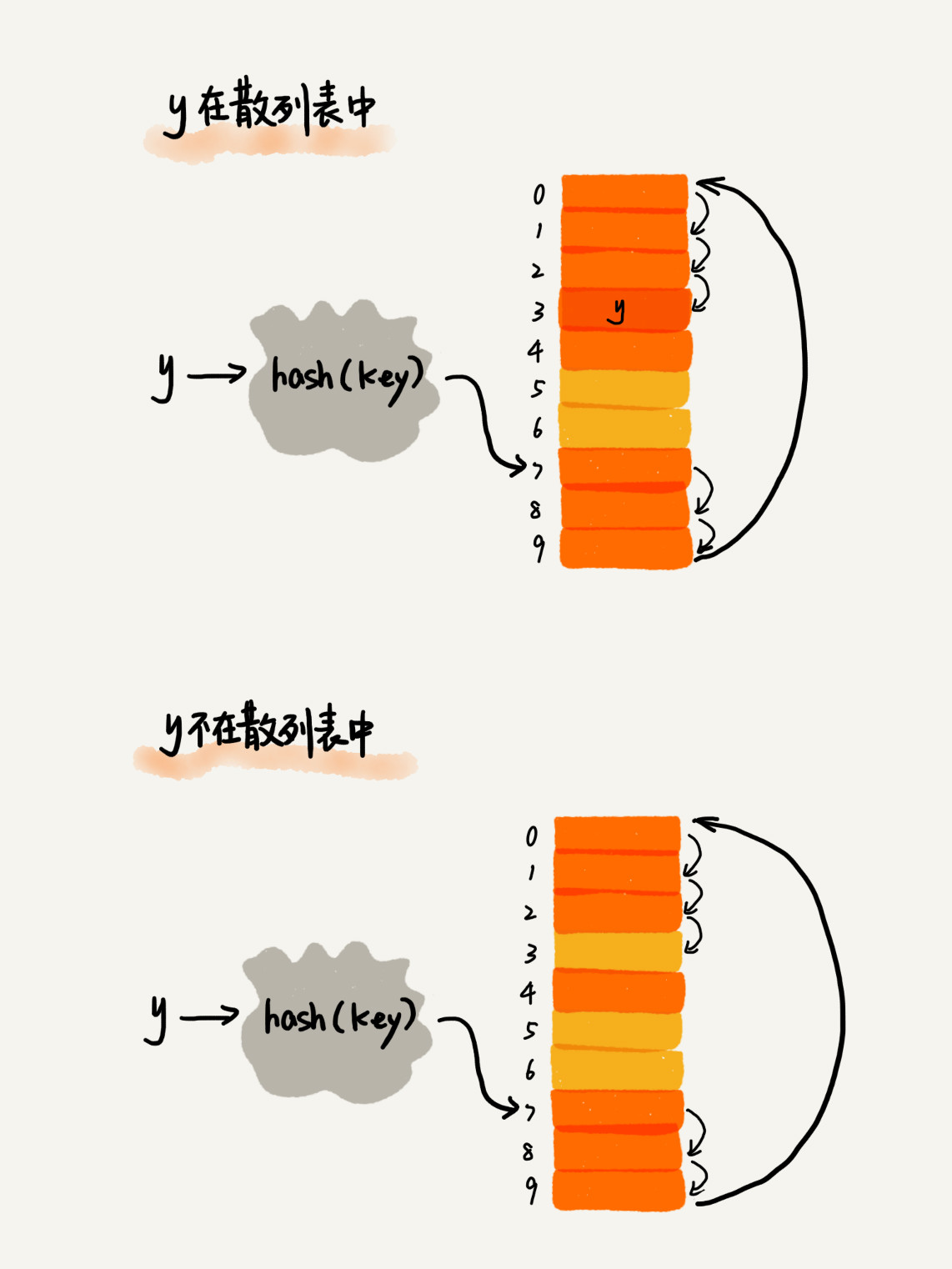
在散列表中查找元素的过程有点儿类似插入过程。我们通过散列函数求出要查找元素的键值对应的散列值，然后比较数组中下标为散列值的元素和要查找的元素。
如果相等，则说明就是我们要找的元素；否则就顺序往后依次查找。如果遍历到数组中的空闲位置，还没有找到，就说明要查找的元素并没有在散列表中。
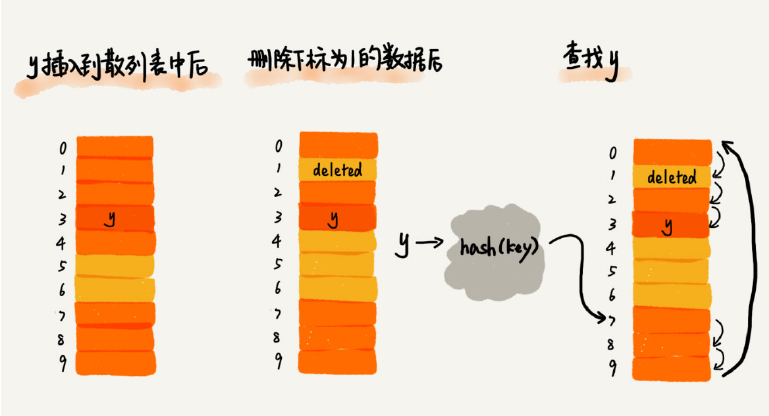
散列表跟数组一样，不仅支持插入、查找操作，还支持删除操作。对于使用线性探测法解决冲突的散列表，删除操作稍微有些特别。我们不能单纯地把要删除的元素设置为空。
在查找时，一旦通过线性探测方法，找到一个空闲位置，我们就可以认定散列表中存在这个数据。但是，如果这个空闲位置是我们后来删除的，就会导致原来的查找算法失效。本来存在的数据，会被认定为不存在。这个问题如何解决呢？
我们可以将删除的元素，特殊标记为 deleted。当线性探测查找的时候，遇到标记为 deleted 的空间，并不是停下来，而是继续往下探测。
当散列表中插入的数据越来越多时，散列冲突发生的可能性就会越来越大，空闲位置会越来越少，线性探测的时间就会越来越久。极端情况下，我们可能需要探测整个散列表，所以最坏情况下的时间复杂度为 O(n)。同理，在删除和查找时，也有可能会线性探测整张散列表，才能找到要查找或者删除的数据。
② 二次探测（Quadratic probing）
二次探测，跟线性探测很像，线性探测每次探测的步长是 1，那它探测的下标序列就是 hash(key)+0，hash(key)+1，hash(key)+2……而二次探测探测的步长就变成了原来的“二次方”，也就是说，它探测的下标
序列就是 hash(key)+0，hash(key)+12，hash(key)+22……
③ 双重散列（Double hashing）
所谓双重散列，意思就是不仅要使用一个散列函数。我们使用一组散列函数 hash1(key)，hash2(key)，hash3(key)……我们先用第一个散列函数，如果计算得到的存储位置已经被占用，再用第二个散列函数，依
次类推，直到找到空闲的存储位置。
不管采用哪种探测方法，当散列表中空闲位置不多的时候，散列冲突的概率就会大大提高。为了尽可能保证散列表的操作效率，一般情况下，我们会尽可能保证散列表中有一定比例的空闲槽位。我们用装载因子（load factor）来表示空位的多少。
装载因子的计算公式是：
散列表的装载因子 = 填入表中的元素个数 / 散列表的长度
装载因子越大，说明空闲位置越少，冲突越多，散列表的性能会下降。
1.3.2 链表法
链表法是一种更加常用的散列冲突解决办法，相比开放寻址法，它要简单很多。我们来看这个图，在散列表中，每个“桶（bucket）”或者“槽（slot）”会对应一条链表，所有散列值相同的元素我们都放到相同槽位对应的链表中。
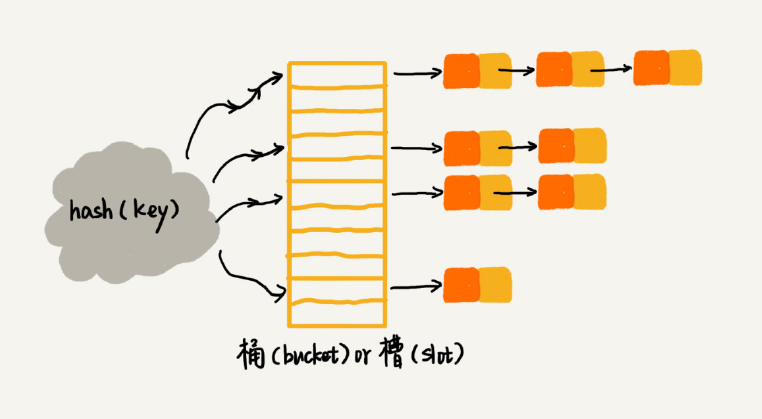
当插入的时候，我们只需要通过散列函数计算出对应的散列槽位，将其插入到对应链表中即可，所以插入的时间复杂度是 O(1)。当查找、删除一个元素时，我们同样通过散列函数计算出对应的槽，然后遍历
链表查找或者删除。那查找或删除操作的时间复杂度是多少呢？
实际上，这两个操作的时间复杂度跟链表的长度 k 成正比，也就是 O(k)。对于散列比较均匀的散列函数来说，理论上讲，k=n/m，其中 n 表示散列中数据的个数，m 表示散列表中“槽”的个数。
1.4 复杂度分析
哈希表的时间空间复杂度： 查询、 添加、 删除都是 O(1) ，最坏情况是哈希函数选的不好或者它的整个size太小了就会导致经常发生冲突，一冲突就变成链表了，很多时候它的复杂度就退化成 O(n)了。
1.5 应用
Word 文档中单词拼写检查功能是如何实现的？
常用的英文单词有 20 万个左右，假设单词的平均长度是 10 个字母，平均一个单词占用 10 个字节的内存空间，那 20 万英文单词大约占 2MB 的存储空间，就算放大 10 倍也就是 20MB。
对于现在的计算机来说，这个大小完全可以放在内存里面。所以我们可以用散列表来存储整个英文单词词典。
当用户输入某个英文单词时，我们拿用户输入的单词去散列表中查找。如果查到，则说明拼写正确；如果没有查到，则说明拼写可能有误，给予提示。借助散列表这种数据结构，我们就可以轻松实现快速判断是否存在拼写错误。
1. 假设我们有 10 万条 URL 访问日志，如何按照访问次数给 URL 排序？
遍历 10 万条数据，以 URL 为 key，访问次数为 value，存入散列表，同时记录下访问次数的最大值 K，时间复杂度 O(N)。
如果 K 不是很大，可以使用桶排序，时间复杂度 O(N)。如果 K 非常大（比如大于 10 万），就使用快速排序，复杂度 O(NlogN)。
2. 有两个字符串数组，每个数组大约有 10 万条字符串，如何快速找出两个数组中相同的字符串？
以第一个字符串数组构建散列表，key 为字符串，value 为出现次数。再遍历第二个字符串数组，以字符串为 key 在散列表中查找，如果 value 大于零，说明存在相同字符串。时间复杂度 O(N)。
1.6 工程实践
在工程中就不再用哈希表了，经常抽象出来使用。比如Java中Map和Set
电话号码簿、 用户信息表、 缓存（LRU Cache）、 键值对存储（Redis）
在Java - Code：
Map：key-value对，key不重复，值value可以重复；
- new HashMap() / new TreeMap()
- map.set(key,value)
- map.get(key)
- map.has(key)
- map.size()
- map.clear()
Set：不重复元素的集合，没有键值对，而是一个单个的元素，单个元素是不重复的。
- new HashSet() / new TreeSet()
- set.add(value)
- set.delete(value)
- set.hash(value)
在python中 dict或者json，set在python中就是set。
Java Map文档 HashMap、 Hashtable、 ConcurrentHashMap
Java Set文档 TreeSet、 HashSet、 ConcurrentSkipListSet、 CopyOnWriteArraySet、 EnumSet、 JobStateReasons、 LinkedHashSet
List VS Map VS Set
List和Map是抽象性和解释性;
list_x = [1,2,3,4] 它的实现可以是数组也可以是链表,关键是它是可以重复的;
插入是O(1)的时间复杂度,查找是O(n);
map_x = {
'jack':100,
'张三':80,
'kris':90,
...
}
map是一种映射;
Set抽象接口，它背后的实现类千差万别
set_x = {'jack','kris','andy'}
set_y = set(['jack','kris','jack'])
集合,跟map比较相似,可把它看做map的key;集合不能有重复,可看做去重后的list
集合的实现背后有两种: 哈希表或者树 二叉树的形式来实现;
查找是O(1)时间复杂度或者Logn, 它比List的效率要高;
1.7 HashSet和HashMap源代码的实现
HashMap vs TreeMap
HashSet vs TreeSet
hashtable vs binary-search
以上三种跟List、Map和Set能够达到的目的是一样的, 只不过里边的元素排列和存储的方式不同;
HashMap/HashSet/hashtable用的是hash表来存储, 查询时时间复杂度是O(1), 是乱序的;
TreeMap/TreeSet/binary-search用的是二叉树来存储, 时间复杂度是Log(n), 都是排好序的(有序); TreeMap、 TreeSet等都是用二叉搜索树即红黑树来实现，严格平衡的红黑树。
HashSet的实现
public class HashSet<E> extends AbstractSet<E> implements Set<E>, Cloneable, java.io.Serializable
public HashSet() {
map = new HashMap<>(); //HashSet它的背后就是建了一个HashMap，
}
public boolean add(E e) {
return map.put(e, PRESENT)==null; //add方法就是把这个元素放到它的key的位置上去，它的value叫 PRESENT，//private static final Object PRESENT = new Object();// Dummy value to associate with an Object in the backing Map
//present就是它新建了一个叫dummy value，随便用了一个object作为占位使用，表示我在场。
}
public boolean remove(Object o) { return map.remove(o)==PRESENT; } //remove也是从hashmap中移除。
HashSet它背后就是嫁接在HashMap上。HashSet每次都存一个present，岂不是浪费内存空间。
HashMap的实现
它的node分为 HashNode和TreeNode这两种。
put、 putVal
get
