数据结构-04 |栈 |队列

概述

栈Stack |队列Queue| 双端队列Deque| 优先队列PriorityQueue

堆栈和队列特点：
1. Stack - First In Last Out(FILO) 先入后出，先进来的被压入栈底
    .Array or Linked List
2. Queue - First In First Out(FIFO) 排队时先来先出
    .Array or Doubly Linked List

1. Java中栈的实现API

在Java中，用Deque可以实现Stack的功能：

把元素压栈：push(E)/addFirst(E)；
把栈顶的元素“弹出”：pop(E)/removeFirst()；
取栈顶元素但不弹出：peek(E)/peekFirst()。

为什么Java的集合类没有单独的Stack接口呢？因为有个遗留类名字就叫Stack，出于兼容性考虑，所以没办法创建Stack接口，只能用Deque接口来“模拟”一个Stack了。不要使用遗留类Stack

当我们把Deque作为Stack使用时，注意只调用push()/pop()/peek()方法，不要调用addFirst()/removeFirst()/peekFirst()方法，这样代码更加清晰。

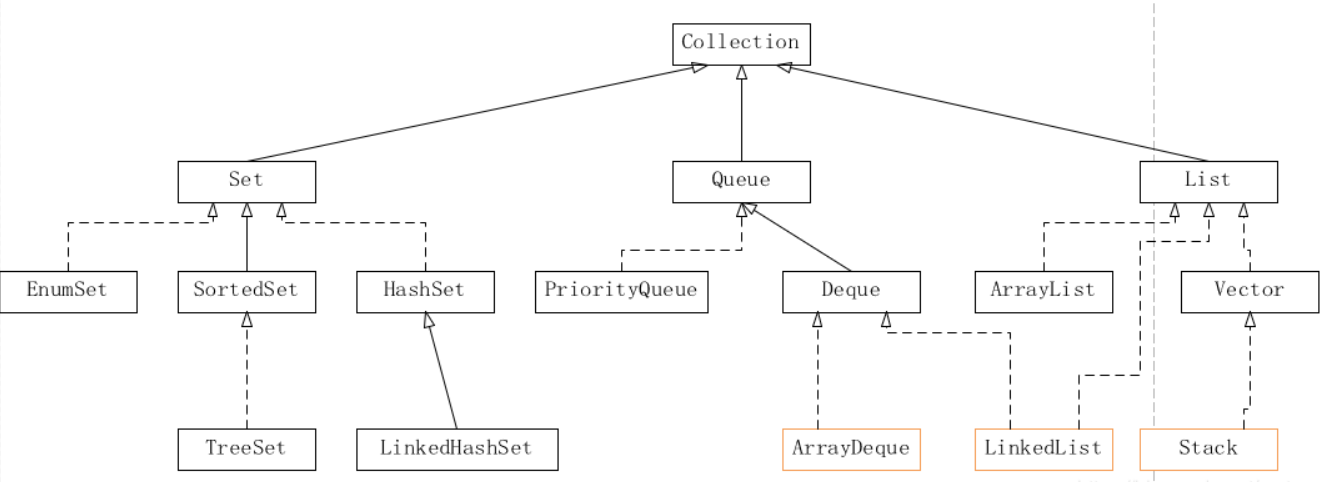
Stack，ArrayDeque，LinkedList都可以作为栈使用：

由继承树看出，三者都是Collection的间接实现类。 ArrayDeque实现Deque接口，Stack继承于Vector，LinkedList实现Deque与List接口。

区别

底层数据存储方式：

	存储方式
Stack	长度为10的数组
ArrayDeque	长度为16的数组
LinkedList	链表

存储方式

Stack

长度为10的数组

ArrayDeque

长度为16的数组

LinkedList

链表

线程安全

	线程安全
Stack	线程同步
ArrayDeque	线程不同步
LinkedList	线程不同步

使用Collections工具类中synchronizedXxx() 可以将线程不同步的ArrayDeque以及LinkedList转换成线程同步。

性能选项

通常情况下，不推荐使用Vector以及其子类Stack （它们实现了线程同步的功能，所以性能比较差）；

　　频繁的插入、删除操作，未知的初始数据量：LinkedList ；

　　频繁的随机访问操作：ArrayDeque

另一个区别是：LinkedList支持null元素，而ArrayDeque不支持。

2. Java中Queue队列的API

队列Queue实现了一个先进先出（FIFO）的数据结构：

通过add()/offer()方法将元素添加到队尾；
通过remove()/poll()从队首获取元素并删除；
通过element()/peek()从队首获取元素但不删除。

要避免把null添加到队列。

// 这是一个List:  List<String> list = new LinkedList<>();
// 这是一个Queue: Queue<String> queue = new LinkedList<>();
LinkedList即实现了List接口，又实现了Queue接口，但是，在使用的时候，如果我们把它当作List，就获取List的引用，如果我们把它当作Queue，就获取Queue的引用
 ArrayDeque也实现了Deque接口（Deque接口继承了Queue接口）

3. 双端队列Deque的API

Deque是一个接口，它的实现类有ArrayDeque和LinkedList （LinkedList真是一个全能选手，它即是List，又是Queue，还是Deque）

// 不推荐的写法: LinkedList<String> deque = new LinkedList<>();
// 推荐的写法：  Deque<String> deque = new LinkedList<>(); （面向抽象编程的一个原则就是：尽量持有接口，而不是具体的实现类。）

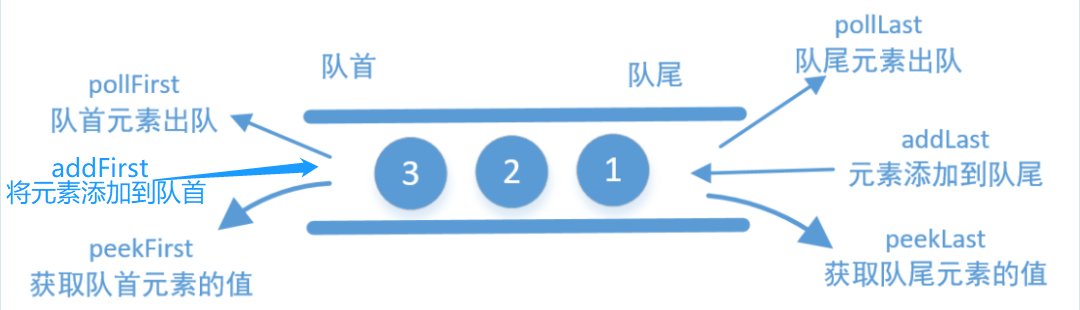
将元素添加到队首： addFirst()即push() / offerFirst()； 　　
将元素添加到队尾：addLast()即add() / offerLast() 即offer()

从队首获取元素并删除：removeFirst()即remove() pop() / pollFirst() 即poll() 　
从队尾获取元素并删除：removeLast()/ pollLast()；

从队首获取元素但不删除：getFirst()/ peekFirst() 即peek() 　　
从队尾获取元素但不删除：getLast()/ peekLast()；

总是调用xxxFirst()/xxxLast()以便与Queue的方法区分开；
避免把null添加到队列。

如果直接写deque.offer()，我们就需要思考，offer()实际上是offerLast()，我们明确地写上offerLast()，不需要思考就能一眼看出这是添加到队尾。

因此，使用Deque，推荐总是明确调用offerLast() /offerFirst()或者pollFirst() /pollLast()方法。

4. 优先队列PriorityQueue的API

Queue<String> q = new PriorityQueue<>();

PriorityQueue和Queue的区别在于，它的出队顺序与元素的优先级有关，对PriorityQueue调用remove()或poll()方法，返回的总是优先级最高的元素。

要使用PriorityQueue，我们就必须给每个元素定义“优先级”。

PriorityQueue实现了一个优先队列：从队首获取元素时，总是获取优先级最高的元素。

PriorityQueue默认按元素比较的顺序排序（必须实现Comparable接口），也可以通过Comparator自定义排序算法（元素就不必实现Comparable接口）。

放入PriorityQueue的元素，必须实现Comparable接口，PriorityQueue会根据元素的排序顺序决定出队的优先级。

如果我们要放入的元素并没有实现Comparable接口怎么办？PriorityQueue允许我们提供一个Comparator对象来判断两个元素的顺序。

1. 栈Stack

Stack中文名可叫堆栈，不能叫堆，堆是heap

手写栈堆比较少了，很多语言在标准库都实现了。

1.1 概念与特性

后进先出，先进后出，这就是典型的“栈”结构。

从栈的操作特性上来看，栈是一种“操作受限”的线性表，只允许在一端插入和删除数据。从功能上来说，数组或链表可以替代栈，但特定的数据结构是对特定场景的抽象，而且，数组或链表暴露了太多的操作接口，操作上的确灵活自由，但使用时就比较不可控，自然也就更容易出错。

当某个数据集合只涉及在一端插入和删除数据，并且满足后进先出、先进后出的特性，我们就应该首选“栈”这种数据结构。

最近相关性《====》栈现实中的洋葱，一层层，反应在工程中都具有从外而内 或者由内而外这种逐渐扩散，且它的最外层和最外层是一对，最内层和最内层是一对可叫最近相关性。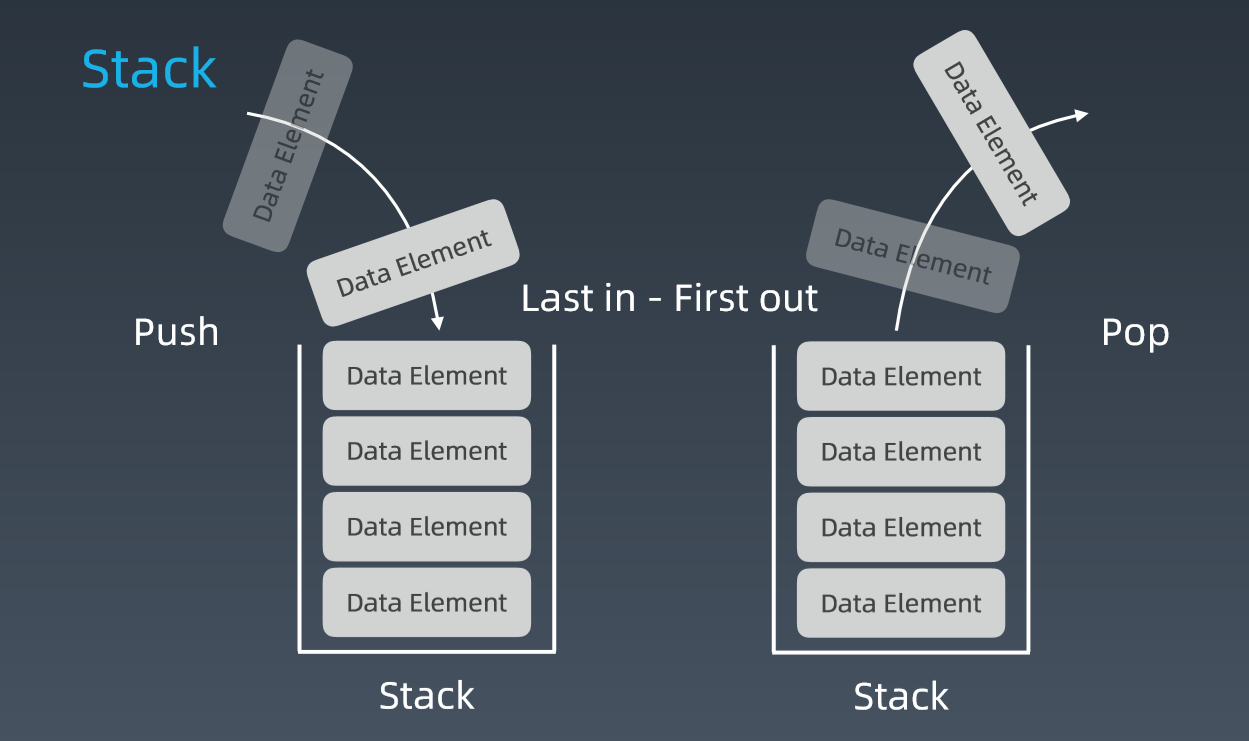

栈：查询 O(n)，平均情况，要看它栈中栈底的元素，要清空了才能看到。

插入和删除它的栈顶元素只需要一次性操作，时间复杂度是O(1)。

1.2 如何实现一个“栈”？

从栈的定义里，栈主要包含两个操作，入栈和出栈，即在栈顶插入一个数据和从栈顶删除一个数据。

自定义一个栈既可以用数组来实现，也可以用链表来实现。用数组实现的栈，叫作顺序栈，用链表实现的栈，叫作链式栈。

// 基于数组实现的顺序栈
public class ArrayStack {
    private String[] items;  // 数组
    private int count;       // 栈中元素个数
    private int n;           // 栈的大小
    // 初始化数组，申请一个大小为 n 的数组空间
    public ArrayStack(int n) {
        this.items = new String[n];
        this.n = n;
        this.count = 0;
    }
    // 入栈操作
    public boolean push(String item) {
        // 数组空间不够了，直接返回 false，入栈失败。
        if (count == n) return false;
        // 将 item 放到下标为 count 的位置，并且 count 加一
        items[count] = item;
        ++count;
        return true;
    }
    // 出栈操作
    public String pop() {
        // 栈为空，则直接返回 null
        if (count == 0) return null;
        // 返回下标为 count-1 的数组元素，并且栈中元素个数 count 减一
        String tmp = items[count - 1];
        --count;
        return tmp;
    }
}

View Code

不管是顺序栈还是链式栈，存储数据只需要一个大小为 n 的数组就够了。在入栈和出栈过程中，只需要一两个临时变量存储空间，所以空间复杂度是 O(1)。（空间复杂度是指除了原本的数据存储空间外，算法运行还需要额外的存储空间，这里存储数据需要一个大小为 n 的数组，并不是说空间复杂度就是 O(n) ）

不管是顺序栈还是链式栈，入栈、出栈只涉及栈顶个别数据的操作，时间复杂度都是 O(1)。

在Java中，用Deque可以实现Stack的功能：

把元素压栈：push(E)/addFirst(E)；
把栈顶的元素“弹出”：pop(E)/removeFirst()；
取栈顶元素但不弹出：peek(E)/peekFirst()。

当我们把Deque作为Stack使用时，注意只调用push()/pop()/peek()方法，不要调用addFirst()/removeFirst()/peekFirst()方法，这样代码更加清晰。

1.3 支持动态扩容的顺序栈

刚才那个基于数组实现的栈，是一个固定大小的栈，也就是说，在初始化栈时需要事先指定栈的大小。当栈满之后，就无法再往栈里添加数据了。尽管链式栈的大小不受限，但要存储 next 指针，内存消耗相对

较多。那如何基于数组实现一个可以支持动态扩容的栈呢？

在数组中当数组空间不够时，我们就重新申请一块更大的内存，将原来数组中数据统统拷贝过去。这样就实现了一个支持动态扩容的数组。

所以，如果要实现一个支持动态扩容的栈，只需要底层依赖一个支持动态扩容的数组就可以了。当栈满了之后，我们就申请一个更大的数组，将原来的数据搬移到新数组中。

实际上，支持动态扩容的顺序栈，平时开发中并不常用到。重点是复杂度分析。下面分析一下支持动态扩容的顺序栈的入栈、出栈操作的时间复杂度。

对于出栈操作来说，不会涉及内存的重新申请和数据的搬移，所以出栈的时间复杂度仍然是 O(1)。但是，对于入栈操作来说，情况就不一样了。当栈中有空闲空间时，入栈操作的时间复杂度为 O(1)。但当空间

不够时，就需要重新申请内存和数据搬移，所以时间复杂度就变成了 O(n)。

也就是说，对于入栈操作来说，好情况时间复杂度是 O(1)，坏情况时间复杂度是 O(n)。那平均情况下的时间复杂度又是多少呢？用到了摊还分析法，这个入栈操作的平均情况下的时间复杂度可以用摊还分析法来分析。为了分析的方便，需要事先做一些假设和定义：

栈空间不够时，我们重新申请一个是原来大小两倍的数组；
为了简化分析，假设只有入栈操作没有出栈操作；
定义不涉及内存搬移的入栈操作为 simple-push 操作，时间复杂度为 O(1)。

如果当前栈大小为 K，并且已满，当再有新的数据要入栈时，就需要重新申请 2 倍大小的内存，并且做 K 个数据的搬移操作，然后再入栈。但是，接下来的 K-1 次入栈操作，都不需要再重新申请内存和搬移数

据，所以这 K-1 次入栈操作都只需要一个 simple-push 操作就可以完成。

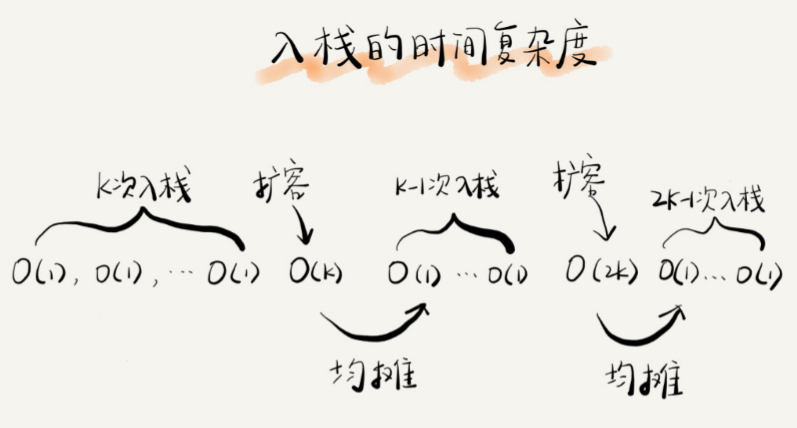
这 K 次入栈操作，总共涉及了 K 个数据的搬移，以及 K 次 simple-push 操作。将 K 个数据搬移均摊到 K 次入栈操作，那每个入栈操作只需要一个数据搬移和一个 simple-push 操作。以此类推，入栈操作的均摊

时间复杂度就为 O(1)。

通过这个例子的实战分析，也印证均摊时间复杂度一般都等于好情况时间复杂度。因为在大部分情况下，入栈操作的时间复杂度 O 都是 O(1)，只有在个别时刻才会退化为 O(n)，所以把耗时多的

入栈操作的时间均摊到其他入栈操作上，平均情况下的耗时就接近 O(1)。

1.3 栈的应用

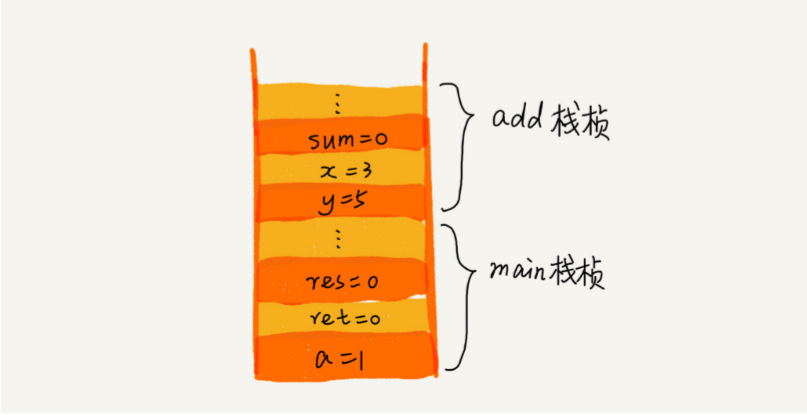
① 栈在函数调用中的应用，经典的一个应用场景就是函数调用栈。

操作系统给每个线程分配了一块独立的内存空间，这块内存被组织成“栈”这种结构, 用来存储函数调用时的临时变量。每进入一个函数，就会将临时变量作为一个栈帧入栈，当被调用函数执行完成，返回之后，将这个函数对应的栈帧出栈。

    public static void main(String[] args) {
        int a = 1;
        int ret = 0;
        int res = 0;
        ret = add(3, 5);
        res = a + ret;
        System.out.println(res); // 9

    }

    private static int add(int x, int y) {
        int sum = 0;
        sum = x + y;
        return sum;
    }

View Code

② 栈在表达式求值中的应用

我们再来看栈的另一个常见的应用场景，编译器如何利用栈来实现表达式求值。

为了方便解释，我将算术表达式简化为只包含加减乘除四则运算，比如：34+13*9+44-12/3。

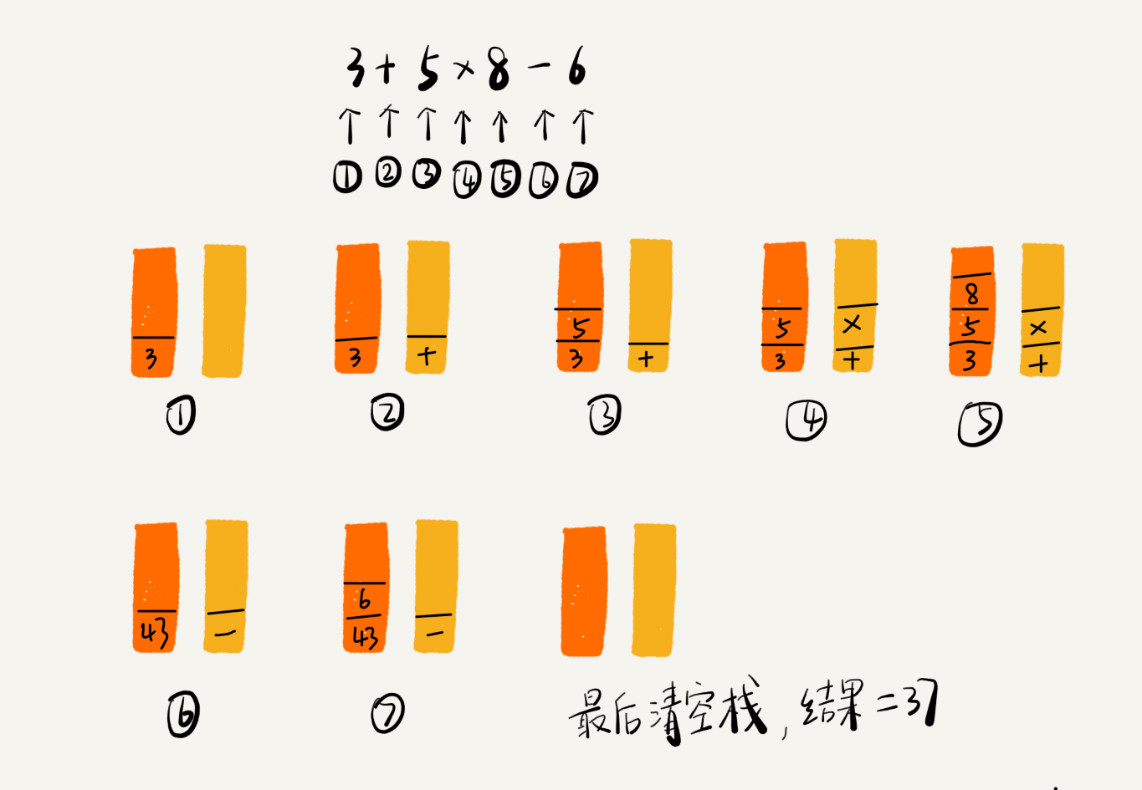
③ 栈在括号匹配中的应用

假设表达式中只包含三种括号，圆括号 ()、方括号 [] 和花括号{}，并且它们可以任意嵌套。比如，{[{}]}或 [{()}([])] 等都为合法格式，而{[}()] 或 [({)] 为不合法的格式。那我现在给你一个包含三种括号的表达式字符串，如何检查它是否合法呢？

这里也可以用栈来解决。我们用栈来保存未匹配的左括号，从左到右依次扫描字符串。当扫描到左括号时，则将其压入栈中；当扫描到右括号时，从栈顶取出一个左括号。如果能够匹配，比如“(”跟“)”匹配，“[”跟“]”匹配，“{”跟“}”匹配，则继续扫描剩下的字符串。如果扫描的过程中，遇到不能配对的右括号，或者栈中没有数据，则说明为非法格式。

当所有的括号都扫描完成之后，如果栈为空，则说明字符串为合法格式；否则，说明有未匹配的左括号，为非法格式。

④ 基于栈实现浏览器的前进和后退功能

当你依次访问完一串页面 a-b-c 之后，点击浏览器的后退按钮，就可以查看之前浏览过的页面 b 和 a。当你后退到页面 a，点击前进按钮，就可以重新查看页面 b 和 c。但是，如果你后退到页面 b 后，点击了新的页面 d，那就无法再通过前进、后退功能查看页面 c 了。

用两个栈就可以非常完美地解决这个问题。

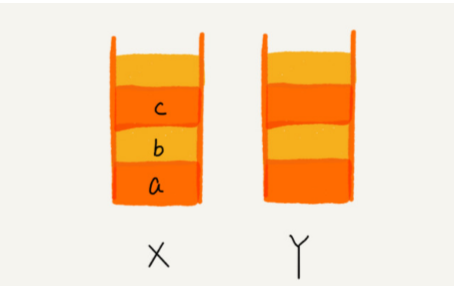
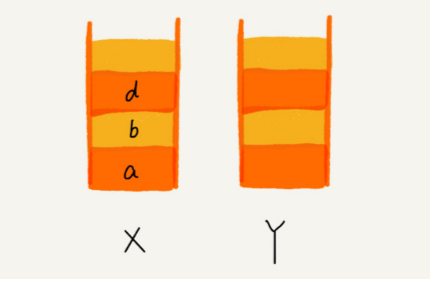
我们使用两个栈，X 和 Y，我们把首次浏览的页面依次压入栈 X，当点击后退按钮时，再依次从栈 X 中出栈，并将出栈的数据依次放入栈 Y。当我们点击前进按钮时，我们依次从栈 Y 中取出数据，放入栈 X 中。当栈 X 中没有数据时，那就说明没有页面可以继续后退浏览了。当栈 Y 中没有数据，那就说明没有页面可以点击前进按钮浏览了。

比如顺序查看了 a，b，c 三个页面，然后依次把 a，b，c 压入栈，这个时候，两个栈的数据就是这个样子：

当通过浏览器的后退按钮，从页面 c 后退到页面 a 之后，我们就依次把 c 和 b 从栈 X 中弹出，并且依次放入到栈 Y。这个时候，两个栈的数据就是这个样子：

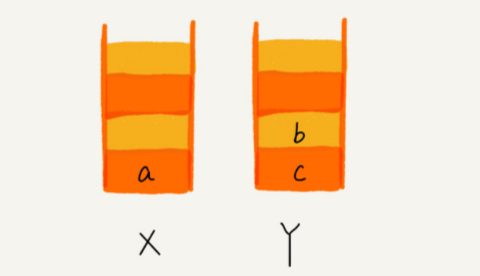
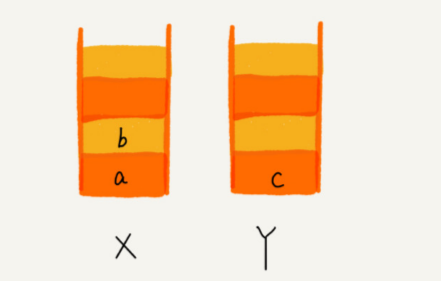
这时你又想看页面 b，于是你又点击前进按钮回到 b 页面，我们就把 b 再从栈 Y 中出栈，放入栈 X 中。此时两个栈的数据是这个样子：

这时，你通过页面 b 又跳转到新的页面 d 了，页面 c 就无法再通过前进、后退按钮重复查看了，所以需要清空栈 Y。此时两个栈的数据这个样子：

栈的应用场景

1) 子程序的调用：在跳往子程序前，会先将下个指令的地址存到堆栈中，直到子程序执行完后再将地址取出，以回到原来的程序中。

2) 处理递归调用：和子程序的调用类似，只是除了储存下一个指令的地址外，也将参数、区域变量等数据存入堆栈中。

3) 表达式的转换与求值(实际解决)。

4) 二叉树的遍历。

5) 图形的深度优先(depth一first)搜索法。

思考

1. 为什么函数调用要用“栈”来保存临时变量呢？用其他数据结构不行吗？

其实，我们不一定非要用栈来保存临时变量，只不过如果这个函数调用符合后进先出的特性，用栈这种数据结构来实现，是顺理成章的选择。

从调用函数进入被调用函数，对于数据来说，变化的是什么呢？是作用域。所以根本上，只要能保证每进入一个新的函数，都是一个新的作用域就可以。而要实现这个，用栈就非常方便。在进入被调用函数的

时候，分配一段栈空间给这个函数的变量，在函数结束的时候，将栈顶复位，正好回到调用函数的作用域内。

2. 内存中的堆栈和数据结构堆栈不是一个概念，可以说内存中的堆栈是真实存在的物理区，数据结构中的堆栈是抽象的数据存储结构。
内存空间在逻辑上分为三部分：代码区、静态数据区和动态数据区，动态数据区又分为栈区和堆区。

代码区：存储方法体的二进制代码。高级调度（作业调度）、中级调度（内存调度）、低级调度（进程调度）控制代码区执行代码的切换。
静态数据区：存储全局变量、静态变量、常量，常量包括final修饰的常量和String常量。系统自动分配和回收。
栈区：存储运行方法的形参、局部变量、返回值。由系统自动分配和回收。
堆区：new一个对象的引用或地址存储在栈区，指向该对象存储在堆区中的真实数据。

2. 队列Queue

2.1 概念和特性

队列，排队，先来先出，依次排队。一头进另外一头出。

队列，先来后到，公平性，队列

我们知道，栈只支持两个基本操作：入栈 push()和出栈 pop()。队列跟栈非常相似，支持的操作也很有限，最基本的操作也是两个：

　　入队 enqueue()，放一个数据到队列尾部；出队 dequeue()，从队列头部取一个元素。所以，队列跟栈一样，也是一种操作受限的线性表数据结构。

作为一种非常基础的数据结构，队列的应用也非常广泛，特别是一些具有某些额外特性的队列，比如循环队列、阻塞队列、并发队列。它们在很多偏底层系统、框架、中间件的开发中，起着关键性的作用。比如高性能队列 Disruptor、Linux 环形缓存，都用到了循环并发队列；Java concurrent 并发包利用 ArrayBlockingQueue 来实现公平锁等。

栈：查询 O(n)，平均情况，要看它栈中栈底的元素，要清空了才能看到。 插入和删除它的栈顶元素只需要一次性操作，时间复杂度是O(1)。

队列：与栈类似，查询是O(n），插入和删除是O(1）。

查询操作O(n)，因为它是元素无序的，就必须把这个数据结构遍历一遍，把它想象成排队买票，先来的先买，后来的人只能站末尾，不允许插队。先进者先出，这就是典型的“队列”。

2.2 顺序队列和链式队列

队列跟栈一样，也是一种抽象的数据结构。它具有先进先出的特性，支持在队尾插入元素，在队头删除元素，如何实现一个队列？

跟栈一样，队列可以用数组来实现，也可以用链表来实现。用数组实现的栈叫作顺序栈，用链表实现的栈叫作链式栈。

同样，用数组实现的队列叫作顺序队列，用链表实现的队列叫作链式队列。

对于栈来说，我们只需要一个栈顶指针就可以了。但是队列需要两个指针：一个是 head 指针，指向队头；一个是 tail 指针，指向队尾。

用数组实现一个queue：

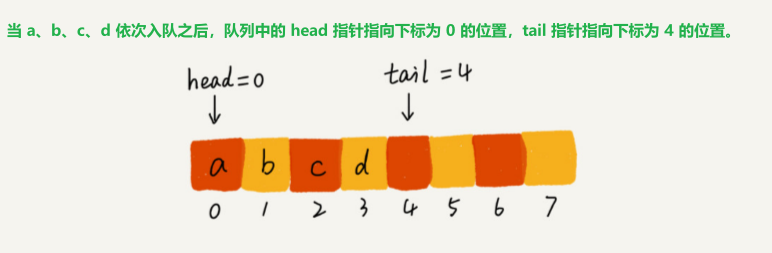
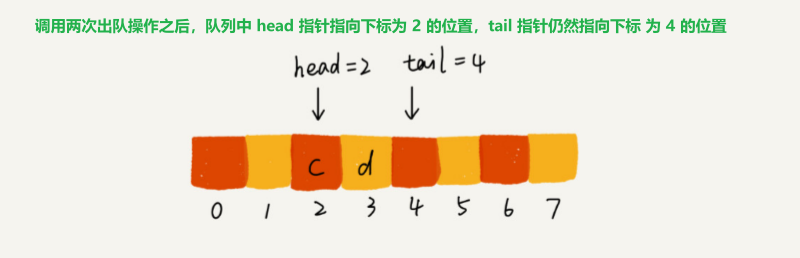
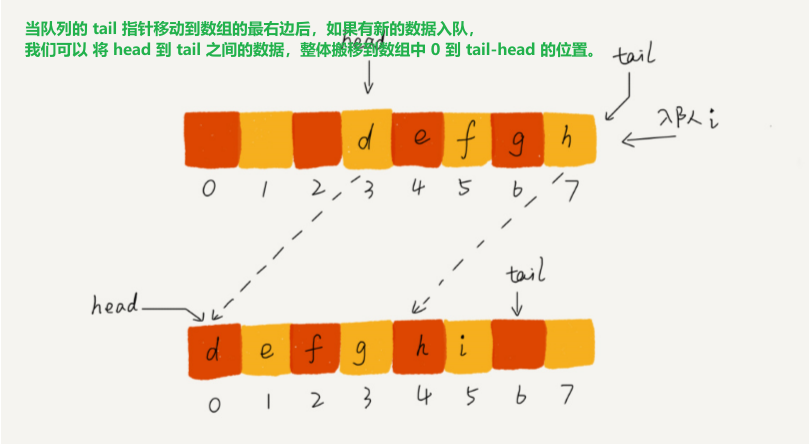
具体实现代码如下：

/**
 * 用数组实现的队列
 * 一个问题:
 * 随着不停地进行入队、出队操作，head 和 tail 都会持续往后移动。当 tail 移动到最右边，即使数组中还有空闲空间，也无法继续往队列中添加数据了
 * 解决办法:
 * 数据搬移: 每次出队操作都相当于删除数组下标为 O 的数据，要搬移整个队列中的数据，这样出队操作的时间复杂度就会从原来的 O(1) 变为 O(n)
 * 优化: 出队时可以不用搬移数据。如果没有空闲空间了，我们只需要在入队时，再集中触发一次数据的搬移操作。 出队函数 dequeue() 保持不变，改造一下入队函数 enqueue()
 * 队列的 tail 指针移动到数组的最右边后，如果有新的数据入队，就将 head 到 tail 之间的数据，整体搬移到数组中 0 到 tail-head 的位置。
 */

public class ArrayQueue {
    public static void main(String[] args) {
        ArrayQueue arrayQueue = new ArrayQueue(3);
        System.out.println(arrayQueue.enqueue("a"));
        System.out.println(arrayQueue.enqueue("b"));
        System.out.println(arrayQueue.enqueue("c"));

        arrayQueue.printAll();
        System.out.println("\n" + arrayQueue.dequeue("a"));

    }

    private String[] items;
    private int n = 0; //数组大小
    private int head = 0; //队头下标
    private int tail = 0; //队尾下标

    /**
     * 申请一个大小为nacity的数组
     */
    public ArrayQueue(int nacity) {
        items = new String[nacity];
        n = nacity;
    }
    /*     /* 入队 /*
    public boolean enqueue(String item) {
        if (tail == n) return false; //队列满了
        items[tail] = item; //放在队尾
        ++tail;
        return true;
    }*/

    /**
     * 入队 将item元素放入队尾
     */
    public boolean enqueue(String item) {
        //1. tail == n 队列已满
        if (tail == n) {
            if (head == 0) return false; //tail == 0 && head == 0 表整个队列已满
            //数据搬移
            for (int i = head; i < tail; i++) {
                items[i - head] = items[i];
            }
            //搬完之后重新更新head和tail
            tail -= head;
            head = 0;
        }
        //2. 队列未满
        items[tail] = item; //放在队尾
        ++tail;
        return true;
    }

    /**
     * 出队 , 会导致类似数组删除操作中 -- 数据不连续
     */
    public String dequeue(String item) {
        if (head == tail) return null;
        String res = items[head];
        ++head;
        return res;

    }

    /**
     * 遍历整个队列
     */
    public void printAll() {
        for (int i = head; i < tail; i++) {
            System.out.print(items[i] + " ");
        }
    }
}

View Code

用链表实现的队列queue：

基于链表的实现，我们同样需要两个指针：head 指针和 tail 指针。它们分别指向链表的第一个结点和最后一个结点。入队时，tail->next= new_node, tail = tail->next；出队时，head = head->next

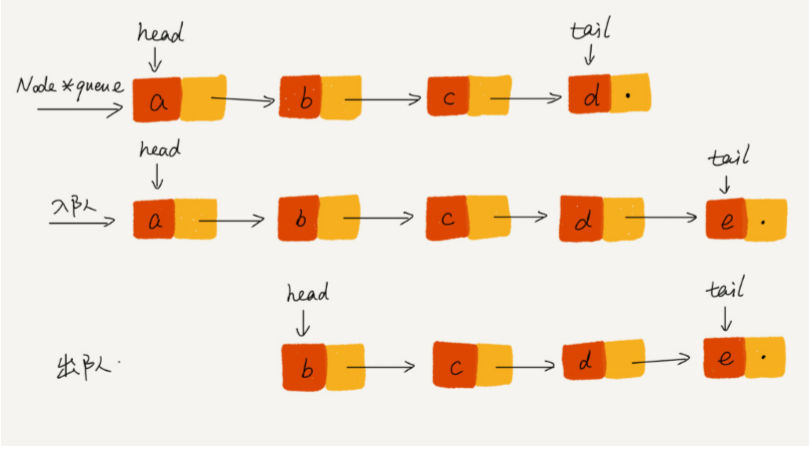
import com.leetcode.datastructure.linkedlist.ListNode;

/**
 * 基于链表实现的队列
 */
public class LinkedListQueue {
    public static void main(String[] args) {
        LinkedListQueue linkedListQueue = new LinkedListQueue();
        linkedListQueue.enqueue(1);
        linkedListQueue.enqueue(2);
        linkedListQueue.enqueue(3);
        linkedListQueue.printAll();
        linkedListQueue.dequeue();
        linkedListQueue.printAll();
    }

    private ListNode head = null;
    private ListNode tail = null;

    //入队
    public void enqueue(int value) {
        if (tail == null) {
            ListNode new_Node = new ListNode(value, null);
            head = new_Node;
            tail = new_Node;
        } else {
            tail.next = new ListNode(value, null);
            tail = tail.next;
        }
    }
    //出队
    public Integer dequeue() {
        if (head == null) return null;
        int value = head.data;
        head = head.next;
        if (head == null) {
            tail = null;
        }
        return value;
    }
    //遍历
    public void printAll() {
        ListNode p = head;
        while (p != null) {
            System.out.print(p.data + " ");
            p = p.next;
        }
        System.out.println();
    }
}

View Code

队列Queue实现了一个先进先出（FIFO）的数据结构：

通过add()/offer()方法将元素添加到队尾；
通过remove()/poll()从队首获取元素并删除；
通过element()/peek()从队首获取元素但不删除。

要避免把null添加到队列。

// 这是一个List:  List<String> list = new LinkedList<>();
// 这是一个Queue: Queue<String> queue = new LinkedList<>();
LinkedList即实现了List接口，又实现了Queue接口，但是，在使用的时候，如果我们把它当作List，就获取List的引用，如果我们把它当作Queue，就获取Queue的引用
 ArrayDeque也实现了Deque接口（Deque接口继承了Queue接口）

2.3 循环队列

循环队列是为了解决顺序队列在 tail == n 时，需要数据搬运操作的问题。

队列为空时可以根据 head == tail 来判断。

循环队列满时，tail 指针位置不存储数据，所以队满判断公式为：(tail + 1) % n = head。

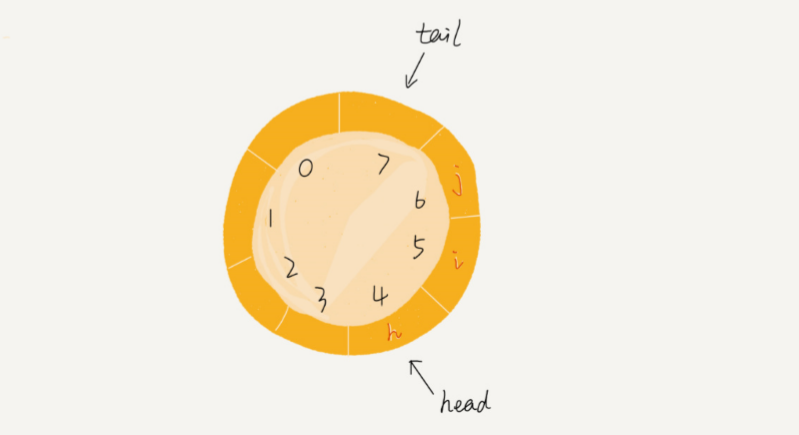
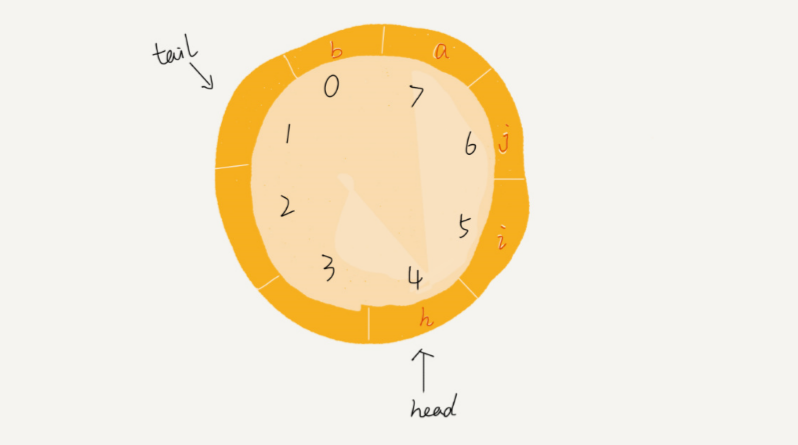
图中这个队列的大小为 8，当前 head=4，tail=7。当有一个新的元素 a 入队时，我们放入下标为 7 的位置。但这个时候，我们并不把 tail 更新为 8，而是将其在环中后移一位，到下标为 0 的位置。当再有一个

元素 b 入队时，我们将 b 放入下标为 0 的位置，然后 tail 加 1 更新为 1。所以，在 a，b 依次入队之后，循环队列中的元素就变成了下面的样子：

通过这样的方法，成功避免了数据搬移操作。但是循环队列的代码实现难度要比前面讲的非循环队列难多了。要想写出没有 bug 的循环队列的实现代码，最关键的是，确定好队空和队满的判定条件。

在用数组实现的非循环队列中，队满的判断条件是 tail == n，队空的判断条件是 head == tail。那针对循环队列，如何判断队空和队满呢？

　　队列为空的判断条件仍然是 head == tail。但队列满的判断条件就稍微有点复杂了，如下图：

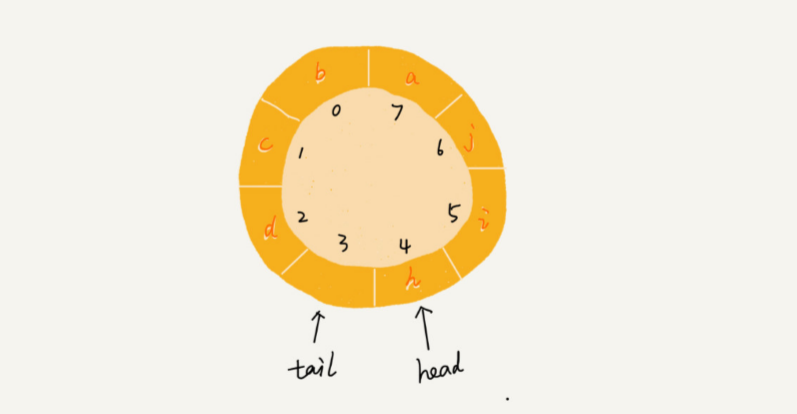
tail=3，head=4，n=8，所以总结一下规律就是：(3+1)%8=4。当队满时，( tail + 1 ) % n = head。你有没有发现，当队列满时，图中的 tail 指向的位置实际上是没有存储数据的。所以，循环队列会浪费一个数组的存储空间。

/**
 * 数组实现   循环队列(单)
 * 避免了数据搬移操作
 * 确定好队空和队满的判定条件
 * 数组实现 非循环队列，队满的判断条件是 tail == n，队空的判断条件是 head == tail
 *        循环队列 队列为空的判断条件仍然是 head == tail , 队满时的条件为 (tail+1)%n=head
 *               循环队列存的元素个数总是比他占用的存储空间少,队尾指针也需要占用一个位置
 *从 tail 进, head 出  先进先出
 *
 */
public class CircularQueue {

    public static void main(String[] args) {
        CircularQueue circularQueue = new CircularQueue(3);
        //入队测试
        System.out.println(circularQueue.enqueue("a"));
        System.out.println(circularQueue.enqueue("b"));
        System.out.println(circularQueue.enqueue("c"));

        //遍历循环队列
        circularQueue.printAll();
        //出队测试
        System.out.println("\n" + circularQueue.dequeue() );

    }

    private String[] items; //数组 items
    private int n = 0; //数组大小
    private int head = 0; //表队头下标
    private int tail = 0; //表队尾下标

    /** 申请一个大小为 nacity 的数组 */
    public CircularQueue(int nacity) {
        items = new String[nacity];
        n = nacity;
    }
    //入队
    public boolean enqueue(String item) {
        if ((tail + 1) % n == head ) return false;// (tail + 1) % n == head 即队列满了, tail指针也需要占用一个位置
        items[tail] = item;
        tail = (tail + 1) % n; //入队后 tail 往后 挪动
        return true;
    }

    //出队
    public String dequeue() {
        if (head == tail) return null; // head == tail 队列为空
        String ret = items[head];
        head = (head + 1) % n;
        return ret;
    }

    /**
     * 遍历循环队列
     */
    public void printAll() {
        for (int i = head; i % n != tail; i++) {
            System.out.print(items[i] + " ");
        }
    }

}

View Code

2.4 阻塞队列和并发队列

阻塞队列其实就是在队列基础上增加了阻塞操作。简单来说，就是在队列为空的时候，从队头取数据会被阻塞。因为此时还没有数据可取，直到队列中有了数据才能返回；如果队列已经满了，那么插入数据

的操作就会被阻塞，直到队列中有空闲位置后再插入数据，然后再返回。即 “生产者 - 消费者模型”，可使用阻塞队列实现一个“生产者 - 消费者模型”，这种基于阻塞队列实现的“生产者 - 消费者模型”，可以有效

地协调生产和消费的速度。当“生产者”生产数据的速度过快，“消费者”来不及消费时，存储数据的队列很快就会满了。这个时候，生产者就阻塞等待，直到“消费者”消费了数据，“生产者”才会被唤醒继续“生产”。

而且不仅如此，基于阻塞队列，我们还可以通过协调“生产者”和“消费者”的个数，来提高数据的处理效率。比如前面的例子，我们可以多配置几个“消费者”，来应对一个“生产者”。

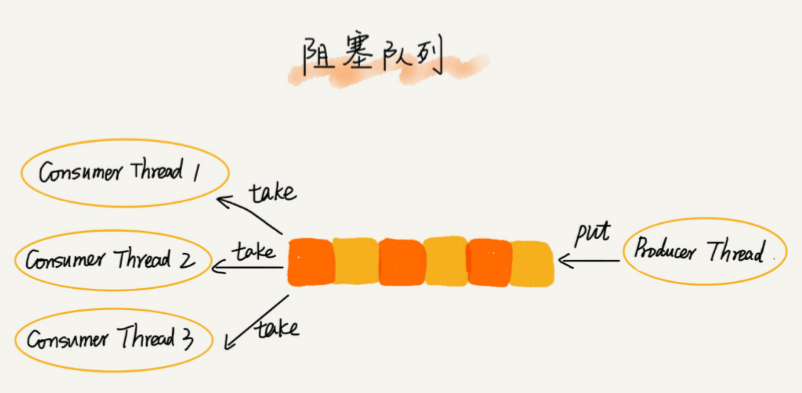
阻塞队列，在多线程情况下，会有多个线程同时操作队列，这个时候就会存在线程安全问题，如何实现一个线程安全的队列呢？

线程安全的队列我们叫作并发队列。最简单直接的实现方式是直接在 enqueue()、dequeue() 方法上加锁，但是锁粒度大并发度会比较低，同一时刻仅允许一个存或者取操作。实际上，基于数组的循环队列，利用 CAS 原子操作，可以实现非常高效的并发队列。这也是循环队列比链式队列应用更加广泛的原因。

2.5 优先队列 PriorityQueue

正常⼊、按照优先级出

实现了一个优先队列：从队首获取元素时，总是获取优先级最高的元素。

PriorityQueue默认按元素比较的顺序排序（必须实现Comparable接口），也可以通过Comparator自定义排序算法（元素就不必实现Comparable接口）。

PriorityQueue和Queue的区别在于，它的出队顺序与元素的优先级有关，对PriorityQueue调用remove()或poll()方法，返回的总是优先级最高的元素。

要使用PriorityQueue，我们就必须给每个元素定义“优先级”。

PriorityQueue -- 优先队列
    .正常入，按照优先级出；
优先队列已在很多语言中纳入标准库 
实现机制: 
① Heap(Binary, Binomial, Fibonacci)
② Binary Search Tree

2.6 双端队列 Deque （Double Ended Queue）

既可以添加到队尾，也可以添加到队首；
既可以从队首获取，又可以从队尾获取。

　　同时具有queue和stack的功能。

Deques can also be used as LIFO (Last-In-First-Out) stacks.  This
 * interface should be used in preference to the legacy {@link Stack} class.
 * When a deque is used as a stack, elements are pushed and popped from the
 * beginning of the deque.

Deque是一个接口，它的实现类有ArrayDeque和LinkedList （LinkedList真是一个全能选手，它即是List，又是Queue，还是Deque）

// 不推荐的写法: LinkedList<String> deque = new LinkedList<>();
// 推荐的写法：  Deque<String> deque = new LinkedList<>(); （面向抽象编程的一个原则就是：尽量持有接口，而不是具体的实现类。）

将元素添加到队首： addFirst()即push() /offerFirst()；　　
将元素添加到队尾：addLast()即add() /offerLast() 即offer() 　　
从队首获取元素并删除：removeFirst()即remove() pop() / pollFirst() 即poll() 　
从队尾获取元素并删除：removeLast()/pollLast()；
从队首获取元素但不删除：getFirst()/peekFirst() peek() 　　
从队尾获取元素但不删除：getLast()/peekLast()；
总是调用xxxFirst()/xxxLast()以便与Queue的方法区分开；
避免把null添加到队列。

如果直接写deque.offer()，我们就需要思考，offer()实际上是offerLast()，我们明确地写上offerLast()，不需要思考就能一眼看出这是添加到队尾。
因此，使用Deque，推荐总是明确调用offerLast() /offerFirst()或者pollFirst() /pollLast()方法。

2.7 队列的应用

1. 队列在线程池等有限资源池中的应用

CPU 资源是有限的，任务的处理速度与线程个数并不是线性正相关。相反，过多的线程反而会导致 CPU 频繁切换，处理性能下降。所以，线程池的大小一般都是综合考虑要处理任务的特点和硬件环境，来事先设置的。

当我们向固定大小的线程池中请求一个线程时，如果线程池中没有空闲资源了，这个时候线程池如何处理这个请求？是拒绝请求还是排队请求？各种处理策略又是怎么实现的呢？

两种处理策略：

一种是非阻塞的处理方式，直接拒绝任务请求；
一种是阻塞的处理方式，将请求排队，等到有空闲线程时，取出排队的请求继续处理。

那如何存储排队的请求呢？

公平地处理每个排队的请求，先进者先服务，所以队列这种数据结构很适合来存储排队请求。队列有基于链表和基于数组这两种实现方式。这两种实现方式对于排队请求又有什么区别呢？

　　基于链表的实现方式，可以实现一个支持无限排队的无界队列（unbounded queue），但是可能会导致过多的请求排队等待，请求处理的响应时间过长。所以，针对响应时间比较敏感的系统，基于链表实现的无限排队的线程池是不合适的。

　　基于数组实现的有界队列（bounded queue），队列的大小有限，所以线程池中排队的请求超过队列大小时，接下来的请求就会被拒绝，这种方式对响应时间敏感的系统来说，就相对更加合理。不过，设置一个合理的队列大小，也是非常有讲究的。队列太大导致等待的请求太多，队列太小会导致无法充分利用系统资源、发挥最大性能。

2. 队列应用在线程池请求排队的场景之外，队列可以应用在任何有限资源池中，用于排队请求，比如数据库连接池等。实际上，对于大部分资源有限的场景，当没有空闲资源时，基本上都可以通过“队列”这种数

据结构来实现请求排队。

3. 分布式消息队列，如 kafka 也是一种队列。

4. 并发队列，关于如何实现无锁并发队列。考虑使用CAS实现无锁队列，则在入队前，获取tail位置，入队时比较tail是否发生变化，如果否，则允许入队，反之，本次入队失败。出队则是获取head位置，进行cas。 CAS+数组。

posted @ 2020-06-14 16:28 kris12 阅读(343) 评论(0) 编辑收藏举报

刷新页面返回顶部

kris12

Self-discipline gives me freedom.

数据结构-04 |栈 |队列

概述

1. Java中栈的实现API

2. Java中Queue队列的API

3. 双端队列Deque的API

4. 优先队列PriorityQueue的API

1. 栈Stack

1.1 概念与特性

1.2 如何实现一个“栈”？

1.3 支持动态扩容的顺序栈

1.3 栈的应用

2. 队列Queue

2.1 概念和特性

2.2 顺序队列和链式队列

2.3 循环队列

2.4 阻塞队列和并发队列

2.5 优先队列 PriorityQueue

2.6 双端队列 Deque （Double Ended Queue）

2.7 队列的应用

公告