推荐系统| 基于协同过滤
3. 基于协同过滤的推荐算法 （用户和物品的关联）
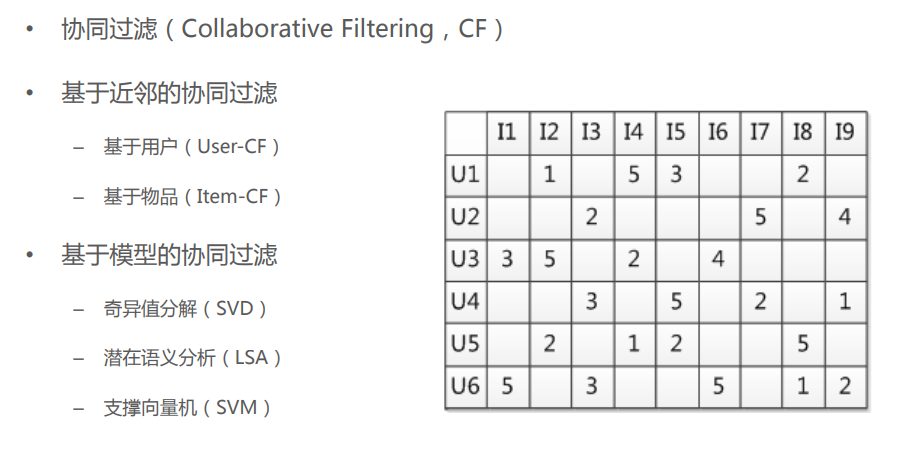
协同过滤（Collaborative Filtering，CF）-- 用户和物品之间关联的用户行为数据
- ①基于近邻的协同过滤
基于用户（User-CF） --用户画像
基于物品（Item-CF） -- 基于内容-特征工程
- ②基于模型的协同过滤
奇异值分解（SVD）
潜在语义分析（LSA）
支撑向量机（SVM）
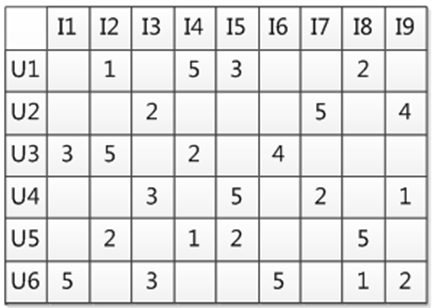
协同过滤CF -- 用户行为数据
- 基于内容（Content based，CB）（物品的信息拿不到基于内容就无法做了）主要利用的是用户评价过的物品的内容特征，而CF方法还可以利用其他用户评分过的物品内容
- CF 可以解决 CB 的一些局限 （用户评价可得出物品的好坏，但CF无法做出冷启动，基于大量数据）
物品内容不完全或者难以获得时，依然可以通过其他用户的反馈给出推荐
CF基于用户之间对物品的评价质量，避免了CB仅依赖内容可能造成的对物品质量判断的干扰
CF推荐不受内容限制，只要其他类似用户给出了对不同物品的兴趣，CF就可以给用户推荐出内容差异很大的物品（但有某种内在联系）
- 分为两类：基于近邻和基于模型
①. 基于近邻的推荐
基于近邻（基于用户之间的关联）的推荐系统根据的是相同“口碑”准则
是否应该给Cary推荐《泰坦尼克号》？
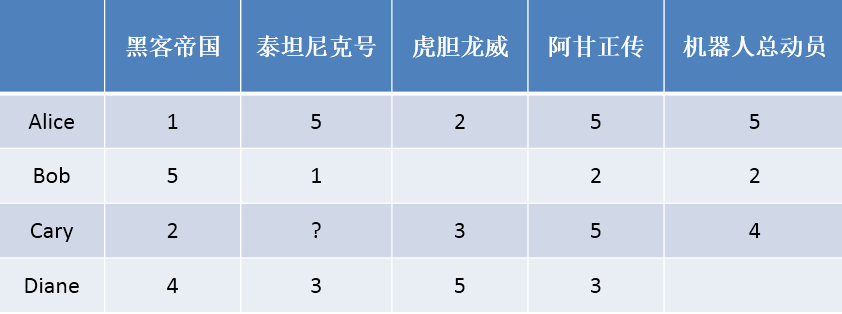
基于用户的协同过滤（User-CF） 用户的行为数据
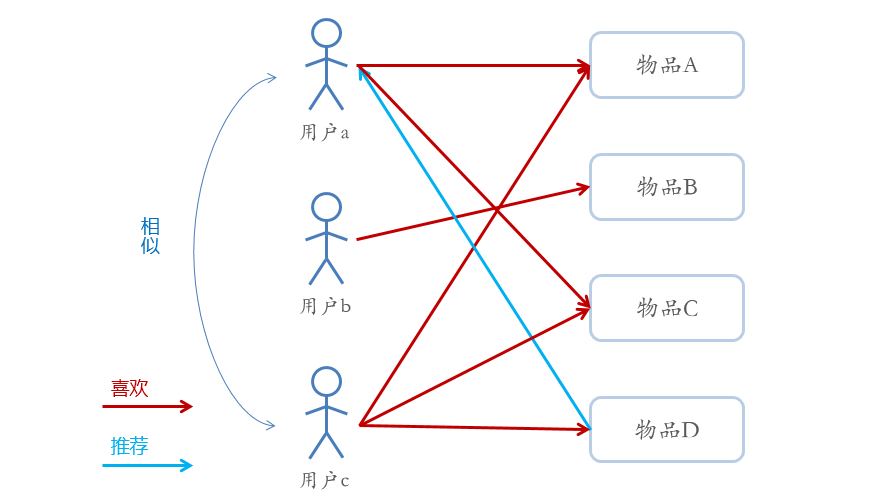
- 基于用户的协同过滤推荐的基本原理是，根据所有用户对物品的偏好，发现与当前用户口味和偏好相似的“邻居”用户群，并推荐近邻所偏好的物品
- 在一般的应用中是采用计算“K- 近邻”的算法；基于这 K 个邻居的历史偏好信息，为当前用户进行推荐
- User-CF 和基于人口统计学的推荐机制
两者都是计算用户的相似度，并基于相似的“邻居”用户群计算推荐
它们所不同的是如何计算用户的相似度：基于人口统计学的机制只考虑用户本身的特征，而基于用户的协同过滤机制可是在用户的历史偏好的数据上计算用户的相似度，它的基本假设是，喜欢类似物品的用户可能有相同或者相似的口味和偏好
基于物品的协同过滤（Item-CF）
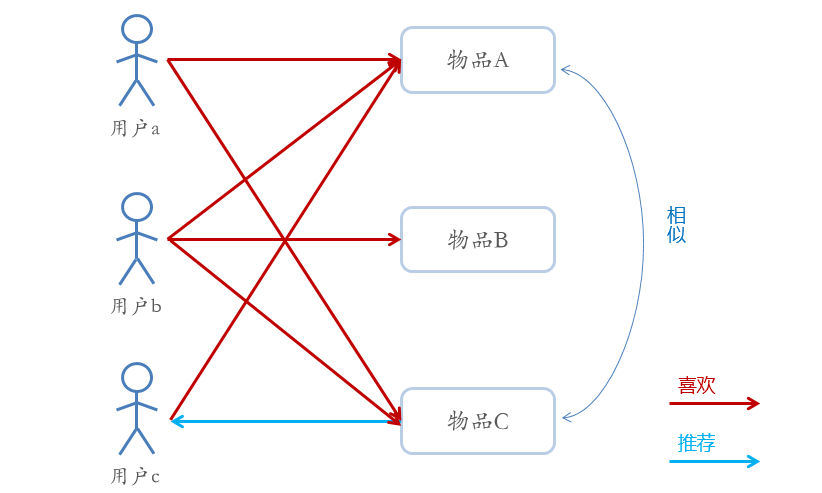
- 基于项目的协同过滤推荐的基本原理与基于用户的类似，只是使用所有用户对物品的偏好，发现物品和物品之间的相似度，然后根据用户的历史偏好信息，将类似的物品推荐给用户
- Item-CF 和基于内容（CB）的推荐
其实都是基于物品相似度预测推荐，只是相似度计算的方法不一样，前者是从用户历史的偏好推断，而后者是基于物品本身的属性特征信息
- 同样是协同过滤，在基于用户和基于项目两个策略中应该如何选择呢？
电商、电影、音乐网站，用户数量远大于物品数量
新闻网站，物品（新闻文本）数量可能大于用户数量
User-CF 和 Item-CF 的比较
同样是协同过滤，在 User-CF 和 Item-CF 两个策略中应该如何选择呢？
Item-CF 应用场景 -- 用户行为数据 -- 主流
基于物品的协同过滤（Item-CF）推荐机制是 Amazon 在基于用户的机制上改良的一种策略。因为在大部分的 Web 站点中，物品的个数是远远小于用户的数量的，而且物品的个数和相似度相对比较稳定，同时基于物品的机制比基于用户的实时性更好一些，所以 Item-CF 成为了目前推荐策略的主流
User-CF 应用场景
设想一下在一些新闻推荐系统中，也许物品——也就是新闻的个数可能大于用户的个数，而且新闻的更新程度也有很快，所以它的相似度依然不稳定，这时用 User-CF可能效果更好；
所以，推荐策略的选择其实和具体的应用场景有很大的关系
基于协同过滤的推荐优缺点
优点：
它不需要对物品或者用户进行严格的建模，而且不要求对物品特征的描述是机器可理解的，所以这种方法也是领域无关的
这种方法计算出来的推荐是开放的，可以共用他人的经验，很好的支持用户发现潜在的兴趣偏好
存在的问题：
方法的核心是基于历史数据，所以对新物品和新用户都有“冷启动”的问题
推荐的效果依赖于用户历史偏好数据的多少和准确性
在大部分的实现中，用户历史偏好是用稀疏矩阵进行存储的，而稀疏矩阵上的计算有些明显的问题，包括可能少部分人的错误偏好会对推荐的准确度有很大的影响等等
对于一些特殊品味的用户不能给予很好的推荐
②基于模型的协同过滤思想
基本思想
用户具有一定的特征，决定着他的偏好选择；
物品具有一定的特征，影响着用户需是否选择它；
用户之所以选择某一个商品，是因为用户特征与物品特征相互匹配；
基于这种思想，模型的建立相当于从行为数据中提取特征，给用户和物品同时打上“标签”；这和基于人口统计学的用户标签、基于内容方法的物品标签本质是一样的，都是特征的提取和匹配；
有显性特征时（比如用户标签、物品分类标签）我们可以直接匹配做出推荐；没有时，可以根据已有的偏好数据，去发掘出隐藏的特征，这需要用到隐语义模型（LFM）
基于模型的协同过滤推荐，就是基于样本的用户偏好信息，训练一个推荐模型，然后根据实时的用户喜好的信息进行预测新物品的得分，计算推荐
基于近邻的推荐和基于模型的推荐 -- 用的都是用户行为数据
基于近邻的推荐是在预测时直接使用已有的用户偏好数据，通过近邻数据来预测对新物品的偏好（类似分类）
而基于模型的方法，是要使用这些偏好数据来训练模型，找到内在规律，再用模型来做预测（类似回归）
训练模型时，可以基于标签内容来提取物品特征，也可以让模型去发掘物品的潜在特征；这样的模型被称为 隐语义模型（Latent Factor Model，LFM）
隐语义模型（LFM）
用隐语义模型来进行协同过滤的目标
揭示隐藏的特征，这些特征能够解释为什么给出对应的预测评分
这类特征可能是无法直接用语言解释描述的，事实上我们并不需要知道，类似“玄学”
通过矩阵分解进行降维分析
协同过滤算法非常依赖历史数据，而一般的推荐系统中，偏好数据又往往是稀疏的；这就需要对原始数据做降维处理
分解之后的矩阵，就代表了用户和物品的隐藏特征
隐语义模型的实例：
基于概率的隐语义分析（pLSA）
隐式迪利克雷分布模型（LDA）
矩阵因子分解模型（基于奇异值分解的模型，SVD）
LFM 降维方法 —— 矩阵因子分解
假设用户物品评分矩阵为 R，现在有 m 个用户，n 个物品
我们想要发现 k 个隐类（用户和物品的隐藏特征），我们的任务就是找到两个矩阵 P 和 Q，使这两个矩阵的乘积近似等于 R，即将用户物品评分矩阵 R 分解成为两个低维矩阵相乘：
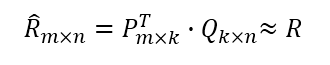用户的在m行中K个隐藏特征，
矩阵因子分解
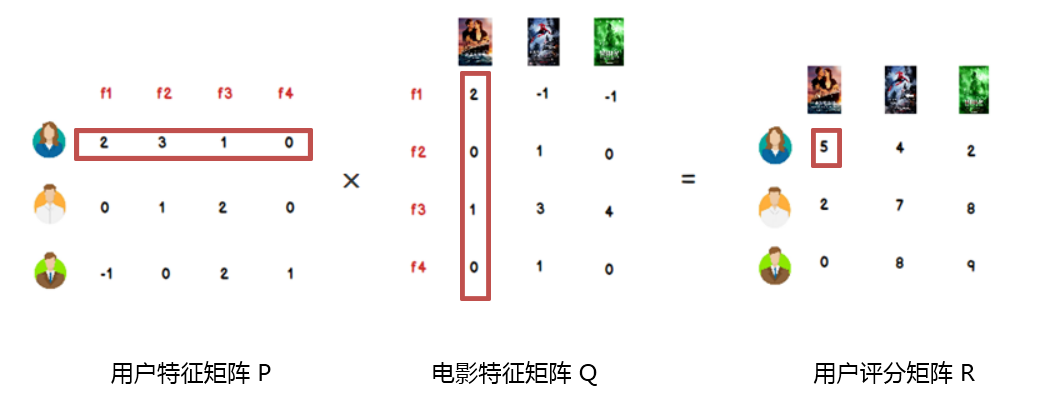
LFM 的进一步理解
我们可以认为，用户之所以给电影打出这样的分数，是有内在原因的，我们可以挖掘出影响用户打分的隐藏因素，进而根据未评分电影与这些隐藏因素的关联度，决定此未评分电影的预测评分；
应该有一些隐藏的因素，影响用户的打分，比如电影：演员、题材、年代…甚至不一定是人直接可以理解的隐藏因子；
找到隐藏因子，可以对 user 和 item 进行关联（找到是由于什么使得 user 喜欢/不喜欢此 item，什么会决定 user 喜欢/不喜欢此 item），就可以推测用户是否会喜欢某一部未看过的电影。
对于用户看过的电影，会有相应的打分，但一个用户不可能看过所有电影，对于用户没有看过的电影是没有评分的，因此用户评分矩阵大部分项都是空的，是一个稀疏矩阵
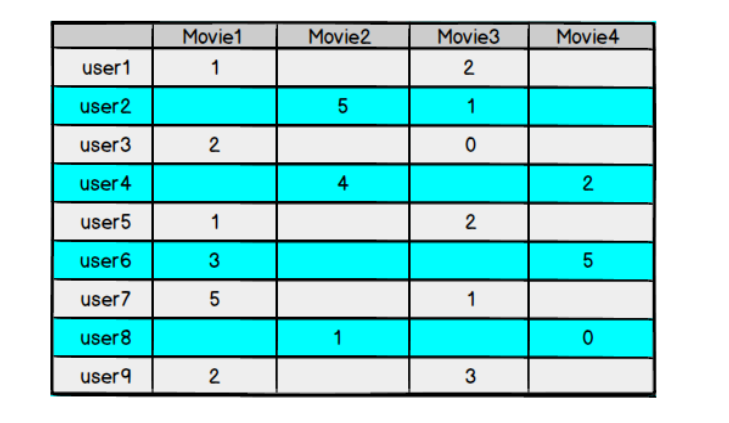
如果我们能够根据用户给已有电影的打分推测出用户会给没有看过的电影的打分，那么就可以根据预测结果给用户推荐他可能打高分的电影
矩阵因子分解
我们现在来做一个一般性的分析
一个 m×n 的打分矩阵 R 可以用两个小矩阵 Pm×k 和 Qk×n 的乘积 𝑅 ̂ 来近似：
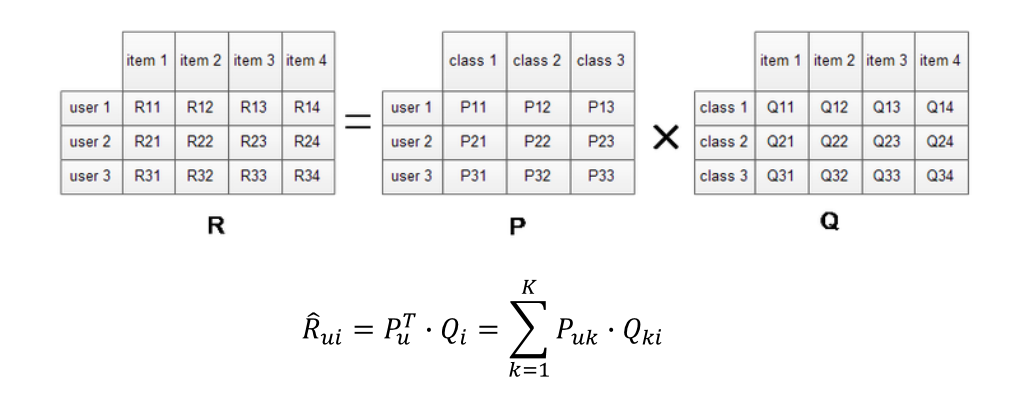
得到 Pm×k 和 Qk×n 的乘积 𝑅 ̂ 不再是稀疏的，之前 R 中没有的项也可以由 P、Q 的乘积算出，这就得到了一个 预测评分矩阵；
P定义的是一列，构成的用户特征，某一个用户的特征；Qi表示某个物品的特征向量；Rui表某一个用户对物品的评分
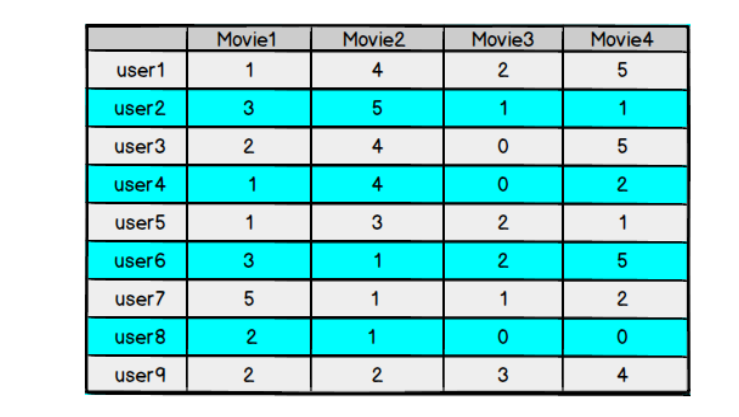
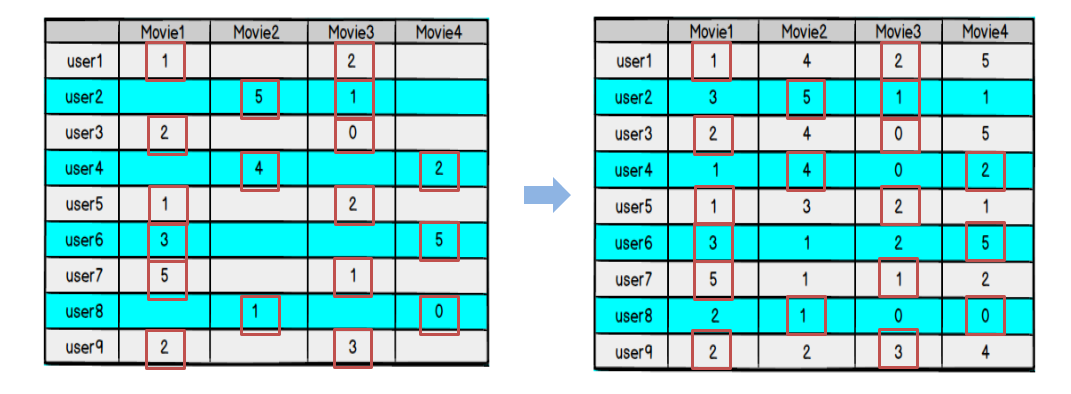
如果得到的预测评分矩阵 𝑅 ̂ 与原评分矩阵 R 在已知评分位置上的值都近似，那么我们认为它们在预测位置上的值也是近似的
模型的求解 —— 损失函数
现在的问题是，怎样得到这样的分解方式 𝑅 ̂=𝑃×𝑄 呢？
矩阵分解得到的预测评分矩阵 𝑅 ̂，与原评分矩阵 R 在已知的评分项上可能会有误差，我们的目标是找到一个最好的分解方式，让分解之后的预测评分矩阵总误差最小
损失函数
我们选择平方损失函数，并且加入正则化项，以防过拟合
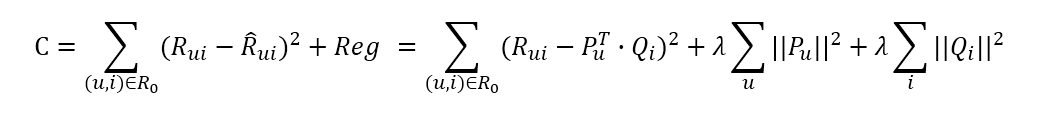
模型的求解算法 —— ALS
现在，矩阵因子分解的问题已经转化成了一个标准的优化问题，需要求解 P、Q，使目标损失函数取最小值
最小化过程的求解，一般采用随机梯度下降算法或者交替最小二乘法来实现
交替最小二乘法（Alternating Least Squares，ALS）：
ALS的思想是，由于两个矩阵P和Q都未知，且通过矩阵乘法耦合在一起，为了使它们解耦，可以先固定Q，把P当作变量，通过损失函数最小化求出P，这就是一个经典的最小二乘问题；再反过来固定求得的P，把Q当作变量，求解出Q：如此交替执行，直到误差满足阈值条件，或者到达迭代上限。
ALS算法具体过程如下：
① 为 Q 指定一个初值 Q0，可以是 随机生成或者全局平均值
②固定当前 Q0 值，求解 P0
③固定当前 P0 值，求解 Q1
④固定当前 Q1 值，求解 P1
⑤…（重复以上过程）
⑥直到损失函数的值 C 收敛，迭代结束
求解过程
以固定 Q，求解 P为例
由于每一个用户 u 都是相互独立的，当 Q 固定时，用户特征向量 Pu 应该取得的值与其它用户特征向量无关；所以每一个 Pu 都可以单独求解
优化目标 min┬(𝑃,𝑄)𝐶 可转化为
ALS 算法
梯度下降算法
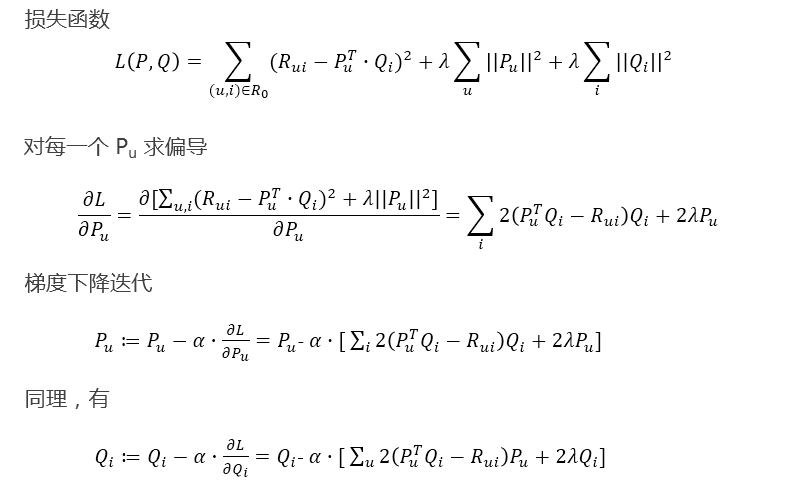
LFM梯度下降算法实现
import numpy as np import pandas as pd 1. 数据准备 # 评分矩阵R R = np.array([[4,0,2,0,1], [0,2,3,0,0], [1,0,2,4,0], [5,0,0,3,1], [0,0,1,5,1], [0,3,2,4,1],]) len(R[0]) ====> 5 2. 算法实现 """ @输入参数： R：M*N 的评分矩阵 K：隐特征向量维度 max_iter: 最大迭代次数 alpha：步长 lamda：正则化系数 @输出： 分解之后的 P，Q P：初始化用户特征矩阵M*K Q：初始化物品特征矩阵N*K """ # 给定超参数 K = 5 max_iter = 5000 alpha = 0.0002 lamda = 0.004 # 核心算法 def LFM_grad_desc( R, K=2, max_iter=1000, alpha=0.0001, lamda=0.002 ): # 基本维度参数定义 M = len(R) N = len(R[0]) # P,Q初始值，随机生成 P = np.random.rand(M, K) Q = np.random.rand(N, K) Q = Q.T # 开始迭代 for step in range(max_iter): # 对所有的用户u、物品i做遍历，对应的特征向量Pu、Qi梯度下降 for u in range(M): for i in range(N): # 对于每一个大于0的评分，求出预测评分误差 if R[u][i] > 0: eui = np.dot( P[u,:], Q[:,i] ) - R[u][i] # 代入公式，按照梯度下降算法更新当前的Pu、Qi for k in range(K): P[u][k] = P[u][k] - alpha * ( 2 * eui * Q[k][i] + 2 * lamda * P[u][k] ) Q[k][i] = Q[k][i] - alpha * ( 2 * eui * P[u][k] + 2 * lamda * Q[k][i] ) # u、i遍历完成，所有特征向量更新完成，可以得到P、Q，可以计算预测评分矩阵 predR = np.dot( P, Q ) # 计算当前损失函数 cost = 0 for u in range(M): for i in range(N): if R[u][i] > 0: cost += ( np.dot( P[u,:], Q[:,i] ) - R[u][i] ) ** 2 # 加上正则化项 for k in range(K): cost += lamda * ( P[u][k] ** 2 + Q[k][i] ** 2 ) if cost < 0.0001: break return P, Q.T, cost 3. 测试 P, Q, cost = LFM_grad_desc(R, K, max_iter, alpha, lamda) print(P) print(Q) print(cost) predR = P.dot(Q.T) print(R) predR
