算法-06 | 排序
1. 概述
https://www.cnblogs.com/onepixel/p/7674659.html
https://www.bilibili.com/video/av25136272
https://www.bilibili.com/video/av63851336
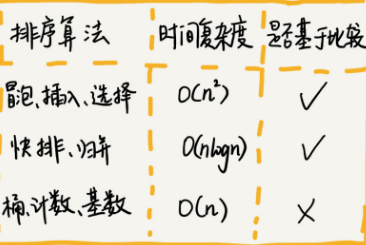
1.1 比较类排序
通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此也称为非线性时间比较类排序。
包含初级排序O(n2) 冒泡、插入、选择，高级排序O(nLlogn)快排、归并；
高级语言中直接调系统自带的排序函数，可以传进去一个comparator，可以比较任何结构体或对象
1.2 非比较类排序
不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。
包含O(n)桶、计数、基数排序等。
它的缺点是一般只能用于整型相关的数据类型，比如对于字符串或对象之间的排序就无能为力了。同时它一般要辅助用额外的内存空间。
1.3 各类排序算法复杂度的分析
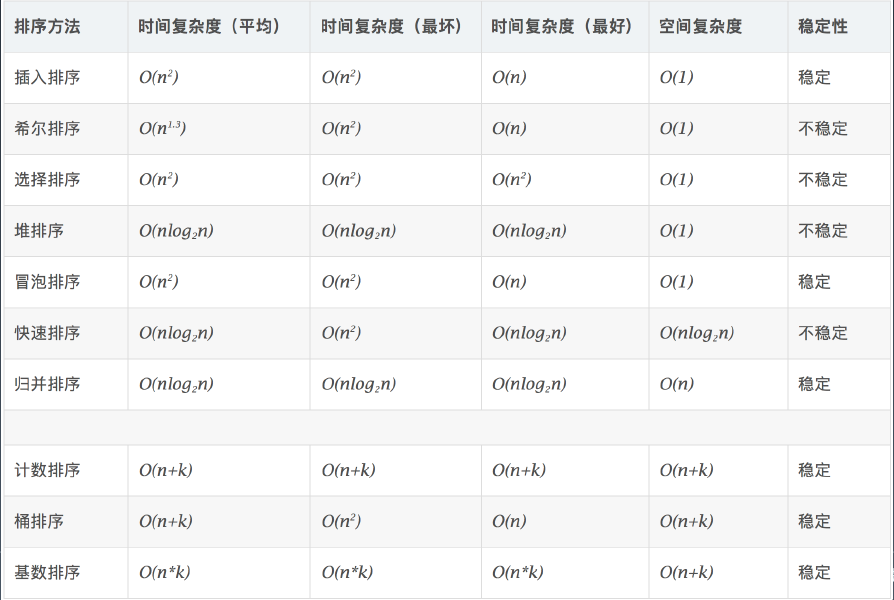
优先级：nlogn的排序，即堆排序、快速排序、归并排序。
1.4 如何分析一个排序算法
排序算法的执行效率
① 最好情况、最坏情况、平均情况时间复杂度（它们所对应要排序的原始数据是怎样的）；
② 时间复杂度的系数、常数 、低阶（实际开发中排序规模较小，而时间复杂度反应的是数据规模 n 很大时候一个增长趋势会忽略系数、常数、低价，这时要把它们考虑进来）；
③ 比较次数和交换（或移动）次数（基于比较的排序算法的执行过程，涉及的两种操作，一是元素比较大小，另一种是元素交换或移动）；
平均时间复杂度就是加权平均期望时间复杂度，分析的时候要结合概率论的知识。还有一种思路，通过“有序度”和“逆序度”这两个概念来进行分析。
有序度是数组中具有有序关系的元素对的个数。有序元素对用数学表达式表示就是这样：有序元素对：a[i] <= a[j], 如果 i < j。
对于一个倒序排列（从大到小）的数组，比如 6，5，4，3，2，1，有序度是 0，逆序度即 n *（n-1）/ 2；
对于一个完全有序（从小到大）的数组，比如 1，2，3，4，5，6，有序度就是 n *（n-1）/ 2，也就是 15， 这种完全有序的数组的有序度叫作满有序度。
逆序度定义正好跟有序度相反（默认从小到大为有序），逆序元素对：a[i] > a[j], 如果 i < j。
逆序度 = 满有序度 - 有序度。我们排序的过程就是一种增加有序度，减少逆序度的过程，最后达到满有序度，就说明排序完成了。
排序算法的内存消耗
算法的内存消耗可以通过空间复杂度来衡量，针对排序算法的空间复杂度，还引入一个新的概念，原地排序（Sorted in place）算法，特指空间复杂度是 O(1) 的排序算法。
排序算法的稳定性
仅仅用执行效率和内存消耗来衡量排序算法的好坏是不够的。针对排序算法，还有一个重要的度量指标，稳定性。即如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变。
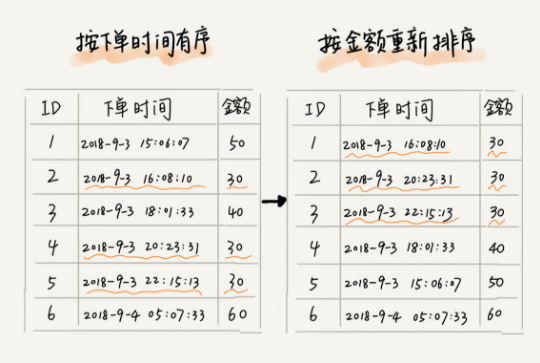
例如：现有 10 万条订单数据，希望按照金额从小到大对订单数据排序，对于金额相同的订单，按照下单时间从早到晚有序。
最先想到的方法是：先按照金额对订单数据进行排序，然后，再遍历排序之后的订单数据，对于每个金额相同的小区间再按下单时间排序。这种实现起来会很复杂。
借助稳定排序算法，这个问题可以非常简洁地解决。解决思路：先按下单时间给订单排序，不是金额。排序完成之后用稳定排序算法，按照订单金额重新排序。两遍排序之后，得到的订单数据就是按金额从小到大排序，金额相同的订单按下单时间从早到晚排序。
稳定排序算法可以保持金额相同的两个对象，在排序之后的前后顺序不变。
2. 初级排序 - O(n^2)
冒泡排序和插入排序的时间复杂度都是 O(n2)，都是原地排序算法，但插入排序比冒泡排序更受欢迎。
冒泡排序不管怎么优化，元素交换的次数是一个固定值，是原始数据的逆序度。插入排序是同样的，不管怎么优化，元素移动的次数也等于原始数据的逆序度。
但是，从代码实现上来看，冒泡排序的数据交换要比插入排序的数据移动要复杂，冒泡排序需要 3 个赋值操作，而插入排序只需要 1 个。
//冒泡排序中数据的交换操作：
if(a[j]>a[j+1]) { // 交换
int tmp = a[j];
a[j] = a[j + 1];
a[j + 1] = tmp;
flag = true;
}
//插入排序中数据的移动操作：
if(a[j]>value) {
a[j + 1] = a[j]; // 数据移动
} else {
break;
}
用冒泡排序，每次需要 3 个赋值语句，所以交换操作总耗时就是 3*K 单位时间。而插入排序中数据移动操作只需要 K 个单位时间。
虽然冒泡排序和插入排序在时间复杂度上是一样的，都是 O(n2)，但是如果我们希望把性能优化做到极致，那肯定首选插入排序。插入排序的算法思路也有很大的优化空间
2.1 冒泡排序（Bubble Sort）
冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置，重复 n 次，就完成了 n 个数据的排序工作。
嵌套循环，每次查看相邻的元素如果逆序，则交换。
// 冒泡排序，a 表示数组，n 表示数组大小
public void bubbleSort(int[] a, int n) {
if (n <= 1) return;
for (int i = 0; i < n; ++i) {
// 提前退出冒泡循环的标志位
boolean flag = false;
for (int j = 0; j < n - i - 1; ++j) {
if (a[j] > a[j+1]) { // 交换
int tmp = a[j];
a[j] = a[j+1];
a[j+1] = tmp;
flag = true; // 表示有数据交换
}
}
if (!flag) break; // 没有数据交换，提前退出
}
}
冒泡的过程只涉及相邻数据的交换操作，只需要常量级的临时空间，所以它的空间复杂度为 O(1)，是一个原地排序算法。
在冒泡排序中，只有交换才可以改变两个元素的前后顺序。为了保证冒泡排序算法的稳定性，当有相邻的两个元素大小相等的时候，不做交换，相同大小的数据在排序前后不会改变顺序，所以冒泡排序是稳定的排序算法；
最好情况下，要排序的数据已经是有序的了，我们只需要进行一次冒泡操作，就可以结束了，所以最好情况时间复杂度是 O(n)。而最坏的情况是，要排序的数据刚好是倒序排列的，我们需要进行 n 次冒泡操作，所以最坏情况时间复杂度为 O(n2)。
对于包含 n 个数据的数组进行冒泡排序，平均交换次数是多少呢？最坏情况下，初始状态的有序度是 0，所以要进行 n*(n-1)/2 次交换。最好情况下，初始状态的有序度是 n*(n-1)/2，就不需要进行交换。取个中间值 n*(n-1)/4，来表示初始有序度既不是很高也不是很低的平均情况。
即平均情况下，需要 n*(n-1)/4 次交换操作，比较操作肯定要比交换操作多，而复杂度的上限是 O(n2)，所以平均情况下的时间复杂度就是 O(n2)。
这个平均时间复杂度推导过程其实并不严格，但是很多时候很实用。
2.2 插入排序（Insertion Sort）
从前到后逐步构建有序序列；对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。
public static void insertionSort(int[] nums, int n) {
if (n <= 1) return;
for (int i = 1; i < n; i++) {
int value = nums[i];
int j = i - 1;
//查找插入位置, 如果前边的数 < value, 说明是有序的继续遍历下一个value
for (; j >= 0; j--) {
if (nums[j] > value) {
nums[j + 1] = nums[j];//数据移动, 第j + 1 和 j 位赋相同的值, 最后再还原为value 值
} else
break;// num[j] < value, 结束循环
}
nums[j + 1] = value;//插入数据, 还原为value 值
}
}
}
插入排序算法的运行并不需要额外的存储空间，所以空间复杂度是 O(1)，也就是说，这是一个原地排序算法。
在插入排序中，对于值相同的元素，我们可以选择将后面出现的元素，插入到前面出现元素的后面，这样就可以保持原有的前后顺序不变，所以插入排序是稳定的排序算法。
如果排序的数据是有序的，并不需搬移任何数据，从尾到头在有序数据组里面查找插入位置，每次只需要比较一个数据就能确定插入的位置。最好是时间复杂度为 O(n)。
如果数组是倒序的，每次插入都相当于在数组的第一个位置插入新的数据，所以需要移动大量的数据，最坏情况时间复杂度为 O(n2)。
在数组中插入一个数据的平均时间复杂度是 O(n)。所以，对于插入排序来说，每次插入操作都相当于在数组中插入一个数据，循环执行 n 次插入操作，所以平均时间复杂度为 O(n2)。
2.3 选择排序（Selection Sort）
每次找最小值，然后放到待排序数组的起始位置。
public static void selectionSort(int[] nums, int n) {
if (n <= 1) return;
for (int i = 0; i < n - 1; i++) {
//查找最小值 的下标 index
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (nums[j] < nums[minIndex]) {
minIndex = j;
}
}
//交换
int tmp = nums[i];
nums[i] = nums[minIndex];
nums[minIndex] = tmp;
}
}
选择排序空间复杂度为 O(1)，是一种原地排序算法。选择排序的最好情况时间复杂度、最坏情况和平均情况时间复杂度都为 O(n2)。
选择排序是一种不稳定的排序算法。选择排序每次都要找剩余未排序元素中的最小值，并和前面的元素交换位置，这样破坏了稳定性。
5，8，5，2，9 这样一组数据，使用选择排序算法来排序的话，第一次找到最小元素 2，与第一个 5 交换位置，那第一个 5 和中间的 5 顺序就变了，所以就不稳定了。正是因此，相对于冒泡排序和插入排序，选择排序就稍微逊色了。
特定算法是依赖特定的数据结构的。上边这几种排序算法，都是基于数组实现的。如果数据存储在链表中，这三种排序算法还能工作吗？如果能，那相应的时间、空间复杂度又是多少呢？
前提条件是是否允许修改链表的节点value值，还是只能改变节点的位置。
一般而言，考虑只能改变节点位置，冒泡排序相比于数组实现，比较次数一致，但交换时操作更复杂；
插入排序，比较次数一致，不需要再有后移操作，找到位置后可以直接插入，但排序完毕后可能需要倒置链表；
选择排序比较次数一致，交换操作同样比较麻烦。
综上，时间复杂度和空间复杂度并无明显变化，若追求极致性能，冒泡排序的时间复杂度系数会变大，插入排序系数会减小，选择排序无明显变化。
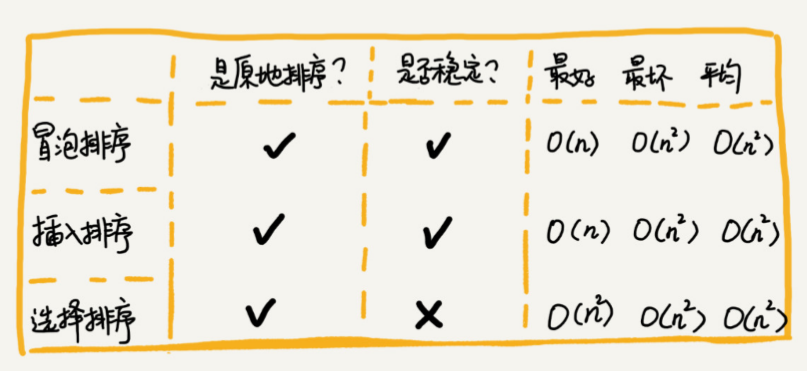
冒泡、插入、选择排序都有一个共同点，将待排序数列分为已排序和未排序两部分。在未排序的部分中查找一个最值，放到已排序数列的恰当位置。
具体到代码层面，外层循环的变量用于分割已排序和未排序数，内层循环的变量用于在未排序数中查找。
3. 高级排序 - O(nLogn)
冒泡排序、插入排序、选择排序这三种排序算法，它们的时间复杂度都是 O(n2)，比较高，适合小规模数据的排序；
归并排序和快速排序，这两种排序算法适合大规模的数据排序，时间复杂度为 O(nlogn) ，都用到了分治思想。
3.1 归并排序（Merge Sort）— 分治
1. 把长度为n的输入序列分成两个长度为n/2的子序列；
2. 对这两个子序列分别采用归并排序；
3. 将两个排序好的子序列合并成一个最终的排序序列。
public static void mergeSort(int[] array, int left, int right) {
//1. 递归终止条件
if (left >= right) return;
int mid = (left + right) >> 1;
//2. 分治递归
mergeSort(array, left, mid);
mergeSort(array, mid + 1, right);
//3. 将array[left, mid]和 array[mid + 1, right] 合并为 array[left, right]
merge(array, left, mid, right);
}
private static void merge(int[] array, int left, int mid, int right) {
//临时缓存 数组
int[] temp = new int[right - left + 1];
//mid中间下标, i -> mid 往左遍历, mid -> right 往右遍历； i, j分别指向array[left, mid] 和 array[mid+1, right] 的第一个元素
int i = left, j = mid + 1, k = 0;
while (i <= mid && j <= right) {
temp[k++] = array[i] <= array[j] ? array[i++] : array[j++];
}
while (i <= mid)
temp[k++] = array[i++];
while (j <= right)
temp[k++] = array[j++];
//把临时数组temp中数组拷贝到原数组中。
for (int p = 0; p < temp.length; p++) {
array[left + p] = temp[p];
}
// 也可以⽤ System.arraycopy(a, start1, b, start2, length)
}
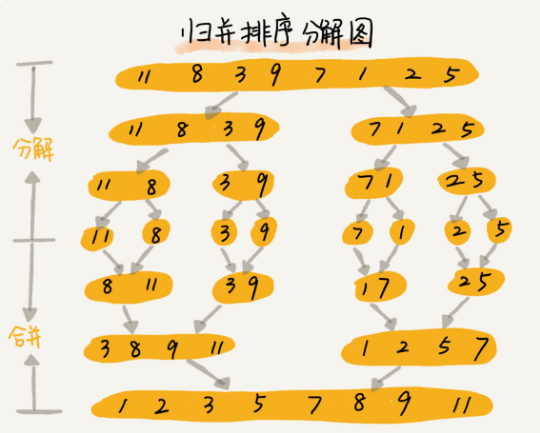
归并排序使用分治思想。分治，就是分而治之，将一个大问题分解成小的子问题来解决。小的子问题解决了，大问题也就解决了。
分治思想跟递归思想很像，分治算法一般都是用递归来实现的。分治是一种解决问题的处理思想，递归是一种编程技巧。
归并排序的递推公式：
递推公式：
mergeSort(left, right) = merge( mergeSort(left, mid), mergeSort(mid+1, right) )
终止条件：
left >= right 不用再继续分解
mergeSort( left, right ) 表示，给下标从 left 到 right 之间的数组排序。
将这个排序问题转化为两个子问题： mergeSort( left, mid) 和 mergeSort( mid + 1, right )，其中下标 mid 等于 left 和 right 的中间位置，也就是 ( left + right ) / 2。
当下标从 left 到 mid 和从 mid + 1 到 right 这两个子数组都排好序之后，我们再将两个有序的子数组合并在一起，这样下标从 left 到 right 之间的数据就也排好序了。
归并排序稳不稳定关键要看 merge() 函数，也就是两个有序子数组合并成一个有序数组的那部分代码。
在合并的过程中，如果 array[ left, mid ] 和 array[ mid + 1, right ] 之间有值相同的元素，可先把 array[ left, mid ] 中的元素放入 tmp 数组。这样就保证了值相同的元素，在合并前后的先后顺序不变。所以，归并排序是一个稳定的排序算法。
时间复杂度：
定义求解问题 a 的时间是 T(a)，求解问题 b、c 的时间分别是 T(b) 和 T( c)，得到一递推关系式：
T(a) = T(b) + T(c) + K, 其中 K 等于将两个子问题 b、c 的结果合并成问题 a 的结果所消耗的时间。
结论：不仅递归求解的问题可以写成递推公式，递归代码的时间复杂度也可以写成递推公式。
套用这个公式，分析归并排序的时间复杂度。
假设对 n 个元素进行归并排序需要的时间是 T(n)，那分解成两个子数组排序的时间都是 T(n/2)。我们知道，merge() 函数合并两个有序子数组的时间复杂度是 O(n)。
1)T(1) = C； n=1 时，只需要常量级的执行时间，所以表示为 C。
2)T(n) = 2*T(n/2) + n； n>1
T(n) = 2*T(n/2) + n
= 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
= 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
= 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n
......
= 2k * T(n/2k) + k * n
一步一步分解推导，我们可以得到 T(n) = 2k T(n/2k)+kn。当 T(n/2k)=T(1) 时，也就是 n/2k=1，我们得到 k=log2n 。我们将 k 值代入上面的公式，得到 T(n)=Cn+nlog2n 。
用大 O 标记法来表示的话，T(n) 就等于 O(nlogn)。所以归并排序的时间复杂度是 O(nlogn)。
原理分析和伪代码可以看出，归并排序的执行效率与要排序的原始数组的有序程度无关，所以其时间复杂度是非常稳定的，不管是最好情况、最坏情况，还是平均情况，时间复杂度都是 O(nlogn)。
时间复杂度是非常稳定的，最好情况、最坏情况，平均情况，时间复杂度都是 O(nlogn)；
空间复杂度：
归并排序并没有像快排应用广泛，因为它有一个致命的“弱点”，即归并排序不是原地排序算法。因为归并排序的合并函数，在合并两个有序数组为一个有序数组时，需要借助额外的存储空间。 尽管每次合并操作都需要申请额外的内存空间，但在合并完成之后，临时开辟的内存空间就被释放掉了。在任意时刻，CPU 只会有一个函数在执行，也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小，所以空间复杂度是 O(n)。
3.2 快速排序（Quick Sort）
快排利用的也是分治思想，快排思想：
如果要排序数组中下标从 begin 到 right 之间的一组数据，我们选择 begin 到 right 之间的任意一个数据作为 pivot（分区点）。
我们遍历 begin 到 right 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。经过这一步骤之后，数组 begin 到 right 之间的数据就被分成了三个部分，
前面 begin 到 mid - 1 之间都是小于 pivot 的，中间是 pivot，后面的 mid + 1 到 right 之间是大于 pivot 的。，然后依次对右边和右边的子数组继续快排；以达到整个序列有序。
public static void quickSort(int[] array, int begin, int end) {
if (begin >= end) return;
int pivot = partition(array, begin, end); //返回 counter 个数 (中间值左边数组 或者 右边数组的个数)
quickSort(array, begin, pivot - 1); //递归左边的值
quickSort(array, pivot + 1, end); //递归右边的值
}
private static int partition(int[] array, int begin, int end) {
// pivot: 标杆位置, counter: ⼩于pivot的元素的个数, 从左往右即从小到大计数
int pivot = end, counter = begin;
//1. 把小于 array[pivot] 的元素依次放数组左边,
for (int i = begin; i < end; i++) {
if (array[i] < array[pivot]) {
int temp = array[counter];
array[counter] = array[i];
array[i] = temp;
counter++;
}
}
//2. 将 array[pivot] 的值中间, 左边 < array[pivot] < 右边
int temp = array[pivot];
array[pivot] = array[counter];
array[counter] = temp;
return counter;
}
快排是一种原地、不稳定的排序算法
时间复杂度分析：
T(1) = C； n=1 时，只需要常量级的执行时间，所以表示为 C。
T(n) = 2*T(n/2) + n； n>1
T(1) = C； n=1 时，只需要常量级的执行时间，所以表示为 C。
T(n) = T(n/10) + T(9*n/10) + n； n>1
分治和快排区别：
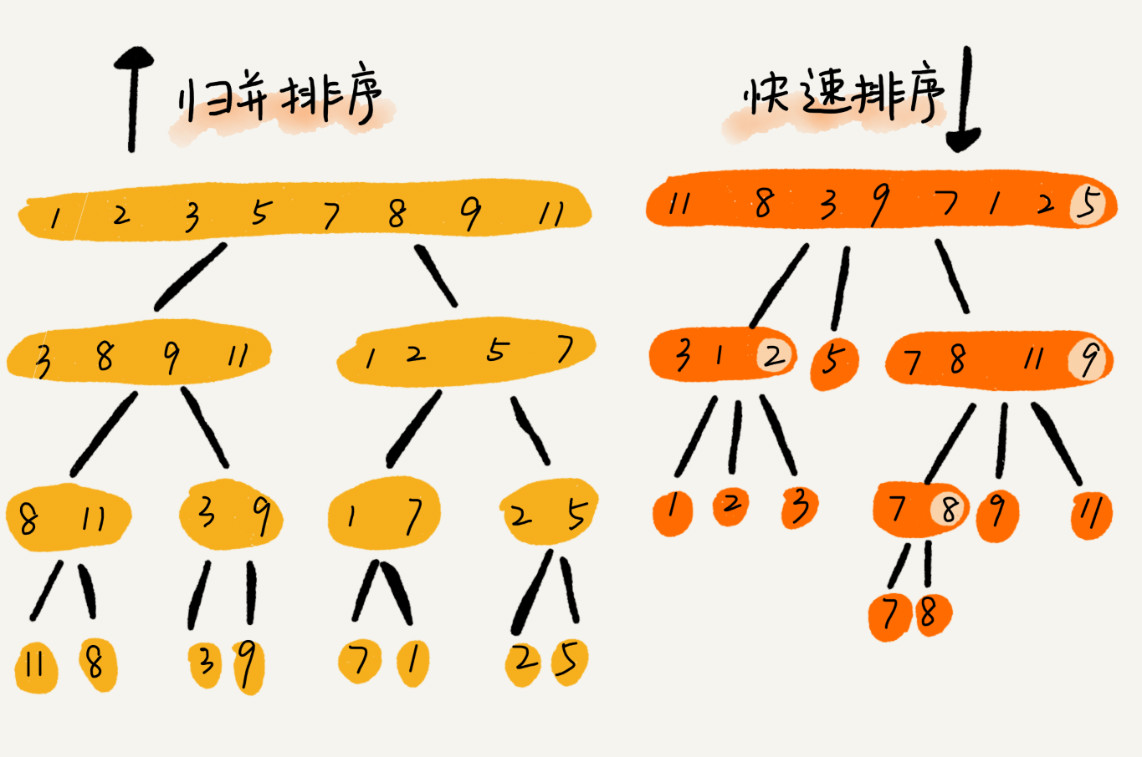
归并排序的处理过程是由下到上的，先处理子问题，然后再合并。而快排正好相反，它的处理过程是由上到下的，先分区，然后再处理子问题。
归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法，但是它是非原地排序算法。
归并之所以是非原地排序算法，主要原因是合并函数无法在原地执行。快速排序通过设计巧妙的原地分区函数，可以实现原地排序，解决了归并排序占用太多内存的问题。
归并：先排序左右子数组，然后合并两个有序子数组
快排：先调配出左右子数组，然后对于左右子数组进行排序
3.3 堆排序（Heap Sort） — 堆插入 O(logN)，取最大/小值 O(1)
1. 数组元素依次建立小顶堆
2. 依次取堆顶元素，并删除
https://www.cnblogs.com/shengyang17/p/13362354.html
C++：
void heap_sort(int a[], int len) { priority_queue<int, vector<int>, greater<int>> q; for (int i = 0; i < len; i++) { q.push(a[i]); } for (int i = 0; i < len; i++) { a[i] = q.pop(); } }
Java：
static void heapify(int[] array, int length, int i) {
int left = 2 * i + 1, right = 2 * i + 2;
int largest = i;
if (left < length && array[left] > array[largest]) {
largest = leftChild;
}
if (right < length && array[right] > array[largest]) {
largest = right;
}
if (largest != i) {
int temp = array[i];
array[i] = array[largest];
array[largest] = temp;
heapify(array, length, largest);
}
}
public static void heapSort(int[] array) {
if (array.length == 0) return;
int length = array.length;
for (int i = length / 2 - 1; i >= 0; i -)
heapify(array, length, i);
for (int i = length - 1; i >= 0; i--) {
int temp = array[0];
array[0] = array[i];
array[i] = temp;
heapify(array, i, 0);
}
}
4. 线性排序（Linear sort）- O(n)
桶排序、计数排序、基数排序，这些排序算法的时间复杂度是线性的，所以把这类排序算法叫作线性排序（Linear sort）。之所以能做到线性的时间复杂度，主要原因是，这三个算法是非基于比较的排序算法，都不涉及元素之间的比较操作。
但这三种排序对要排序的数据要求很苛刻。
4.1 桶排序（Bucket Sort）
桶排序 (Bucket sort)的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排）。
桶排序，核心思想是将要排序的数据分到几个有序的桶里，每个桶里的数据再单独进行排序。桶内排完序之后，再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。
桶排序的时间复杂度：
如果要排序的数据有 n 个，我们把它们均匀地划分到 m 个桶内，每个桶里就有 k = n / m 个元素。每个桶内部使用快速排序，时间复杂度为 O(k * logk)。
m 个桶排序的时间复杂度就是 O(m * k * logk)，因为 k = n / m，所以整个桶排序的时间复杂度就是 O(n*log( n/m))。当桶的个数 m 接近数据个数 n 时，log(n/m) 就是一个非常小的常量，这个时候桶排序的时间复杂度接近 O(n)。
桶排序对要排序数据的要求是非常苛刻的：
首先，要排序的数据需要很容易就能划分成 m 个桶，并且，桶与桶之间有着天然的大小顺序。这样每个桶内的数据都排序完之后，桶与桶之间的数据不需要再进行排序。
其次，数据在各个桶之间的分布是比较均匀的。如果数据经过桶的划分之后，有些桶里的数据非常多，有些非常少，很不平均，那桶内数据排序的时间复杂度就不是常量级了。在极端情况下，如果数据都被划分到一个桶里，那就退化为 O(nlogn) 的排序算法了。
桶排序比较适合用在外部排序中。所谓的外部排序就是数据存储在外部磁盘中，数据量比较大，内存有限，无法将数据全部加载到内存中。
比如说我们有 10GB 的订单数据，我们希望按订单金额（假设金额都是正整数）进行排序，但是我们的内存有限，只有几百 MB，没办法一次性把 10GB 的数据都加载到内存中。
4.2 计数排序（Counting Sort）
计数排序要求输入的数据必须是有确定范围的整数。将输入的数据值转化为键存储在额外开辟的数组空间中；然后依次把计数大于 1 的填充回原数组
计数排序其实是桶排序的一种特殊情况。当要排序的 n 个数据，所处的范围并不大的时候，比如最大值是 k，我们就可以把数据划分成 k 个桶。每个桶内的数据值都是相同的，省掉了桶内排序的时间。
计数排序跟桶排序非常类似，只是桶的大小粒度不一样。
public static void countingSort(int[] arr, int n) {
if (n <= 1) return;
//查找数组中数据范围
int max = arr[0];
for (int i = 1; i < n; i++) {
if (max < arr[i]) {
max = arr[i];
}
}
//申请一个计数数组count表示桶的大小, 下标大小[0, max] 下标对应arr数组元素的值
int[] count = new int[max + 1];
for (int i = 0; i <= max; i++) {
count[i] = 0;
}
//计算每个元素个数, 放入count中
for (int i = 0; i < n; i++) {
count[arr[i]]++;
}
//依次累加, count数组进行顺序累加求和
for (int i = 1; i <= max; i++) {
count[i] = count[i - 1] + count[i];
}
//临时数组temp, 存储排序之后的结果
int[] temp = new int[n];
//计数排序的关键步骤
for (int i = n - 1; i >= 0; i--) {
int index = count[arr[i]] - 1;
temp[index] = arr[i];
count[arr[i]]--;//将count中相对应个数 -1
}
//将结果拷贝给arr数组
for (int i = 0; i < n; i++) {
arr[i] = temp[i];
}
}
这种利用另外一个数组来计数的实现方式很巧妙。
计数排序只能用在数据范围不大的场景中，如果数据范围 k 比要排序的数据 n 大很多，就不适合用计数排序了。而且，计数排序只能给非负整数排序，如果要排序的数据是其他类型的，要将其在不改变相对大小的情况下，转化为非负整数。
4.3 基数排序（Radix Sort）
基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。
案例：
假设有 10 万个手机号码，将这 10 万个手机号码从小到大排序，快排时间复杂度可以做到 O(nlogn)；桶排序、计数排序，因为手机号码有 11 位，范围太大，显然不适合用这两种排序算法。
这个问题里有这样的规律：假设要比较两个手机号码 a，b 的大小，如果在前面几位中，a 手机号码已经比 b 手机号码大了，那后面的几位就不用看了。
借助稳定排序算法：先按照最后一位来排序手机号码，然后，再按照倒数第二位重新排序，以此类推，最后按照第一位重新排序。经过 11 次排序之后，手机号码就都有序了。
这里按照每位来排序的排序算法要是稳定的，否则这个实现思路就是不正确的。因为如果是非稳定排序算法，那最后一次排序只会考虑最高位的大小顺序，完全不管其他位的大小关系，那么低位的排序就完全没有意义了。
根据每一位来排序，可以用桶排序或者计数排序，它们的时间复杂度可以做到 O(n)。如果要排序的数据有 k 位，就需要 k 次桶排序或者计数排序，总的时间复杂度是 O(k*n)。当 k 不大的时候，比如手机号码排序的例子，k 最大就是 11，所以基数排序的时间复杂度就近似于 O(n)。
实际上，有时候要排序的数据并不都是等长的，比如排序牛津字典中的 20 万个英文单词，最短的只有 1 个字母，最长的有 45 个字母，中文翻译是尘肺病。对于这种不等长的数据，基数排序还适用吗？
实际上，可以把所有的单词补齐到相同长度，位数不够的可以在后面补“0”，因为根据ASCII 值，所有字母都大于“0”，所以补“0”不会影响到原有的大小顺序。这样就可以继续用基数排序了。
基数排序对要排序的数据是有要求的，需要可以分割出独立的“位”来比较，而且位之间有递进的关系，如果 a 数据的高位比 b 数据大，那剩下的低位就不用比较了。除此之外，每一位的数据范围不能太大，要可以用线性排序算法来排序，否则，基数排序的时间复杂度就无法做到 O(n) 了。
5. 选择合适的排序算法
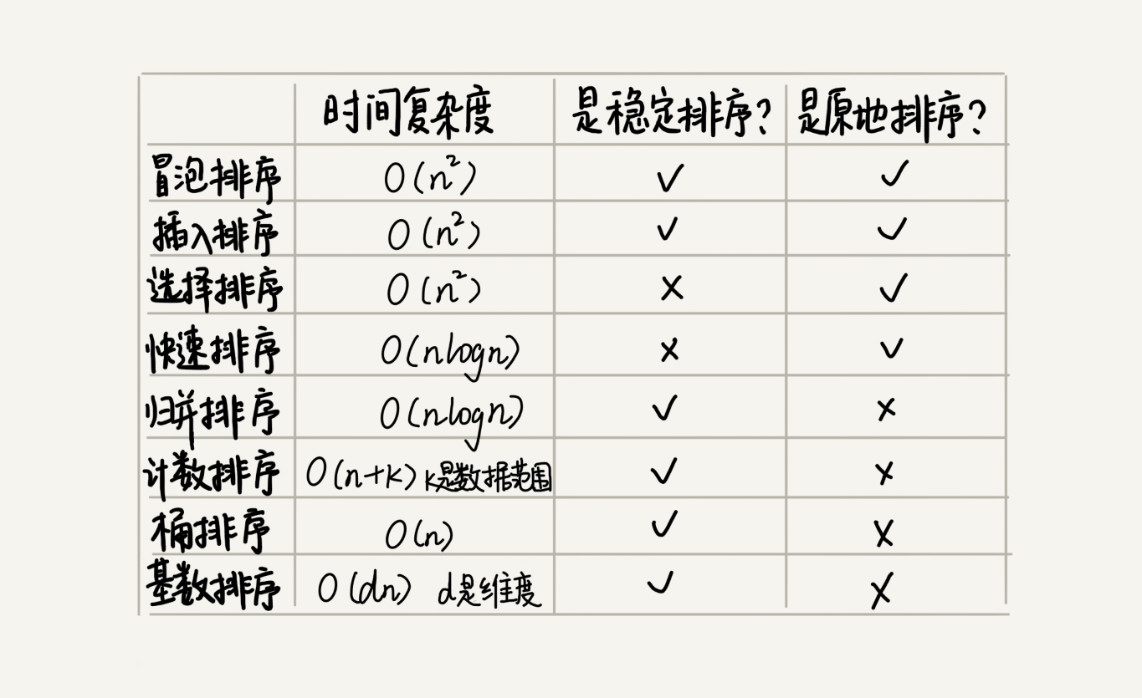
线性排序算法的时间复杂度比较低，适用场景比较特殊。要写一个通用的排序函数，不能选择线性排序算法。
如果对小规模数据进行排序，可以选择时间复杂度是 O(n2) 的算法；如果对大规模数据进行排序，时间复杂度是 O(nlogn) 的算法更加高效。所以，为了兼顾任意规模数据的排序，一般都会首选时间复杂度是 O(nlogn) 的排序算法来实现排序函数。
时间复杂度是 O(nlogn) 的排序算法不止一个，有归并排序、快速排序，堆排序。堆排序和快速排序都有比较多的应用，比如 Java 语言采用堆排序实现排序函数，C 语言使用快速排序实现排序函数。
但使用归并排序的情况并不多，快排在最坏情况下的时间复杂度是 O(n2)，而归并排序可以做到平均情况、最坏情况下的时间复杂度都是 O(nlogn)，从这点上看起来很诱人，那为什么它还是没能得到“宠信”？
归并排序的空间复杂度，归并排序并不是原地排序算法，空间复杂度是 O(n)。所以，粗略点、夸张点讲，如果要排序 100MB 的数据，除了数据本身占用的内存之外，排序算法还要额外再占用 100MB 的内存空间，空间耗费就翻倍了。
快速排序比较适合来实现排序函数，但是，快速排序在最坏情况下的时间复杂度是 O(n2)，如何来解决这个“复杂度恶化”的问题呢？
5.1 优化快速排序
如果数据原来就是有序的或者接近有序的，每次分区点都选择最后一个数据，那快速排序算法就会变得非常糟糕，时间复杂度就会退化为 O(n2)。实际上，这种 O(n2) 时间复杂度出现的主要原因还是因为我们分区点选的不够合理。
那什么样的分区点是好的分区点呢？或者说如何来选择分区点呢？
最理想的分区点是：被分区点分开的两个分区中，数据的数量差不多。
如果很粗暴地直接选择第一个或者最后一个数据作为分区点，不考虑数据的特点，肯定会出现之前讲的那样，在某些情况下，排序的最坏情况时间复杂度是 O(n2)。为了提高排序算法的性能，也要尽可能地让每次分区都比较平均。
1. 三数取中法
从区间的首、尾、中间，分别取出一个数，然后对比大小，取这 3 个数的中间值作为分区点。这样每间隔某个固定的长度，取数据出来比较，将中间值作为分区点的分区算法，肯定要比单纯取某一个数据更好。但是，如果要排序的数组比较大，那“三数取中”可能就不够了，可能要“五数取中”或者“十数取中”。
2. 随机法
随机法就是每次从要排序的区间中，随机选择一个元素作为分区点。这种方法并不能保证每次分区点都选的比较好，但是从概率的角度来看，也不大可能会出现每次分区点都选的很差的情况，所以平均情况下，这样选的分区点是比较好的。时间复杂度退化为最糟糕的 O(n2) 的情况，出现的可能性不大。
快速排序是用递归来实现的，递归要警惕堆栈溢出。为了避免快速排序里，递归过深而堆栈过小，导致堆栈溢出，
有两种解决办法：第一种是限制递归深度。一旦递归过深，超过了我们事先设定的阈值，就停止递归。
第二种是通过在堆上模拟实现一个函数调用栈，手动模拟递归压栈、出栈的过程，这样就没有了系统栈大小的限制。
查看了下Arrays.sort的源码，主要采用TimSort算法, 大致思路是这样的：
- 1 元素个数 < 32, 采用二分查找插入排序(Binary Sort)
- 2 元素个数 >= 32, 采用归并排序，归并的核心是分区(Run)
- 3 找连续升或降的序列作为分区，分区最终被调整为升序后压入栈
- 4 如果分区长度太小，通过二分插入排序扩充分区长度到分区最小阙值
- 5 每次压入栈，都要检查栈内已存在的分区是否满足合并条件，满足则进行合并
- 6 最终栈内的分区被全部合并，得到一个排序好的数组
Timsort的合并算法非常巧妙：
- 1 找出左分区最后一个元素(最大)及在右分区的位置
- 2 找出右分区第一个元素(最小)及在左分区的位置
- 3 仅对这两个位置之间的元素进行合并，之外的元素本身就是有序的
1.若数组元素个数总数小于47，使用插入排序
2.若数据元素个数总数在47~286之间，使用快速排序。应该是使用的优化版本的三值取中的优化版本。
3.若大于286的个数，使用归并排序。
- 1. 对于基本类型的数组，Java 采用的是双枢轴快速排序（Dual-Pivot Quicksort），这个算法是 Java 7 引入的。在此之前，Java 采用的是普通的快速排序，双枢轴快速排序是对普通快速排序的优化，新算法的实现代码位于类 java.util.DualPivotQuicksort 中。
- 2. 对于对象类型，Java 采用的算法是 TimSort，TimSort 算法也是 Java 7 引入的。在此之前，Java 采用的是归并排序。TimSort 算法实际上是对归并排序的一系列优化，TimSort 的实现代码位于类 java.util.TimSort 中。
- 3. 在这些排序算法中，如果数组长度比较小，它们还会采用效率更高的插入排序。
