树与堆
1.树:

树:
树是一种数据结构.
树是一种可以递归定义的数据结构.
树由n个节点组成的集合
n=0时,是空树
n>0,一个节点作为根节点,其他节点可以分为m个集合,每个集合本身又是一棵树(这就是重复单元)
节点的度:就是一个节点的子节点有多少个
树的度:整个树中最大的节点的度就是树的度
父节点:在上面紧挨着它的节点就是父节点(A是D的父节点,但是A不是H的父节点)
子节点:一个节点下面紧挨着它的节点就是它的子节点(A下面的B,C,D,E,F,G都是它的子节点)
根节点(上面没有父节点):A
叶子节点(后面不能再分叉):B,C,H,I,P,Q,K,L,M,N,或者说度为0的节点就叫叶子节点
树的深度(高度):根到叶子最长的节点个数(就是最多几层)
子树:EIJPQ就是个子树
用树模拟文件系统:
class Node:#创建文件夹,这里暂时没有创建文件的功能 def __init__(self,name,type='dir'): self.name=name self.type=type #'dir' or 'file' self.children=[] self.parent=None #链式存储 def __repr__(self): return self.name class FileSystemTree: def __init__(self): self.root=Node('/') self.now=self.root def mkdir(self,name):#创建文件夹 #name以/结尾 if name[-1] != '/': name+='/' node=Node(name) self.now.children.append(node) node.parent=self.now def ls(self):#展示文件夹下所有文件 return self.now.children def cd(self,name):#进入某个文件夹 if name[-1] != '/': name+='/' if name=='../': #返回上一级目录了 self.now=self.now.parent return for child in self.now.children: if child.name==name: self.now=child return raise ValueError('invalid dir') tree =FileSystemTree() tree.mkdir('var/') tree.mkdir('usr/') tree.mkdir('bin/') print(tree.root.children)#[var/]返回文件名 tree.cd('bin/') tree.mkdir('python/') tree.cd('../') print(tree.ls())
二叉树:
度不超过2的树(整个树中每个节点最多有连个孩子节点,分别为左孩子节点和右孩子节点)就是二叉树
满二叉树:
一个二叉树,如果每一层的节点数都达到最大值,则这个二叉树就是满二叉树.
如图:

完全二叉树:
叶子节点只能出现在最下层和次下层,并且最下面一层的节点都集中在该层最左边的若干位置的二叉树
如图:
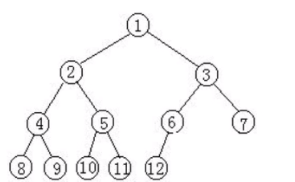
二叉树的顺序存储方式:
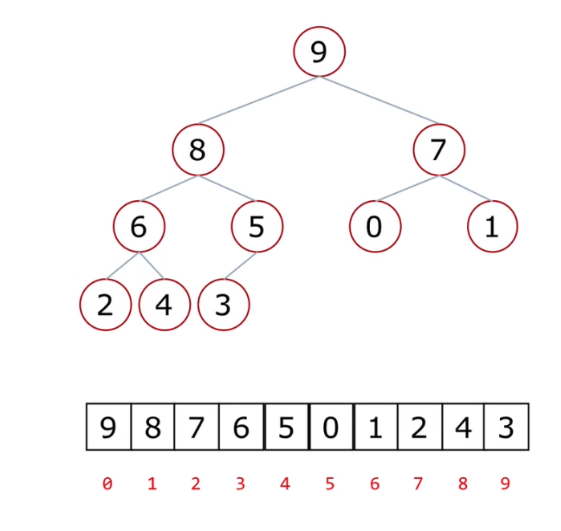
节点的索引下标用红字写在上面了
看一下父节点(假设是i)的下标与左右孩子结点的关系
所有左节点的下标都是2i+1(可以试i=0,1,2,3得到的索引全是左下标)

所有右节点的下标都是2i+2

只要知道父节点就可以算出左和右的子节点
知道到左右节点的索引后都可以直接减一再底板除(//)来得到父节点的索引(底板除得到小数后向下取整,不会四舍五入)
二叉树的链式存储方式:
将二叉树的节点定义为一个对象,节点之间通过类似链表的链接方式来连接
如图:
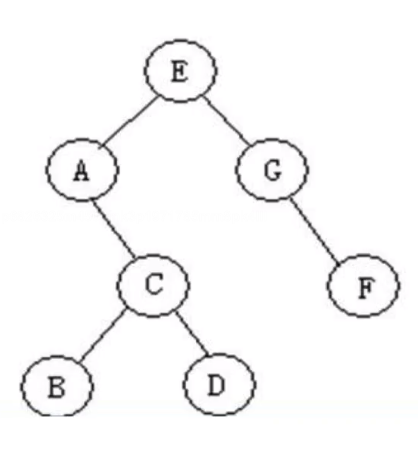
代码如下:
class BiTreeNode: def __init__(self,data): self.data=data self.lchild=None #左孩子 self.rchild=None #右孩子 a=BiTreeNode('A') b=BiTreeNode('B') c=BiTreeNode('C') d=BiTreeNode('D') e=BiTreeNode('E') f=BiTreeNode('F') g=BiTreeNode('G') e.lchild=a e.rchild=g a.rchild=c c.lchild=b c.rchild=d g.rchild=f root=e print(root.lchild.rchild.data) #输出:C
链式存储的遍历
共四种遍历
注意:
这四种遍历分类:
深度优先:
①前序遍历
②中序遍历
③后序遍历
广度优先:
①层次遍历
①前序遍历:
先父节点,再左子树,再走右子树,保证每一层都是'父左右'这样的结构
def pre_order(root):#前序遍历,先父节点,再左子树,再走右子树,保证每一层都是'父左右'这样的结构 if root : print(root.data,end=',') pre_order(root.lchild) pre_order(root.rchild) pre_order(root) #输出:E,A,C,B,D,G,F,
②中序遍历:
父节点在中间,左边是左子树递归的,右边是右子树递归的,保证每一层都是'左父右'这样的结构
def in_order(root):#中序遍历,父节点在中间,左边是左子树递归的,右边是右子树递归的,保证每一层都是'左父右'这样的结构(有点像快排,找中位数,中位数就是父节点) if root: in_order(root.lchild) print(root.data,end=',') in_order(root.rchild) in_order(root) #输出:A,B,C,D,E,G,F,
③后序遍历:
先左子树,后右子树,最后是父节点,保证每一层都是'左右父'这样的结构
def post_order(root): #后序遍历,先左子树,后右子树,最后是父节点,保证每一层都是'左右父'这样的结构 if root: post_order(root.lchild) post_order(root.rchild) print(root.data,end=',') post_order(root) # 输出:B,D,C,A,F,G,E,
注意:以上三种序列,至少给两个,才能唯一确定一种树,否则只给一种顺序,会有多种树的结构
④层次遍历:
(利用队列),多叉树也适用
按照从跟到叶子节点,每一层节点都是从左到右出来的。
from collections import deque def level_order(root): queue=deque() queue.append(root) while len(queue)>0:#只要队不为空 node=queue.popleft()#出队 print(node.data,end=',') if node.lchild: queue.append(node.lchild) if node.rchild: queue.append(node.rchild) level_order(root) #E,A,G,C,F,B,D,
二叉搜索树:
一个二叉树,满足:假设x是二叉树的一个节点,y是x的左子树的一个节点,z是x的右子树的一个节点,那么一定有y.key<=x.key和z.key>=x.key
class BST: def __init__(self,li=None):#传个列表进来 self.root=None if li:#传个列表进来,列表是非空,就把列表内容都插入二叉搜索树中 for val in li: self.insert_no_rec(val) #插入 写法一: 递归写法 def insert(self,node,val):#插入操作:node是要插入的二叉树的根节点,val是要插入的节点的值 if not node:#节点不存在,就新创建一个节点 node =BiTreeNode(val) elif val < node.data: #如果节点存在,就看传进来时从根节点向下一个一个的比较大小,如果val比较小,就一直往左走 node.lchild=self.insert(node.lchild,val) node.lchild.parent=node elif val>node.data:#如果val值比较大,就一直往右走 node.rchild=self.insert(node.rchild,val) node.rchild.parent=node return node #插入 写法二: 非递归写法,速度比较快 def insert_no_rec(self,val): p=self.root if not p:#如果是个空树 self.root=BiTreeNode(val) return while True: #如果不是空树 if val <p.data:#如果val小于这个节点的值,就往左孩子上插 if p.lchild:#如果左孩子存在 p=p.lchild#原来和val比大小的节点就移动到他左孩子上,让左孩子和val比大小 else:#如果做孩子不存在 p.lchild=BiTreeNode(val)#就直接把val实例化出个对象,放到左孩子的位置上 p.lchild.parent=p return elif val>p.data:#如果val大于比较的这个节点的值,那就让val和他的右孩子比大小 if p.rchild: p=p.rchild else: p.rchild=BiTreeNode(val) p.rchild.parent=p return else:#val和根节点的值相同,就不动了 return # 查询 写法一:递归版本 def query(self,node,val): if not node: return None if node.data<val: return self.query(node.rchild,val) elif node.data>val: return self.query(node.lchild, val) else: return node # 查询 写法二:非递归版本 def query_no_rec(self,val): p=self.root while p: if p.data<val: p=p.rchild elif p.data>val: p=p.lchild else: return p return None # 三种遍历: def pre_order(self,root):#前序遍历 if root : print(root.data,end=',') self.pre_order(root.lchild) self.pre_order(root.rchild) def in_order(self,root):#中序遍历,中序出来的结果一定是从小到大排好序的 if root: self.in_order(root.lchild) print(root.data,end=',') self.in_order(root.rchild) def post_order(self,root): #后序遍历 if root: self.post_order(root.lchild) self.post_order(root.rchild) print(root.data,end=',') #插入测试 tree=BST([1,3,10,0,9,6,4,2,8,7,5]) tree.pre_order(tree.root) #1,0,3,2,10,9,6,4,5,8,7, print('') tree.in_order(tree.root)#而中序出来的一定是按从小到大排好序的(左父右) #0,1,2,3,4,5,6,7,8,9,10, print('') tree.post_order(tree.root) #0,2,5,4,7,8,6,9,10,3,1, #查询测试 import random li=list(range(0,500,2))#全是偶数 random.shuffle(li) tree=BST(li) print(tree.query_no_rec(3))#3是偶数不存在的这个二叉树中 #None print(tree.query_no_rec(4)) #<__main__.BiTreeNode object at 0x038EC510> print(tree.query_no_rec(4).data) #4
2.堆:
一种特殊的完全二叉树结构
大根堆:
一棵完全二叉树,满足任一节点都比孩子节点大

小根堆:
一棵完全二叉树,满足任一节点都比其孩子节点小
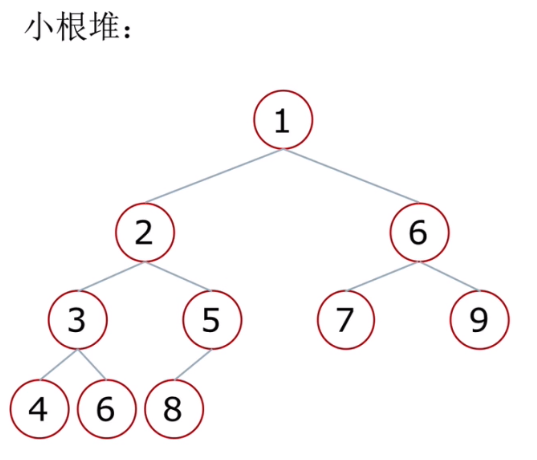
堆的向下调整:
堆整体不是个跟堆,但是左子树是个大根堆或小根堆,右子树是个大根堆或者小根堆(左右要保持一致都是大根堆或者都是小根堆)
这时可以通过向下调整使得整个跟堆变成一个大根堆或者小根堆
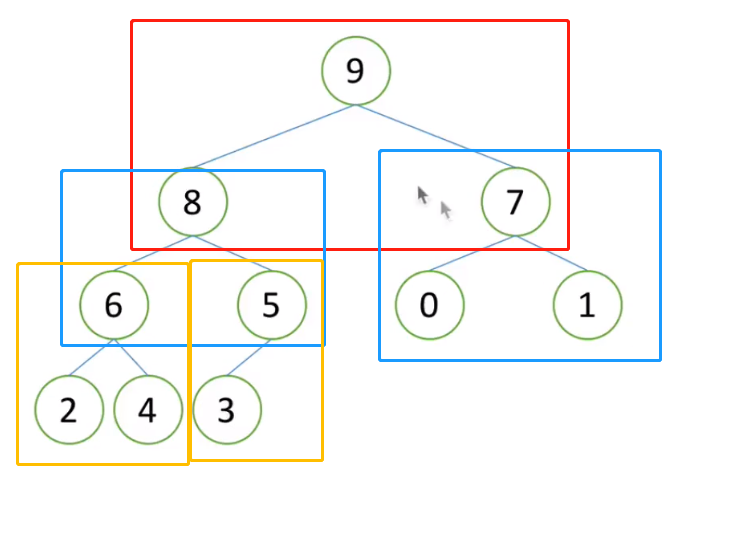
如图,左右都是大根堆,但是整体不是大根堆,此时要把2向下调整

调整后:整体是个大根堆

堆排序:
时间复杂度:O(nlogn)
推算:
sift是logn,这个函数每次运行时走的是树的高度,每次都折半,不是左就是右,所以是logn
heap_sort是n或n/2,里面又套了sift,所以就是nlogn
步骤:
1.建立堆
2.得到堆顶元素,为最大元素
3.去掉堆顶,将堆最后一个元素(叶子结点最右边的元素,上图中3就是最后一个元素)放到堆顶,此时可以通过一次调整(向下调整)重新使堆有序
4.堆顶元素为第二大元素
5.重复步骤3,直到堆为空
代码:
步骤:先建大根堆,再从下到上循环每个父节点(自下而上就不怕你向下取循环,因为之前的都已经循环过了,最大的数字一定在上面),造出大根堆,
最后取根节点值与最后一个索引位置交换,再用sift方法从头到尾n-2..直到0,一个一个地与根节点值进行交换,交换后的最后面的索引的值就是当前列表的最大值(排序就一点一点的按照列表的顺序来了).
# 堆排序(没用递归) #第一步:调整三个节点:父节点和左右子节点,使其成为大根堆,如果while能一直向下循环,那么这次操作就是一次向下循环 def sift(li, low, high): """ :param li: 列表 :param low: 堆的根节点位置 :param high: 堆的最后一个元素的位置,high是最后一个数字的索引,超了high就不存在了 :return: """ i = low # i最开始指向根节点,根节点数字的索引 j = 2 * i + 1 # j开始是左孩子,j是i的左孩子的索引 tmp = li[low] # 把堆顶存起来 while j <= high: # 只要j位置有数 #如果右孩子节点存在,就和左孩子节点比较大小,把大的值放到l[j]中 if j + 1 <= high and li[j+1] > li[j]: # 如果右孩子有并且右孩子比左孩子大,j + 1 <= high保证右孩子不超索引范围 j = j + 1 # j指向右孩子 #如果子节点中最大值大于父节点的值,那就将父节点的值改成最大的子节点的值,此时i指的是父节点的索引,l[j]是三个节点中的最大值 if li[j] > tmp: #子节点找到了最大的li[j],他要和根节点(如果不在顶层就是父节点了)的数字比大小,大的放在根节点 li[i] = li[j] i = j # 往下看一层,相当于i+=1,i向下走了一层,j也就向下走一层,找到了下一层的左孩子 j = 2 * i + 1 #如果前面两个if都不成立,那么父节点(tmp)的值就是三个节点中最大的了 else: # tmp更大,把tmp放到i的位置上 li[i] = tmp # 把tmp放到某一级领导位置上 break #如果j超过了索引范围,那么此时i就指到了叶子节点(也就是最后一行了),那么就证明tmp是最小的,就把tmp放到最后一行空着的的叶子节点(li[i])即可 else:#此时j>high,而i到了最后一行了,就把tmp放到最后一行的子叶了 li[i] = tmp # 把tmp放到叶子节点上 #建堆+出列表 def heap_sort(li): n = len(li) # 循环所有父节点建堆(重点:倒序循环父节点,从最下面的父节点开始循环) for i in range((n-2)//2, -1, -1): #先从最后一个节点的父节点开始循环, # 最后一个节点假设是i,它的父节点就是(i-1)//2这是固定的算法,不管是左子节点还是右子节点, # 现在最后一个数字索引是n-1,那么他的父节点就是(n-2)//2 # i表示建堆的时候调整的部分的根的下标,每次i都是一个父节点,调整的是他的子树(只包含自己的两个子节点) #这里是从(n-2)//2遍历到0(顾头不顾尾),倒序(-1) sift(li, i, n-1) #这里n-1一直指代这个堆的最后一个叶子节点, # 其实他应该变化,每次都应该指该子树的右子节点, # 但是这个不容易求,n-1肯定比其他子树的右子节点大,用它限制肯定会多算几步,但是一定不会错 # 建堆完成了(是按照堆的顺序排的数字) print('跟堆建成:',li)#现在出来的列表是按照堆的顺序拿出来的,还要最后排一下序 #按照列表的顺序排序() for i in range(n-1, -1, -1): #这里可以改写成(n-1,0,-1),顾头不顾尾,所以0这一次不会继续循环了,到1就结束了,到最后一个元素0索引时,下一步自己和自己交换就没意思了,所以我个人认为可以吧-1换成0 # i 每次取值都是指向当前堆的最后一个元素 #从n-1遍历到0,每次步长是-1,就相当于是列表从最右端每次都向最左端挪一位 li[0], li[i] = li[i], li[0] sift(li, 0, i - 1) #i-1是新的high,i指的是最后一个数字,他现在放的是根节点那个最大数字, # 循环一次就相当于最大值找到了,再循环一次就又找了个第二大的 li = [i for i in range(100)] import random random.shuffle(li) print('手动建的乱序表:',li) heap_sort(li) print('排序后的结果:',li)
sift的操作就是自上而下把每三个节点(父节点,左右子节点)都组成大根堆
注意:如果你不确定你这个堆整体是大根堆,你从根节点开始,用sift方法最后得到的不一定是大根堆,因为最大的数字不一定在最上面三个节点里面出现.
python中有对排列模块heapq:
import heapq #q表示queue队列的意思 实现优先队列(优先小的先出或者大的先出) import random li = list(range(100)) random.shuffle(li) print(li)#新建的乱序列表 heapq.heapify(li) #建堆,这里python模块默认建的是小根堆 n=len(li) lst=[] for i in range(n): # print(heapq.heappop(li), end=' ')#小根堆,每次都弹出最小的 lst.append(heapq.heappop(li)) print(lst)
堆排序的topk问题:
topk问题:列表有n个数字,从大到小排序,我取前k大的数字
应用场景:微博热搜问题,不需要存数据库,因为很多,而且时间间隔不长,经常会更换.
解决思路:
①先排序(快排),后切片 时间复杂度(最大):O(nlogn+k) 当k<n时k可以省略.O(nlogn)
②冒泡/选择/插入,排序后再切片, 时间复杂度(第二大): O(kn)
实现步骤(堆排序思路):
①取列表前k个元素,并建立一个小根堆,堆顶就是列表中第k大的数字
②从k往后依次遍历原来的列表,取出一个数字就和堆顶的数字比大小,如果堆顶的数字较大,那循环继续往下走,不做任何操作,如果你从原列表取的数字大于堆顶的数字,那就将他替换堆顶的数字,并对这k个元素组成的堆进行调整,使之成为一个新的小根堆.
③当你从k+1直到遍历完原列表,,你得到了一个小根堆,这个小根堆就是前k大的数字,你再像堆排序最后出数那样倒序弹出堆顶的数字(因为现在是小根堆,堆顶数字是这里面最小的)
代码:
def sift(li, low, high): i = low j = 2 * i + 1 tmp = li[low] while j <= high: if j + 1 <= high and li[j+1] < li[j]:#注意这里要建小根堆,使大的数字都在下面 j = j + 1 if li[j] < tmp: #注意这里要建小根堆,使大的数字都在下面 li[i] = li[j] i = j j = 2 * i + 1 else: break li[i] = tmp def topk(li, k): heap = li[0:k] # 1.建堆 for i in range((k-2)//2, -1, -1): sift(heap, i, k-1) # 2.遍历原列表k以外的元素(k到n-1)注:k以外的第一个元素的索引是k,最终得到的小根堆只包含前k大的数字 for i in range(k, len(li)): if li[i] > heap[0]: heap[0] = li[i] sift(heap, 0, k-1) # 3.出数(前k大的数字已经拿好了都在heap里面了,都在小根堆上,现在是要排序了) for i in range(k-1, -1, -1): #这里可以改写成(k-1,0,-1),因为最后一次是heap[0]和自己交换,没意义,所以就到1时就结束了(range顾头不顾尾) heap[0], heap[i] = heap[i], heap[0] sift(heap, 0, i - 1) return heap#你要的数字已经存到了heap里面了 import random li = list(range(200)) random.shuffle(li) print(topk(li, 10))#我取前10个大的数字

