数据结构中的顺序表和链表(Python语言)

转载：https://blog.csdn.net/weixin_43187669/article/details/96426362

算法是为了解决实际问题而设计的，数据结构是算法需要处理的问题载体。

Python提供现成的数据结构类型叫做Python的内置数据结构，比如列表、元组、集合、字典。
Python系统里面没有直接定义需要自定义的成为Python的扩展数据结构，比如栈、队列等。

顺序表的基本形式
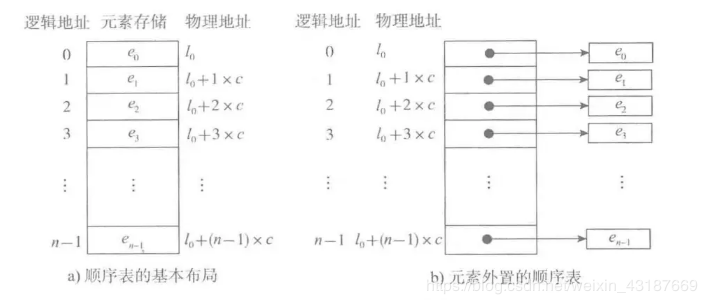
1.定义：所谓顺序表，就是将元素顺序地存放在一块连续的存储区里，元素间的顺序关系由他们的存储顺序自然表示。

图a，每个元素所占存储单元大小固定相同。
图b，每个元素所占的存储单元大小不相同。存储一个链接地址。

顺序表的结构与实现

顺序表的两种基本实现方式
图a为一体式结构，存储表信息的单元与元素存储区以连续的方式安排在一快存储区里。
图b为分离式结构，存储表信息的单元与元素存储区以连续的方式安排在两块存储区里。

元素存储区替换
一体式结构：若想更换数据区，则只能整体搬迁，即整个顺序表对象改变了。
分离式结构：若想更换数据区，只需要将信息区中的数据区链接地址更新即可，而该顺序表对象不变。

元素存储区扩充
1.只有分离式结构的元素存储区可以扩充。
2.扩充的两种策略：
1）每次扩充增加固定数目的存储位置，如每次扩充增加10个元素位置。
特点：节省空间，但是扩充操作频繁，操作次数多。
2）每次扩充容量加倍，如每次扩充增加一倍存储空间。
特点：减少了扩充操作的执行此书，但可能会浪费空间资源。以空间换时间，推荐此方式。

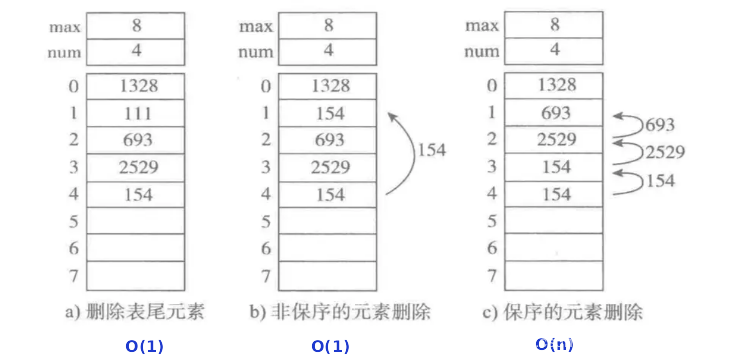
顺序表的操作
1.增加元素的三种方式。

Python中的顺序表
Python中的list和turple两种类型采用了顺序表的实现技术。
list是可变类型，即采用分离式技术实现的动态顺序表。
turple是不可变型，即不变的顺序表。

list的基本丝线技术
1.Python标准类型list就是一种元素个数可变的线性表，可以加入和删除元素，具有以下特征：(1)顺序表：基于下标的高效元素访问和更新，时间复杂度是O(1);
(2)分离式技术：允许任意加入元素，而且在不断加入元素的过程中，表对象的id不变。

list元素存储区扩充规则
1.在建立空表（或者很小的表）时，系统分配一块能容纳8个元素的存储区；
2. 在执行插入操作（insert或append）时，如果元素存储区满就换一块4倍大的存储区。
3. 如果此时的表已经很大（目前的阀值为50000），则改变策略，采用加一倍的方法。
原因: 为了避免出现过多空闲的存储位置。

链表
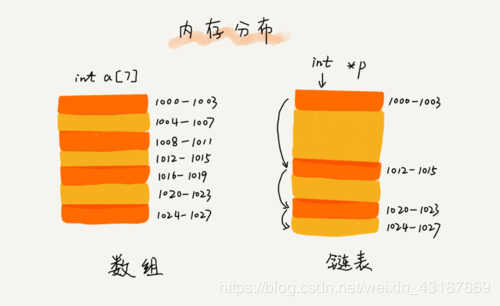
顺序表的构建需要预先知道数据大小来申请连续的存储空间，而在进行空充时又需要进行数据的搬迁，所以使用起来并不是很灵活，但是链表结构可以充分利用计算机的内存空间，实现灵活的内存动态管理。

1.链表的定义：链表是一种常见的基础书籍结构，是一只种类线性表，但是不想顺序表一样连续存储数据，而是在每一个节点（数据存储单元）里存放下一个节点的位置信息。（即地址）

单链表

1.单链表的定义：单向链表也叫单链表，每个节点包含两个域，一个信息域（元素域）和一个链接域。这个链接指向链表中的下一个节点，而最后一个节点的链接域则指向一个空值。

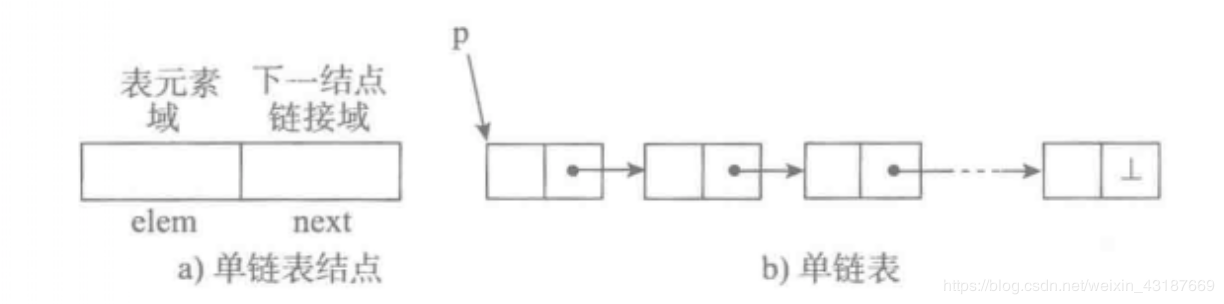
2.节点实现：

class SingleNode(object):
    """单链表的节点“”“
    def ——init——（self，item）：
        #item存放数据元素
        self。item = item
        #next是下一个结点的标示
        self.

 

3.单链表的操作

length() 链表长度

travel() 遍历整个链表

add(item) 链表头部添加元素

append(item) 链表尾部添加元素

insert(pos, item) 指定位置添加元素

remove(item) 删除节点

search(item)查找节点是否存在

is_empty() 链表是否为空

 

4.单链表的头部添加元素与尾部添加元素

 

5.单链表在指定位置添加元素

6.删除节点

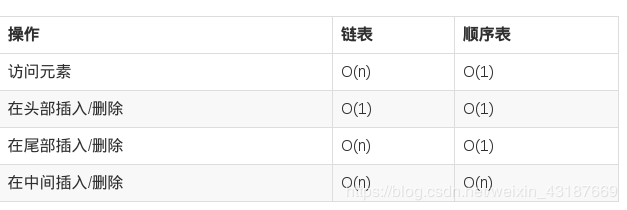
链表与顺序表的对比：

单向循环链表

1.单链表的一个变形是单向循环链表，链表中最后一个节点的next域不再为None，而是指向链表的头节点。

2.单向链表的操作及其实现：
函数名 功能
length() 链表长度
travel() 遍历整个链表
add(item) 链表头部添加元素
append(item) 链表尾部添加元素
insert(pos, item) 指定位置添加元素
remove(item) 删除节点
search(item) 查找节点是否存在
is_empty() 链表是否为空

双向链表
特点：每个节点有两个链接：一个指向前一个节点，当此节点为第一个节点时，指向空值；而另一个指向下一个节点，当此节点为最后一个节点时，指向空值。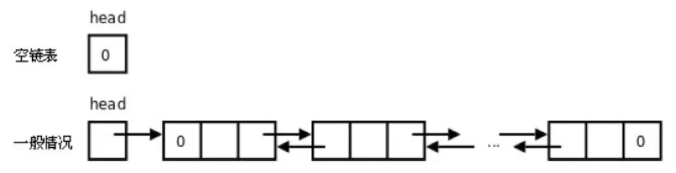

指定位置添加节点算法示意图：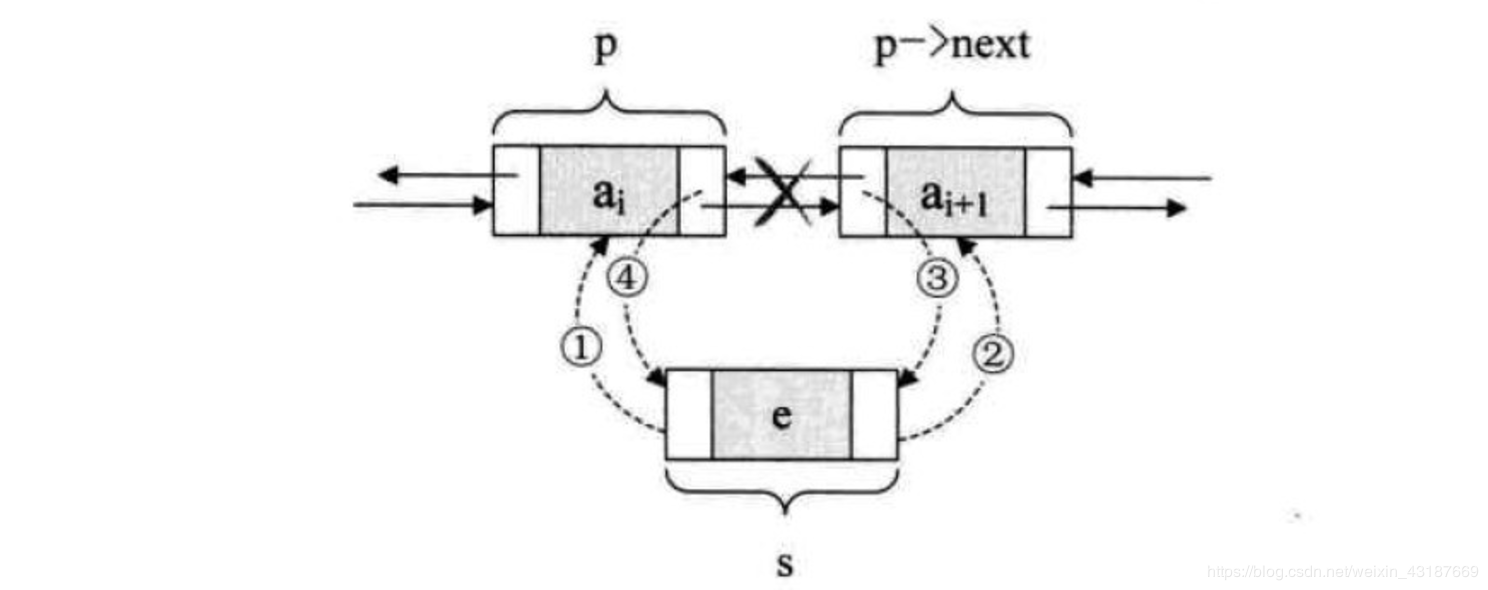

2.删除元素算法示意图：

class Node(object):
def __init__(self, element):
    self.element = element
    # 数据域
    self.next = None
    self.prev = None

def __str__(self):
    return self.elelemnt


class DuLinkList(object):
def __init__(self):
    self.head = None

def is_empty(self):
    return self.head == None
#判空
def __len__(self):
    if self.is_empty():
        return 0
    cur = self.head
    linkLen = 0
    while cur:
        cur = cur.next
        linkLen += 1
    return linkLen
#计算长度
def travel(self):
    if not self.is_empty():
        cur = self.head
        while cur.next != None:
            print(cur.element, end=',')
            cur = cur.next
        print(cur.element)
    else:
        print('空链表')
#遍历每个元素
def add(self, item):
    node = Node(item)
    if self.is_empty():
        self.head = node
    else:
        node.next = self.head
        self.head.prev = node
        self.head = node
#在链表头部添加节点
def append(self, item):
    node = Node(item)
    if self.is_empty():
        self.head = node
    else:
        cur = self.head
        while cur.next != None:
            cur = cur.next
        cur.next = node
        node.prev = cur
#在链表尾部添加节点
def insert(self, index, item):
    if index <= 0:
        self.add(item)
    elif index >= len(self):
        self.append(item)
    else:
        node = Node(item)
        count = 0
        cur = self.head
        while count <= index - 1:
            count += 1
            cur = cur.next
        node.next = cur.next
        cur.next = node
        node.prev = cur
#插入节点
def remove(self,item):
    pre = None
    cur = self.head
    if cur.element == item:
        self.head = self.head.next
    else:
        while cur:
            if cur.element != item:
                pre = cur
                cur = cur.next
            else:
                pre.next = cur.next
                cur.prev = pre.next
                break
#删除节点

if __name__ == '__main__':
link = DuLinkList()
print("链表长度：", len(link))
link.travel()
print('链表是否为空？', link.is_empty())
print('添加头结点：')
for item in range(5):
    link.append(item)
print('链表长度：', len(link))
link.insert(1, 'python')