假设检验的Python实现

结合假设检验的理论知识，本文使用Python对实际数据进行假设检验。

导入测试数据

从线上下载测试数据文件，数据链接：https://pan.baidu.com/s/1t4SKF6U2yyjT365FaE692A*
数据字段说明：

gender：性别，1为男性，2为女性
Temperature:体温
HeartRate：心率

下载后，使用pandas的read_csv函数导入数据。

import numpy as np
import pandas as pd
from scipy import stats

test_df = pd.read_csv('test.csv')

问题清单

针对此测试数据，提出以下问题：

1. 人体体温的总体均值是否为98.6华氏度？
2. 人体的温度是否服从正态分布?
3. 人体体温中存在的异常数据是哪些？
4. 男女体温是否存在明显差异？
5. 体温与心率间的相关性(强？弱？中等?)

解题步骤

1. 体温的总体均值是否为98.6华氏度？

解法1：
此问题可以转化为假设检验问题，可以假设：
$H_0: \mu = 96.8 \( \)H_1: \mu \neq 96.8 $

这是一个双侧检测问题，所以只要\(\mu>\mu_0\)或\(\mu<\mu_0\)二者之中有一个成立，就可以拒绝原假设。

根据人大《统计学》第7版p163：

在样本量大的条件下，如果总体为正态分布，则样本统计量服从正态分布；如果总体为非正态分布，则样本统计量渐近服从正态分布。在这些情况下，我们都可以把样本统计量视为正态分布，这时可以使用\(z\)统计量。

本题中，总体标准差\(\sigma\)未知，可以用样本标准差\(s\)代替。

## 计算Z统计量
mu = 96.8
temp = test_df['Temperature']
# 样本均值
sample_mean = np.mean(temp)

# 样本方差
sample_std = np.std(temp, ddof=1)
# 样本个数
sample_size = temp.size

z = (sample_mean-mu)/(sample_std/np.sqrt(sample_size))
print(z)
22.537033076347175

按照双侧检验的原理，在显著性水平\(\alpha=0.05\)情况下
\(z_{\frac{\alpha}{2}}=\pm 1.96\)
因为\(|z|>|z_{\frac{\alpha}{2}}|\)，所以拒绝原假设，人体体温的总体均值不是98.6华氏度。

解法2：
可以直接使用statsmodels包的statsmodels.stats.weightstats.ztest函数直接执行计算，http://www.statsmodels.org/stable/generated/statsmodels.stats.weightstats.ztest.html
用法如下：

statsmodels.stats.weightstats.ztest(x1, x2=None, value=0, alternative='two-sided', usevar='pooled', ddof=1.0)[source]

2. 人体的温度是否服从正态分布?

解法：

参考Python验证数据的抽样分布类型，先画出分布的直方图，然后使用scipy.stat.kstest函数进行判断。

%matplotlib inline
import seaborn as sns
sns.distplot(temp, color='b', bins=10, kde=True)

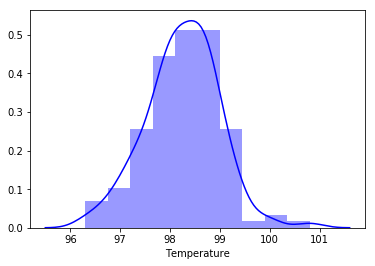
简单从图形看，大于99.3之后的数据分布极少。初步认为不符合正态分布。

然后使用kstest验证。

In: stats.kstest(temp, 'norm')
Out: KstestResult(statistic=1.0, pvalue=0.0)

可以发现pvalue<0.05，即认为体温不符合正态分布。

判断是否服从t分布:

In: np.random.seed(1)
    ks = stats.t.fit(temp)
    df = ks[0]
    loc = ks[1]
    scale = ks[2]
    t_estm = stats.t.rvs(df=df, loc=loc, scale=scale, size=sample_size)
    stats.ks_2samp(temp, t_estm)
Out: Ks_2sampResult(statistic=0.11538461538461536, pvalue=0.33281734591562734)

此处的思路是先用t分布拟合区域收入均值，然后使用ks_2samp函数比较区域收入均值和t分布的随机变量。因为pvalue大于0.05，认为该数据集服从t分布。

判断是否服从卡方分布:

In: np.random.seed(1)
    chi_square = stats.chi2.fit(temp)
    df = chi_square[0]
    loc = chi_square[1]
    scale = chi_square[2]
    chi_estm = stats.chi2.rvs(df=df, loc=loc, scale=scale, size=sample_size)
    stats.ks_2samp(temp, chi_estm)
Out: Ks_2sampResult(statistic=0.07692307692307687, pvalue=0.8215795712396048)

pvalue为0.82，说明体温数据更服从卡方分布。可以使用以下方式，画出拟合的卡方分布和测试数据的对比图。

from matplotlib import pyplot as plt
plt.figure()
temp.plot(kind = 'kde')
chi2_distribution = stats.chi2(chi_square[0], chi_square[1],chi_square[2])
x = np.linspace(chi2_distribution.ppf(0.01), chi2_distribution.ppf(0.99), 100)
plt.plot(x, chi2_distribution.pdf(x), c='orange')
plt.xlabel('Human temperature')
plt.title('temperature on chi_square', size=20)
plt.legend(['test_data', 'chi_square'])

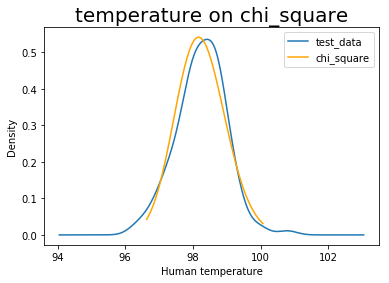
3. 人体体温中存在的异常数据是哪些？

解法：

已知体温数据服从卡方分布的情况下，可以直接使用Python计算出P=0.025和P=0.925时的分布值，在分布值两侧的数据属于小概率，认为是异常值。

In: chi2_distribution.ppf(0.025)
Out:97.0690523831819
In: chi2_distribution.ppf(0.925)
Out:99.332801136025
In: temp[temp<97.069]
Out:0     96.3
    1     96.7
    2     96.9
    3     97.0
    65    96.4
    66    96.7
    67    96.8
    Name: Temperature, dtype: float64
In: temp[temp>99.332]
    63      99.4
    64      99.5
    126     99.4
    127     99.9
    128    100.0
    129    100.8
    Name: Temperature, dtype: float64

4. 男女体温是否存在明显差异？

解法：

此题是一道两个总体均值之差的假设检验问题，因为是否存在差别并不涉及方向，所以是双侧检验。建立原假设和备择假设如下：

\(H_0: \mu_1 - \mu_2 = 0\) 没有显著差别

\(H_1: \mu_1 - \mu_2 \ne 0\) 有显著差别

由于\(\sigma_1^2\),\(\sigma_2^2\)未知，也无法断定\(\sigma_1^2=\sigma_2^2\)是否成立，且\(n_1\),\(n_2\)的数量为65。

In: test_df.groupby(['Gender']).size()
Out:Gender
    1    65
    2    65
    dtype: int64

在此样本量情况，抽样分布近似服从自由度为f的t分布，其中f为：

\[f=\frac{(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2})^2}{\frac{(\frac{s_1^2}{n_1})^2}{n_1-1}+\frac{(\frac{s_2^2}{n_2})^2}{n_2-1}} \]

检验统计量t的计算公式为：

\[t = \frac{(\bar{x_1}-\bar{x_2})-(\mu_1-\mu_2)}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n2}}} \]

male_df = test_df.loc[test_df['Gender'] == 1]
female_df = test_df.loc[test_df['Gender'] == 2]

• 方法一：构建统计量计算函数

def cal_f(a, b):
     n_1 = len(a)
     n_2 = len(b)
     mean_1 = a.mean()
     mean_2 = b.mean()
     std_1 = a.std()
     std_2 = b.std()

     s_1 = std_1**2/n_1
     s_2 = std_2**2/n_2
     f = (s_1 + s_2)**2 / (s_1**2/(n_1 - 1) + s_2**2/(n_2 -1))
     print('degree of freedom=%.3f', % f)

     t = (mean_1 - mean_2)/np.sqrt(s_1 + s_2)
     
     # 计算边界值，设置显著性水平为0.05，双侧检验，取边界值为0.025
     v = stats.t.ppf(0.025, f)

     print('stat=%.3f, boudary=%.3f' % (t, v))

     if abs(t)>abs(v):
       print("拒绝原假设，男女体温存在明显差异。")
     else:
       print("不能拒绝原假设，男女体温无明显差异。")

调用自定义函数

In: cal_f(male_df['Temperature'],female_df['Temperature'])
Out:degree of freedom=127.510
    stat=-2.285, boudary=-1.979
    拒绝原假设，男女体温存在明显差异。

• 方法2，使用ttest_ind函数1

stats.t.ppf(0.025, 127.51)
stat, p = stats.ttest_ind(male_df['Temperature'],female_df['Temperature'])
print('stat=%.3f, p=%.3f' % (stat, p))
if p > 0.05:
	print('不能拒绝原假设，男女体温无明显差异。')
else:
	print('拒绝原假设，男女体温存在明显差异。')
    
Out：
stat=-2.285, p=0.024
拒绝原假设，男女体温存在明显差异。

注意：此函数计算得出的p值为双侧概率的累加，所以直接与显著性水平0.05进行比较。可以用以下方式证明是双侧概率：

# 将方法1中的统计值代入t分布的概率分布
In: stats.t.cdf(stat, 127.51)
Out:0.011969134059074056

上述结果正好是双侧概率的一半。

5. 体温与心率间的相关性

可以使用皮尔逊相关性系数2检验两组数据之间的关系。在处理前，可以先用散点图展示下两者在二维空间上的分布。

heartrate_s = test_df['HeartRate']
temperature_s = test_df['Temperature']
from matplotlib import pyplot as plt
plt.scatter(heartrate_s, temperature_s)

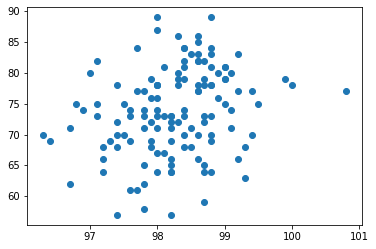
计算皮尔逊相关系数3：

In: stat, p = stats.pearsonr(heartrate_s, temperature_s)
    print('stat=%.3f, p=%.3f' % (stat, p))
Out:stat=0.254, p=0.004

已知皮尔逊相关系数为0，数据无相关性，而大于0表示有正相关性，当为1时完全正相关。因为结果为0.004，体温和心率之间可以认为基本无相关性。从图形上也可以发现四散分布，缺乏相关性。

参考资料

欢迎扫描二维码进行关注