论文阅读笔记:斯坦福大学SNAP团队《图信息瓶颈》—— Graph Information Bottleneck
论文:Tailin Wu, Hongyu Ren, Pan Li, Jure Leskovec. Graph Information Bottleneck. In NIPS 2020.
概要:图神经网络(GNNs)是一种融合网络结构和节点特征信息的表示学习方法,容易受到对抗性攻击。本文提出了一个信息论原则——图信息瓶颈(Graph Information Bottleneck,GIB),它能够优化图数据表示的表达能力和鲁棒性之间的平衡。GIB继承了一般信息瓶颈(Graph Information Bottleneck,IB)的思想,通过最大化表示与目标之间的互信息,同时约束表示与输入数据之间的互信息,来学习给定任务的最小充分表示。GIB与一般IB不同之处在于其对结构信息和特征信息进行了正则化处理。本文给出了两种结构正则化的抽样算法,并用两种新模型GIB-Cat和GIB-Bern对GIB原理进行了举例说明,并通过评估GIB-Cat和GIB-Bern的抗攻击能力来说明其优点。实验证明了我们提出的模型比最新的图防御模型更健壮。基于GIB的模型在对抗性扰动图结构和节点特征的情况下,与基准方法相比达到了31%的提升。
一般深度学习中的信息瓶颈
给定输入数据$\mathcal{D}$和任务目标$Y$,根据概率$\mathbb{P}(Z \mid \mathcal{D})$编码网络表示为$Z$,则信息瓶颈的目标函数为:
$$\min _{\mathbb{P}(Z \mid \mathcal{D})} \operatorname{IB}_{\beta}(\mathcal{D}, Y ; Z):=[-I(Y ; Z)+\beta I(\mathcal{D} ; Z)]$$
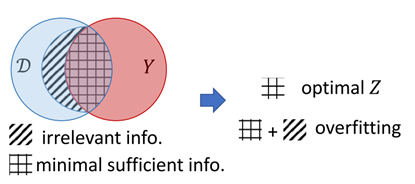
图1 信息瓶颈示意图
如图1所示,信息瓶颈准则激励表示$Z$尽可能捕获对任务目标$Y$有益的信息(sufficient的,图1中由方格阴影表示),同时尽可能去除输入$\mathcal{D}$中与任务目标无关的部分(minimal)。这种类似“提纯”的做法即“瓶颈”的含义,它使得训练的模型能够天然地避免过拟合并且对对抗性攻击变得更加鲁棒。
由于互信息的计算十分困难,在实际应用中不可能以上述公式为目标函数进行优化,常见的做法是计算互信息的上/下界作为目标函数进行优化。
图信息瓶颈(GIB)
图任务的输入数据包括节点属性和图结构,即$\mathcal{D}=(A, X)$。GIB继承了IB的基本思想,即同时从节点属性和图结构中捕获最小充分信息,如图2所示。但是也面临着两大挑战:(1)一般的基于IB的模型都会假设样本是独立同分布的,而独立同分布的假设对图中的节点不成立;(2)图结构信息对于图任务来说是不可或缺的,但是这种信息是离散的,故而难以优化。

图2 图信息瓶颈示意图
为了解决节点属性不是独立同分布的问题,本文引入了“局部依赖”假设:给定节点$v$一定距离内的邻居信息,图的其他部分和节点$v$是独立的。这一假设被用于约束$\mathbb{P}(Z \mid \mathcal{D})$的解空间。
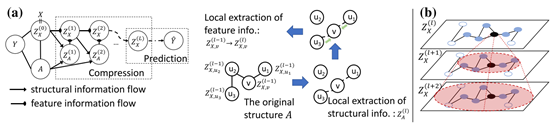
图3 GIB的局部依赖假设
对于图结构信息的利用,本文给出了一种马尔可夫依赖(如图3(a)所示):每个节点表示基于邻居结构$Z_A^{(l)}$迭代地调整,而$Z_A^{(l)}$是由上次迭代产生的表示$Z_X^{(l-1)}$和原始图结构$A$迭代融合产生的。(这里即通常讨论GNN时所谓的消息传播机制在本文中的体现)$Z_A^{(l)}$和$Z_X^{(l)}$的计算都应用了上述的局部依赖假设,即只考虑目标节点$\mathcal{T}$-跳内的节点。如图3(b)所示,$\mathcal{T}=2$时,认为黑色节点和白色节点在$l+1$次迭代时的表示$Z_X^{(l)}$是独立的,但是在$l+2$次迭代时二者之间可能会形成相关性。最终将第$L$次迭代的表示$Z_X^{(l)}$用于目标任务,则GIB的目标函数可写为:
$$\min _{\mathbb{P}\left(Z_{X}^{(L)} \mid \mathcal{D}\right) \in \Omega} \operatorname{GIB}_{\beta}\left(\mathcal{D}, Y ; Z_{X}^{(L)}\right) \triangleq\left[-I\left(Y ; Z_{X}^{(L)}\right)+\beta I\left(\mathcal{D} ; Z_{X}^{(L)}\right)\right]$$
这样只需优化两类分布:$\mathbb{P}\left(Z_{X}^{(l)} \mid Z_{X}^{(l-1)}, Z_{A}^{(l)}\right)$ 和$\mathbb{P}\left(Z_{A}^{(l)} \mid Z_{X}^{(l-1)}, A\right)$,$l \in[L]$。
GIB的变分边界(推导见原文附加材料)
(1)$I\left(Y ; Z_{X}^{(L)}\right)$的上界:对任意$v$的分布$\mathbb{Q}_{1}\left(Y_{v} \mid Z_{X, v}^{(L)}\right)$和$\mathbb{Q}_{2}\left(Y\right)$,下式成立:
$$I\left(Y ; Z_{X}^{(L)}\right) \geq 1+\mathbb{E}\left[\log \frac{\prod_{v \in V} \mathbb{Q}_{1}\left(Y_{v} \mid Z_{X, v}^{(L)}\right)}{\mathbb{Q}_{2}(Y)}\right]+\mathbb{E}_{\mathbb{P}(Y) \mathbb{P}\left(Z_{X}^{(L)}\right)}\left[\frac{\prod_{v \in V} \mathbb{Q}_{1}\left(Y_{v} \mid Z_{X, v}^{(L)}\right)}{\mathbb{Q}_{2}(Y)}\right]$$
(1)$I\left(\mathcal{D} ; Z_{X}^{(L)}\right)$的下界:选两组索引$S_{X}, S_{A} \subset[L]$,由马尔可夫依赖可知$\mathcal{D} \perp Z_{X}^{(L)} \mid\left\{Z_{X}^{(l)}\right\}_{l \in S_{X}} \cup\left\{Z_{A}^{(l)}\right\}_{l \in S_{A}}$,且对任意分布$\mathbb{Q}\left(Z_{X}^{(l)}\right), l \in S_{X},$ 和$\mathbb{Q}\left(Z_{A}^{(l)}\right), l \in S_{A}$有下式成立:
$$I\left(\mathcal{D} ; Z_{X}^{(L)}\right) \leq I\left(\mathcal{D} ;\left\{Z_{X}^{(l)}\right\}_{l \in S_{X}} \cup\left\{Z_{A}^{(l)}\right\}_{l \in S_{A}}\right) \leq \sum_{l \in S_{A}} \mathrm{AIB}^{(l)}+\sum_{l \in S_{X}} \mathrm{XIB}^{(l)},$$
$$\mathrm{AIB}^{(l)}=\mathbb{E}\left[\log \frac{\mathbb{P}\left(Z_{A}^{(l)} \mid A, Z_{X}^{(l-1)}\right)}{\mathbb{Q}\left(Z_{A}^{(l)}\right)}\right], \mathrm{XIB}^{(l)}=\mathbb{E}\left[\log \frac{\mathbb{P}\left(Z_{X}^{(l)} \mid Z_{X}^{(l-1)}, Z_{A}^{(l)}\right)}{\mathbb{Q}\left(Z_{X}^{(l)}\right)}\right]$$
注意$S_{X}$不能为空集,且若$S_{X}$中最大索引为$l$则$S_{A}$应包含$[l+1,L]$中所有索引。
GIB的使用示例
本文给出了两个利用GIB的示例:GIB-Cat和GIB-Bern。这两个方法都满足Algorithm 1所示的框架。第三步的邻居采样应用了图注意力机制网络(GAT)来计算目标节点邻居(由计算的多跳邻居)的注意力。GIB-Cat将注意力值作为分类分布的参数从多跳邻居中采样k个节点构成$Z_{A,v}^{(l)}$(见Algorithm 2),而GIB-Bern则是将注意力值(softmax替换为sigmoid)作为对邻居分别独立采样的伯努利分布的参数(见Algorithm 3)。第三步使用了Gumbel-softmax的重参数化技巧。



优化时使用变分边界代替互信息目标函数。对于计算AIB,需要确定$Z_A \sim \mathbb{Q}\left(Z_{A}\right)$。GIB-Cat假设$ Z_{A, v}=\cup_{t=1}^{\mathcal{T}}\left\{u \in V_{v t} \mid u \stackrel{\text { iid }}{\sim} \operatorname{Cat}\left(\frac{1}{\left|V_{v t}\right|}\right)\right\}$, 对于不同的$u$和$v$,$Z_{A,u}$和$Z_{A,v}$独立;GIB-Bern假设$Z_{A, v}=\cup_{t=1}^{\mathcal{T}}\left\{u \in V_{v t} \mid u \stackrel{\text { iid }}{\sim}\right.$ Bernoulli $\left.(\alpha)\right\}$,$\alpha$为超参。则AIB的经验估计为:
$$\widehat{\mathrm{AIB}}^{(l)}=\mathbb{E}_{\mathbb{P}\left(Z_{A}^{(l)} \mid A, Z_{X}^{(l-1)}\right)}\left[\log \frac{\mathbb{P}\left(Z_{A}^{(l)} \mid A, Z_{X}^{(l-1)}\right)}{\mathbb{Q}\left(Z_{A}^{(l)}\right)}\right]$$
对于计算XIB,需要确定$Z_X \sim \mathbb{Q}\left(Z_{X}\right)$。假设$Z_{X, v} \sim \sum_{i=1}^{m} w_{i} \operatorname{Gaussian}\left(\mu_{0, i}, \sigma_{0, i}^{2}\right)$,其中的参数可学习。则XIB的估计为:
$$\widehat{\mathrm{XIB}}^{(l)}=\log \frac{\mathbb{P}\left(Z_{X}^{(l)} \mid Z_{X}^{(l-1)}, Z_{A}^{(l)}\right)}{\mathbb{Q}\left(Z_{X}^{(l)}\right)}=\sum_{v \in V}\left[\log \Phi\left(Z_{X, v}^{(l)} ; \mu_{v}, \sigma_{v}^{2}\right)-\log \left(\sum_{i=1}^{m} w_{i} \Phi\left(Z_{X, v}^{(l)} ; \mu_{0, i}, \sigma_{0, i}^{2}\right)\right)\right]$$
对目标函数,使用以下替换规则:
$$I\left(\mathcal{D} ; Z_{X}^{(L)}\right) \rightarrow \sum_{l \in S_{A}} \widehat{\mathrm{AIB}}^{(l)}+\sum_{l \in S_{X}} \widehat{\mathrm{XIB}}^{(l)}$$
$$I\left(Y ; Z_{X}^{(L)}\right) \rightarrow-\sum_{v \in V} \operatorname{Cross-Entropy}\left(Z_{X, v}^{(L)} W_{\text {out }} ; Y_{v}\right)$$
实验
(1)鲁棒性验证:使用Nettack的设置,两种测试模式:模型训练后攻击(Evasive)和模型训练前攻击(Poisoning)。攻击方式:节点属性部分置反,增加或删除边。使用Transductive的训练方式。见表1.

Poisoning模式下GIB模型在Citeseer效果较差可能是因为该数据集大多数节点度都很小。
(2)消融实验:
比较GIB目标函数不同部分对结果的影响。见表2.
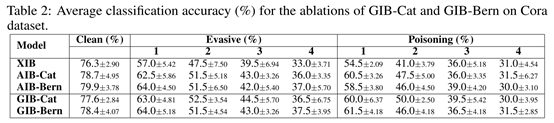
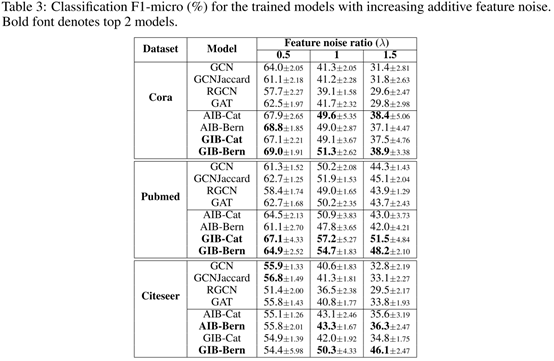
(3)仅对节点属性攻击:
验证IB对属性的影响。见表3。
思考
作者在文中留下的问题包括:GIB是否有更好的实践方法,尤其是在捕获离散的结构信息方面?做全局的聚合时,GIB能否突破局部依赖假设的限制?GIB能否用于链路预测或图分类等其他图任务?
我的问题:对于无属性图,GIB该如何定义?对于面向结构模式的任务,GIB是否有效?



