论文笔记 —— Role Discovery in Networks

Paper: Rossi R A , Ahmed N K . Role Discovery in Networks[J]. IEEE Transactions on Knowledge and Data Engineering, 2015, 27(4):1112-1131.

个人认为，这里的“角色”之所以叫“角色”，是因为现实中网络的形成一定程度上是角色驱动的，如老师与学生、上司与下属等，其在网络中的结构会有明显的区别。而角色在网络形成中的功能还有待发掘，这也是这个研究方向的意义所在。

1 角色等价问题

网络中的角色问题，即网络中节点的结构等价性（Structural equivalence）问题。假设给定图$G = (V, E)$，$r(u)$和$r(v)$分别表示节点$u$和$v$的角色，那么角色问题可表述为：

$\forall u,v \in V, r(u) = r(v) \iff u \equiv v.$

这里的等价性考虑结构等价性，即两节点的邻居完全相同：$\mathcal{N}(u) = \mathcal{N}(v)$。

但是，结构等价的条件过于严苛，在现实网络中基本不可用，因此考虑对角色等价的等价条件松弛化。

1.1 自同构等价（Automorphic equivalence）

图的同构是指对从一个图到另一个图的映射$p$,若$u$和$v$存在关系（边），则$p(u)$和$p(v)$亦存在关系。自同构即指映射$p$是从一个图到该图自身的映射。则节点$u$和节点$v$是自同构等价的，即指存在自同构映射$p$使得$u = p(v)$。显然结构等价是一种自同构等价。自同构等价是对结构等价的一种松弛，因为结构等价要求一个节点在保持连接关系的情况下可被另一节点替换，而自同构等价仅要求节点集作为子图可被替换。

1.2 规则等价 （Regular equivalence）

规则等价基于与角色等价的节点相连的节点角色相同的思路，这与结构等价要求与完全相同的节点相连不同。

1.3 随机等价 （Stochastic equivalence）

如果两节点与不同角色节点所连边的概率分布相同，则称其随机等价。

2 计算角色的方法

2.1 基于图计算角色（Graph-based Roles）的方法

基于图的角色方法是指直接从图数据计算角色的方法。

块模型：难于应用于大型网络，但可解释性强。

邻接矩阵的行/列相似性：易于计算，但可解释性差。

2.2 基于特征计算角色（Feature-based Roles）的方法

基于特征的角色方法先从图数据求得各节点的特征表示，再从特征表示计算节点等价性的方法。在基于特征表示的方法下，图中节点等价即节点的各特征表示相同。

 基于特征表示的节点等价性可松弛为节点特征的相似性。

2.3 混合方法

主要可分为先基于图后基于特征的方法和先基于特征后基于图的方法。

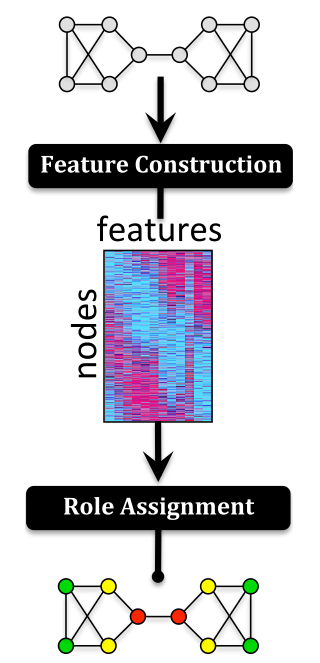
3 基于特征计算角色的框架

设图为$ G = (V, E) $ ，$X^{v}$和$X^{e}$分别表示节点和边的原始属性。

3.1 角色特征构建

特征构建系统的目标应该是生成一组特征，这些特征表征了图数据中的基本结构和重要模式。

（1）关系特征类型（Relational Feature Classes）：基于图数据选择用于计算的特征的类型

主要有四类：1. 结构特征，基于$G$；2. 边值特征，基于$(G, X^{e})$；3. 节点值特征，基于$(G, X^{v})$；4. 非关系特征。 以上四类特征都可以递归计算。

（2）角色关系特征算子（Relational Feature Operators for Roles）：决定用于构建角色特征的算子

角色关系特征算子	示例
关系聚合	MODE, MEAN, COUNT, ...
集合算子	Union, multiset, inters., ...
子图模式	k-star, k-clique, k-motif, ...
降维	SVD, PMF, NMF, ICA, PCA, ...
相似性	Cosine sim, mutual info, ...
游走	random-walks, k-walks, ...
文本分析	LDA, Link-LDA/PLSA, ...

 

（3）特征搜索策略（Feature Search Strategy）：选择在特征空间搜索特征的策略

主要有三种：全面型，引导型（启发式），随机型。

（4）关系特征选择（Relational Feature Selection: Scoring & Pruning）：决定学习过程中怎样对特征评价和简化

无监督特征选择的目标为降维和去噪。

3.1 角色分配

（1）角色聚类

（2）低秩逼近