DS博客作业04--图
0.PTA得分截图
图题目集总得分,请截图,截图中必须有自己名字。题目至少完成总题数的2/3,否则本次作业最高分5分。没有全部做完扣1分。

1.本周学习总结(0-5分)
1.1 总结图内容
1.1.1图存储结构,遍历以及运用
之前的章节我们已经开始接触到非线性结构--树,树表示的是一对多的关系,这篇博客我们要开始了解多对多的结构--图。图形结构是最普遍的一类数据结构,具有广泛的实际应用。比如说我们生活中常见的知识图谱,专业知识的路由路径搜索,解决诸多问题,图形结构是生活中不可缺少的一种结构。
(1)图的定义
- 图:指顶点集 V 和顶点间的关系:边集合E组成的数据结构。图的逻辑结构描述:Graph = (V , E),其中V表示图包含的顶点的集合,E表示定点与定点之间的关系的集合。
- 有向图和无向图
- 有向图:顾名思义,图有方向,换言之,顶点与顶点之间的边是有方向的,即带有箭头,可以从中知道是从那个点指向那个点的。比如下图就是有向图。
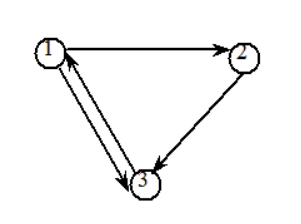
明显可以看出顶点之间的指向关系。 - 无向图:没有方向边。顶点之间只要连接就是互通的。如图:
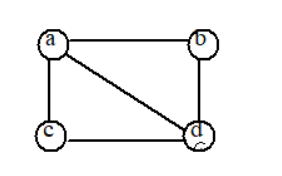
(2)图的基本术语
- 端点和邻接点
- 无向图:若存在一条边<i,j>,则称顶点i和顶点j互为邻接点。
- 有向图:存在一条边<i,j>,可知i,就之间有一条边,i点指向j点,则称此边是顶点i的一条出边,同时也是顶点j的一条入边;称顶点i 和顶点j 互为邻接点。
- 顶点的度、入度和出度
- 无向图:以顶点i为端点的边数称为该顶点的度。
- 有向图:以顶点i为终点的入边的数目,称为该顶点的入度。以顶点i为始点的出边的数目,称为该顶点的出度。一个顶点的入度与出度的和为该顶点的度。实际上也就是该点连接的边的条数。
- 边与顶点的关系:若一个图中有n个顶点和e条边,每个顶点的度为di(0≤i≤n-1),则有:e=0.5(d1+d2+d3+...+dn-1),即边的数量是各个顶点度的和的二分之一。
- 完全图:一个图中各个顶点都是互通的,我们称这样的图为完全图。
- 无向图:每两个顶点之间都存在着一条边,称为完全无向图, 包含有n*(n-1)/2条边。
- 有向图:每两个顶点之间都存在着方向相反的两条边,称为完全有向图,包含有n*(n-1)条边。
- 稠密图,稀疏图:当一个图接近完全图时,则称为稠密图。相反,当一个图含有较少的边数时,则称为稀疏图。
- 子图:顾名思义,一个图可以从另一个图拆分出来,并且不改变顶点直接的关系,这样的图成为原图的子图,子图是相对于原图来讲的。
- 路径以及路径长度:从一个顶点到另一个顶点所要经过的边叫做路径,经过边的数目之和叫做路径长度。
- 回路以及环:从一个点出发,经过了很多条路径又回到的原来的点,这条路径就是回路,又叫环。
- 连通图连通分量
- 连通图:若图中任意两个顶点都连通,否则称为非连通图。这里的连通并不止指单纯的直接连通,通过几个顶点,还能连在一起就叫做连通。
- 连通分量:在一个非连通图中,找出连通子图,这些子图之间是相互独立的,所以叫做连通分量。一般无向图中不会有连通分量。
- 无向图中,若从顶点i到顶点j有路径,则称顶点i和j是连通的。
- 有向图中若任意两个顶点之间都连通,则称此有向图为强连通图。否则,其各个强连通子图称作它的强连通分量。
- 如何寻找非强连通图中的强连通分量
- 在图中找一个有向的环
- 将其他的顶点与该环的边关系还原,如果加入了这个顶点之后,该环还是一个有向环(我的理解是环上能通到该点,该点也能返回环上),就形成新的环,依次判断每一个顶点,如果发现有的点能到了环但是无法返回,或者可以返回无法到了,就是这个图的一个强连通分量。
(3)图的存储结构
- 邻接矩阵
实际上就是一个二维数组,x,y 分别表示各个顶点,形成一个二维数组,其中保存的是边与边之间的信息,比如权值。如果两点之间没有连接,需要看i是否等于j,如果不等于,该位置值为无穷,等于的话值为0;
//图的邻接矩阵的存储类型
#define MAXV <最大顶点个数>
typedef struct
{ int no; //顶点编号
InfoType info; //顶点其他信息
} VertexType;
typedef struct //图的定义
{ int edges[MAXV][MAXV]; //邻接矩阵
int n,e; //顶点数,边数
VertexType vexs[MAXV]; //存放顶点信息
} MatGraph;
通常情况下,无向图的邻接链表是延对角线对称的,对角线上所有的位置值是0.有向图一般不会出现这样的情况。邻接矩阵的存储空间为O(n^2),一个图的邻接矩阵是唯一的,邻接矩阵适合于稠密图的存储。
- 邻接表
将各个顶点放在一个一维数组中,对图中每个顶点i建立一个单链表,将顶点i的所有邻接点链起来。就形成了邻接表。图的邻接表存储方法是一种顺序分配与链式分配相结合的存储方法。
//图的邻接表存储类型定义
typedef struct Vnode
{ Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode;
typedef struct ANode
{ int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
InfoType info; //该边的权值等信息
} ArcNode;
typedef struct
{ VNode adjlist[MAXV] ; //邻接表
int n,e; //图中顶点数n和边数e
} AdjGraph;
(4)图的创建
图是比较抽象的概念,建立图的结构并不是我们看见的图那样存在,他只是以邻接矩阵邻接表行书存在的数据而已。现在以邻接表建立为例。
void CreateAdj(AdjGraph *&G,int n,int e) //创建图邻接表
{
int i,j,a,b;
ArcNode *p;
G=new AdjGraph;
for (i=0;i<n;i++) G->adjlist[i].firstarc=NULL;//给邻接表中所有头结点的指针域置初值
for (i=1;i<=e;i++) //根据输入边建图
{ cin>>a>>b;
p=new ArcNode; //创建一个结点p
p->adjvex=b; //存放邻接点
p->nextarc=G->adjlist[a].firstarc; //采用头插法插入结点p
G->adjlist[a].firstarc=p;
}
G->n=n; G->e=n;
}
该种方法只能建立无向图,如果想建立有向图的话需要在对a对b赋值的时候进行b对a赋值。
(5)图的遍历
- 图的遍历:和树的遍历差不多,从给定图中任意指定的顶点(称为初始点)出发,按照某种搜索方法沿着图的边访问图中的所有顶点,使每个顶点仅被访问一次。这样的过程叫做图的遍历。在这里我们主要学习两种遍历方式,深度优先遍历(DFS)和广度优先遍历(BFS)。
<1>深度优先遍历 - 遍历过程如下:
- 1.从图中某个初始顶点v出发,首先访问初始顶点v。
- 2.选择一个与顶点v相邻且没被访问过的顶点w为初始顶点,再从w出发进行深度优先搜索,直到图中与当前顶点v邻接的所有顶点都被访问过为止。
就像它的名字一样,深度优先,就是不管路径是如何的。找到一条道路,使得整个图的顶点都被遍历过,这样的遍历方式就是深度优先遍历。
//对邻接表进行深度优先遍历
void DFS(ALGraph *G,int v)
{ ArcNode *p;
visited[v]=1; //置已访问标记
printf("%d ",v);
p=G->adjlist[v].firstarc;
while (p!=NULL)
{
if (visited[p->adjvex]==0) DFS(G,p->adjvex);
p=p->nextarc;
}
}
<2>广度优先遍历
- 遍历过程如下:
- 访问初始点v,接着访问v的所有未被访问过的邻接点。
- 按照次序访问每一个顶点的所有未被访问过的邻接点。
- 依次类推,直到图中所有顶点都被访问过为止。
广度优先遍历有点类似于树的层次遍历,写代码的时候需要借助队列或者栈这样的结构,来保存每一层的数据。
//采用广度优先遍历方法遍历非连通图的算法如下:
void BFS1(AdjGraph *G)
{ int i;
for (i=0;i<G->n;i++) //遍历所有未访问过的顶点
if (visited[i]==0)
BFS(G,i);
}
(6)判断图是否连通
有这样的一个问题,假如图G采用邻接表存储,设计一个算法,判断无向图G是否是联通的。该怎么做呢?求解思路如下:
- 用深度优先遍历方法,先给visited[]数组(为全局变量)置初值0,然后从0顶点开始遍历该图。
- 在一次遍历之后,若所有顶点i的visited[i]均为1,则该图是连通的;否则不连通。
//判断无向图是否连通代码:
int visited[MAXV];
bool Connect(AdjGraph *G) //判断无向图G的连通性
{ int i;
bool flag=true;
for (i=0;i<G->n;i++) //visited数组置初值
visited[i]=0;
DFS(G,0); //调用前面的中DSF算法,从顶点0开始深度优先遍历
for (i=0;i<G->n;i++)
if (visited[i]==0)
{ flag=false;
break;
}
return flag;
}
(6)简单路径问题
- <1>判断两个顶点之间是否存在简单路径
我们考虑的是是否能找到简单路径,所以要使用深度优先遍历,不在乎找到的路径是什么样子的,找到就行。
void ExistPath(AGraph *G,int u,int v,bool &has)
{ //has表示u到v是否有路径,初值为false
int w; ArcNode *p;
visited[u]=1; //置已访问标记
if (u==v) //找到了一条路径
{ has=true; //置has为true并结束算法
return;
}
p=G->adjlist[u].firstarc; //p指向顶点u的第一个相邻点
while (p!=NULL)
{ w=p->adjvex; //w为顶点u的相邻顶点
if (visited[w]==0) //若w顶点未访问,递归访问它
ExistPath(G,w,v,has);
p=p->nextarc; //p指向顶点u的下一个相邻点
}
- <2>求最短路径
假设图G采用邻接表存储,设计一个算法:求不带权无向连通图G中从顶点uv的一条最短路径(路径上经过的顶点数最少)。该使用那种遍历方式呢?这让我想到了之前的迷宫问题。广度优先遍历可以帮助找到最短的路径。广度优先遍历找到的路径一定是最短路径,而深度优先遍历则不一定。深度优先遍历能找所有路径,而广度优先遍历难以实现
void ShortPath(AdjGraph *G,int u,int v)
{ //输出从顶点u到顶点v的最短逆路径
qu[rear].data=u;//第一个顶点u进队
while (front!=rear)//队不空循环
{ front++; //出队顶点w
w=qu[front].data;
if (w==v) 根据parent关系输出路径break;
while(遍历邻接表)
{ rear++;//将w的未访问过的邻接点进队
qu[rear].data=p->adjvex;
qu[rear].parent=front;
}
}
}
1.1.2最小生成树
首先我们要了解一个概念,什么是生成树?什么是最小生成树?对于数据来说,图存储结构是不好对其进行操作的,然而将一个图变成我们熟悉的树,就方便了对数据的操作。一个连通图的生成树是一个极小连通子图,它含有图中全部n个顶点和构成一棵树的(n-1)条边。生成树是不能有回路的。如果在一颗生成树上添加一条边,那么必定构成一个环。由深度优先遍历得到的生成树称为深度优先生成树。由广度优先遍历得到的生成树称为广度优先生成树。一个图由于它的遍历方式不相同,生成的图也是不一样的,生成树有大有小。那么,对于带权连通图G来说,他有n个顶点,n-1条边。每一条边带有权值,其中权值之和最小的生成树称为图的最小生成树。如何构建最小生成树呢?
(1)普利姆算法
和之前一样,先来看看普利姆算法思路的难懂版解释是什么样子的。
- (1)初始化U={v}。v到其他顶点的所有边为候选边;
- (2)重复以下步骤n-1次,使得其他n-1个顶点被加入到U中:
- 从候选边中挑选权值最小的边输出,设该边在V-U中的顶点是k,将k加入U中;
- 考察当前V-U中的所有顶点j,修改候选边:若(j,k)的权值小于原来和顶点k关联的候选边,则用(k,j)取代后者作为候选边。
是不是看完之后似懂非懂红红火火恍恍惚惚?如何理解这个算法呢?其实很简单。总结一下:
- 首先选一个起始点放入集合U中,在与这个起始点相连接的邻接点中,选一个连边权值最小的点,加入到这个集合来。然后这两个点就形成了一个整体。
- 再在连接这个整体的所有点中,选权值最小的(离这个整体最近的点,注意,不是离单个点最近的点,而是距离整体最近的点),然后加入集合U,重复这一个步骤,知道所有的点都放进去这个集合U中。就生成了树,且是最小生成树。
//普利姆算法如下:
#define INF 32767 //INF表示∞
void Prim(MGraph g,int v)
{ int lowcost[MAXV],min,closest[MAXV],i,j,k;
for (i=0;i<g.n;i++) //给lowcost[]和closest[]置初值
{ lowcost[i]=g.edges[v][i];closest[i]=v;}
for (i=1;i<g.n;i++) //找出(n-1)个顶点
{ min=INF;
for (j=0;j<g.n;j++) // 在(V-U)中找出离U最近的顶点k
if (lowcost[j]!=0 && lowcost[j]<min)
{ min=lowcost[j]; k=j; /k记录最近顶点的编号}
printf(" 边(%d,%d)权为:%d\n",closest[k],k,min);
lowcost[k]=0; //标记k已经加入U
for (j=0;j<g.n;j++) //修改数组lowcost和closest
if (lowcost[j]!=0 && g.edges[k][j]<lowcost[j])
{ lowcost[j]=g.edges[k][j];
closest[j]=k;
}
}
}
(2)克鲁斯卡尔算法
克鲁斯卡尔(Kruskal)算法也是一种求带权无向图的最小生成树的构造性算法。先来看看他的算法过程:
- 置U的初值等于V(即包含有G中的全部顶点),TE的初值为空集(即图T中每一个顶点都构成一个连通分量)。
- 将图G中的边按权值从小到大的顺序依次选取:
- 若选取的边未使生成树T形成回路,则加入TE;
- 否则舍弃,直到TE中包含(n-1)条边为止。
克鲁斯卡尔算法的思路有点像贪心算法吧(个人觉得),主要思路也是不难理解的,将边抹去,有条件的加入边,使得生成的树为最小生成树。
void Kruskal(AdjGraph *g)
{ int i,j,k,u1,v1,sn1,sn2;
UFSTree t[MAXSize];//并查集,树结构
ArcNode *p;
Edge E[MAXSize];
k=1; //e数组的下标从1开始计
for (i=0;i<g.n;i++) //由g产生的边集E
{ p=g->adjlist[i].firstarc;
while(p!=NULL)
{ E[k].u=i;E[k].v=p->adjvex;
E[k].w=p->weight;
k++; p=p->nextarc;
}
HeapSort(E,g.e); //采用堆排序对E数组按权值递增排序
MAKE_SET(t,g.n); //初始化并查集树t
k=1; //k表示当前构造生成树的第几条边,初值为1
j=1; //E中边的下标,初值为1
while (k<g.n) //生成的边数为n-1
{ u1=E[j].u;
v1=E[j].v; //取一条边的头尾顶点编号u1和v2
sn1=FIND_SET(t,u1);
sn2=FIND_SET(t,v1); //分别得到两个顶点所属的集合编号
if (sn1!=sn2) //两顶点属不同集合
{ printf(" (%d,%d):%d\n",u1,v1,E[j].w);
k++; //生成边数增1
UNION(t,u1,v1);//将u1和v1两个顶点合并
}
j++; //扫描下一条边
}
}
1.1.3最短路径
在生活中,有时候我们会为选择的问题发愁,比如出去玩的时候,要到达某个地点,就回面临选择那条道路的问题。每个人都想又快又近的到达终点,所以,这涉及到最短路径的问题。如何求最短路径呢?这里有两种算法。分别解决单源最短路径问题和所有顶点最短路径问题。
(1)迪杰斯特拉算法
算法思路:
- a.初始化两个集合S(代表入选的顶点的集合),T(表示未选中的点的集合)
- b.在T中选取一个其距离值最小的顶点W加入S,加入之后,比较加入的点对点与点之间距离是否有改变。如果有要进行值的修改,没有则继续。重复上述步骤。
这就是迪杰斯特拉算法的大致思路,那么,转化为代码层面上来说,如何存放每个点的最短路径,如何存放最短路径长度呢?这里应用了dist[],path[]两个数组的帮助。其中 - dist[]数组存最短路径长度。
- path[]数组存最短路径。每一个path存的是前一个点,这样从后向前退就能的到完整的路径。
//迪杰斯特拉算法代码:
void Dijkstra(MatGraph g,int v)
{ int dist[MAXV],path[MAXV];
int s[MAXV];
int mindis,i,j,u;
for (i=0;i<g.n;i++)
{ dist[i]=g.edges[v][i]; //距离初始化
s[i]=0; //s[]置空
if (g.edges[v][i]<INF) //路径初始化
path[i]=v; //顶点v到i有边时
else
path[i]=-1; //顶点v到i没边时
}
s[v]=1;
for (i=0;i<g.n;i++) //循环n-1次
{ mindis=INF;
for (j=0;j<g.n;j++)
if (s[j]==0 && dist[j]<mindis)
{ u=j;
mindis=dist[j];
}
s[u]=1; //顶点u加入S中
for (j=0;j<g.n;j++) //修改不在s中的顶点的距离
if (s[j]==0)
if (g.edges[u][j]<INF &&dist[u]+g.edges[u][j]<dist[j])
{ dist[j]=dist[u]+g.edges[u][j];
path[j]=u;
}
}
Dispath(dist,path,s,g.n,v); //输出最短路径
}
(2)弗洛伊德算法
迪杰斯特拉算法好是好,但是只能解决一个点到图中其他点之间的最短路径,但是如果想知道图中每个点之间的最短路径分别是什么该怎做呢?用什么方式更加直观?有的人可能会说,既然迪杰斯特拉算法能求一个点的,多求几次,不就知道了所有点的最短路径了吗?可以这样做,不过代码量稍微大了点,这里我们引入新的算法,佛洛依德算法。
算法思路:从邻接矩阵a开始进行n次迭代,第一次迭代后a[i,j]的值是从vi到vj且中间不经过变化大于1的顶点的最短路径长度;第k次迭代后a[i,j]的值是从vi到vj且中间不经过变化大于k的顶点的最短路径长度 第n次迭代后a[i,j]的值就是从vi到vj的最短路径长度。
算法描述:
- (1) 用数组d[i][j]来记录i,j之间的最短距离。初始化d[i][j],若i=j则d[i][j]=0,
若i,j之间有边连接则d[i][j]的值为该边的权值,否则d[i][j]的值为max 。 - (2) 对所有的k值从1到n,修正任意两点之间的最短距离,计算d[i][k]+d[k][j]的值,
若小于d[i][j],则d[i][j]= d[i][k]+d[k][j],否则d[i][j]的值不变。
void Floyd(MatGraph g) //求每对顶点之间的最短路径
{ int A[MAXVEX][MAXVEX]; //建立A数组
int path[MAXVEX][MAXVEX]; //建立path数组
int i, j, k;
for (i=0;i<g.n;i++)
for (j=0;j<g.n;j++)
{ A[i][j]=g.edges[i][j];
if (i!=j && g.edges[i][j]<INF)
path[i][j]=i; //i和j顶点之间有一条边时
else //i和j顶点之间没有一条边时
path[i][j]=-1;
}
for (k=0;k<g.n;k++) //求Ak[i][j]
{ for (i=0;i<g.n;i++)
for (j=0;j<g.n;j++)
if (A[i][j]>A[i][k]+A[k][j]) //找到更短路径
{ A[i][j]=A[i][k]+A[k][j]; //修改路径长度
path[i][j]=k; //修改经过顶点k
}
}
}
1.1.4拓扑排序、关键路径
什么是拓朴排序呢?在生活我们会遇见做很多事情,那么先做什么事情,什么事情做完之后再做什么比较省时间,于此同时可以做其他什么事情,等。拓朴排序就是在一个有向图中找一个拓扑序列的过程称。该序列必须满足条件:
- 每个顶点出现且只出现一次。
- 若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
那么怎么进行拓朴排序呢?步骤如下: - 1.从有向图中选取一个没有前驱的顶点,并输出之(当然没有前驱的结点肯定不是一个,所以输出的结果也是多种多样的);
- 2.从有向图中删去此顶点以及所有以它为尾的弧,然后继续进行寻找;
- 3.重复上述两步,直至图空,或者图不空但找不到无前驱的顶点为止。
//结构体定义:
typedef struct //表头节点类型
{ vertex data; //顶点信息
int count; //存放顶点入度
ArcNode *firstarc; //指向第一条弧
} VNode;
//拓朴排序代码:
void TopSort(AdjGraph *G) //拓扑排序算法
{ int i,j;
int St[MAXV],top=-1; //栈St的指针为top
ArcNode *p;
for (i=0;i<G->n;i++) //入度置初值0
G->adjlist[i].count=0;
for (i=0;i<G->n;i++) //求所有顶点的入度
{ p=G->adjlist[i].firstarc;
while (p!=NULL)
{ G->adjlist[p->adjvex].count++;
p=p->nextarc;
}
}
for (i=0;i<G->n;i++) //将入度为0的顶点进栈
if (G->adjlist[i].count==0)
{ top++;
St[top]=i;
}
while (top>-1) //栈不空循环
{ i=St[top];top--; //出栈一个顶点i
printf("%d ",i); //输出该顶点
p=G->adjlist[i].firstarc; //找第一个邻接点
while (p!=NULL) //将顶点i的出边邻接点的入度减1
{ j=p->adjvex;
G->adjlist[j].count--;
if (G->adjlist[j].count==0) //将入度为0的邻接点进栈
{ top++;
St[top]=j;
}
p=p->nextarc; //找下一个邻接点
}
}
}
(1)事件的最早开始和最迟开始时间以及求法。
事件v最早开始时间ve(v):v作为源点事件最早开始时间为0。当v为初始源点时ve(v)=0否则ve(v)=MAX{ve(x)+a,ve(y)+b,ve(z)+c},求最早开始时间有点类似于贪心算法,求连接点最大的权值边。事件v的最迟开始时间vl(v):在不影响整个工程进度的前提下,事件v必须发生的时间称为v的最迟开始时间 。公式像这样:当v为终点时vl(v)=ve(v)否则vl(v)=MIN{vl(x)-a,vl(y)-b,vl(z)-c}。求最迟开始时间就是需要逆推。
(2)求关键路径的过程:
- 1.对有向图拓扑排序
- 2.根据拓扑序列计算事件(顶点)的ve,vl数组
ve(j) = Max{ve(i) + dut(<i,j>)}
vl(i) = Min - 3.计算关键活动的e[],l[]。即边的最早、最迟时间
e(i) = ve(j)
l(i) = vl(k) - dut(<j, k> - 4.找e=l边即为关键活动
- 5.关键活动连接起来就是关键路径
1.2.谈谈你对图的认识及学习体会。
对图的学习已经过了两周左右,刚开始老师介绍图的时候说这一部分的内容比较简单,但是我并没有这样觉得。这一部分中我学会了很多的算法,比如求最小生成树的prim算法,克鲁斯卡尔算法,还有什么狄克斯特拉算法等等,刚开始的时候看见这些算法觉得十分高级,对于算法的解释也十分高级,高级的让我读不懂。每一次预习课件总是先看一下课件中的解释,然后进行百度,看别人的博客来理解,学习。图的知识点比较综合,包含有许多之前的知识,比如树的应用,栈和队列的应用。学习本部分知识也是复习了之前学过的内容。感觉这部分拉下的有一点多了,很多的知识没有上手进行编码所以有一点生疏。
2.阅读代码(0--5分)
2.1 题目及解题代码

TreeNode* ans;
bool dfs(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == nullptr) return false;
bool lson = dfs(root->left, p, q);
bool rson = dfs(root->right, p, q);
if ((lson && rson) || ((root->val == p->val || root->val == q->val) && (lson || rson))) {
ans = root;
}
return lson || rson || (root->val == p->val || root->val == q->val);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
dfs(root, p, q);
return ans;
}
2.1.1 该题的设计思路
递归遍历整棵二叉树,定义 fx 表示 x 节点的子树中是否包含 p 节点或 q 节点,如果包含为 true,否则为 false。那么符合条件的最近公共祖先 x 一定满足如下条件:
(flson && frson) ∣∣ ((x = p ∣∣ x = q) && (flson ∣∣ frson))其中 lson 和 rson 分别代表 x 节点的左孩子和右孩子。
(1)flson && frson 说明左子树和右子树均包含 p 节点或 q 节点,如果左子树包含的是 p 节点,那么右子树只能包含 q 节点,反之亦然,因为 p 节点和 q 节点都是不同且唯一的节点,因此如果满足这个判断条件即可说明 x 就是我们要找的最近公共祖先;
(2)再来看第二条判断条件,这个判断条件即是考虑了 x 恰好是 p 节点或 q 节点且它的左子树或右子树有一个包含了另一个节点的情况,因此如果满足这个判断条件亦可说明 x 就是我们要找的最近公共祖先。
- 时间复杂度:O(N),其中 N 是二叉树的节点数。二叉树的所有节点有且只会被访问一次,因此时间复杂度为 O(N)。
- 空间复杂度:O(N),其中 N 是二叉树的节点数。递归调用的栈深度取决于二叉树的高度,二叉树最坏情况下为一条链,此时高度为 N,因此空间复杂度为 O(N)。
2.1.2 该题的伪代码
文字+代码简要介绍本题思路
bool dfs(TreeNode* root, TreeNode* p, TreeNode* q) {
如果根节点为NULL 返回flase;
lson = dfs(root->left, p, q);
rson = dfs(root->right, p, q);
如果一个节点左右孩子均包含或者x 恰好是 p 节点或 q 节点且它的左子树或右子树有一个包含了另一个节点
{
找到了最近祖先结点;
}
return lson || rson || (root->val == p->val || root->val == q->val);
}
2.1.3 运行结果
网上题解给的答案不一定能跑,请把代码复制自己运行完成,并截图。

2.1.4分析该题目解题优势及难点。
1.优势;通过一个判断语句同时考虑了两种情况,思想比较好,大大节约了代码量;
2.难点:那条判断语句不容易想明白,递归算法如果写错的话也不好找问题在哪里。
2.2 题目及解题代码
可截图,或复制代码,需要用代码符号渲染。题目截图后一定要清晰。

int trap(vector<int>& height)
{
int ans = 0;
int size = height.size();
for (int i = 1; i < size - 1; i++) {
int max_left = 0, max_right = 0;
for (int j = i; j >= 0; j--) { //Search the left part for max bar size
max_left = max(max_left, height[j]);
}
for (int j = i; j < size; j++) { //Search the right part for max bar size
max_right = max(max_right, height[j]);
}
ans += min(max_left, max_right) - height[i];
}
return ans;
}
2.2.1 该题的设计思路
暴力破解法:直接按问题描述进行。对于数组中的每个元素,我们找出下雨后水能达到的最高位置,等于两边最大高度的较小值减去当前高度的值。
- 时间复杂度: O(n^2)数组中的每个元素都需要向左向右扫描。
- 空间复杂度 O(1) 的额外空间。
2.2.2 该题的伪代码
文字+代码简要介绍本题思路
初始化 ans=0
从左向右扫描数组:
初始化 max_left=0和 max_right=0
从当前元素向左扫描并更新:
ax_left=max(max_left,height[j])
从当前元素向右扫描并更新:
max_right=max(max_right,height[j])
将min(max_left,max_right)−height[i]) 累加到 ans
2.2.3 运行结果
网上题解给的答案不一定能跑,请把代码复制自己运行完成,并截图。

2.2.4分析该题目解题优势及难点。
1.优点:暴力破解法比较直接,代码易懂;
2.缺点:面临的问题就是不太高效,没有其他方法节约时间空间;
2.3 题目及解题代码
可截图,或复制代码,需要用代码符号渲染。题目截图后一定要清晰。

int largestRectangleArea(vector<int>& heights)
{
int ans = 0;
vector<int> st;
heights.insert(heights.begin(), 0);
heights.push_back(0);
for (int i = 0; i < heights.size(); i++)
{
while (!st.empty() && heights[st.back()] > heights[i])
{
int cur = st.back();
st.pop_back();
int left = st.back() + 1;
int right = i - 1;
ans = max(ans, (right - left + 1) * heights[cur]);
}
st.push_back(i);
}
return ans;
}
2.3.1 该题的设计思路
链表题目,请用图形方式展示解决方法。同时分析该题的算法时间复杂度和空间复杂度。
1.对于一个高度,如果能得到向左和向右的边界
2.那么就能对每个高度求一次面积
3.遍历所有高度,即可得出最大面积
4.使用单调栈,在出栈操作时得到前后边界并计算面积
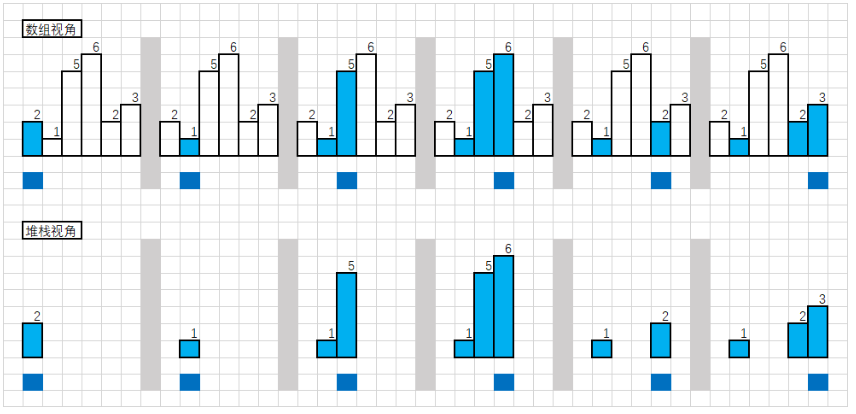
2.3.2 该题的伪代码
文字+代码简要介绍本题思路
int largestRectangleArea(vector<int>& heights)
{
定义整形变量ans = 0;
定义vector<int> st;
heights.insert(heights.begin(), 0);
heights.push_back(0);
遍历所有矩形高度
{
while (!st.empty() && heights[st.back()] > heights[i])
{
取栈顶元素
出栈;
计算left,right值;
ans = max(ans, (right - left + 1) * heights[cur]);
}
将i入栈;
}
return ans;
}
2.3.3 运行结果
网上题解给的答案不一定能跑,请把代码复制自己运行完成,并截图。

2.3.4分析该题目解题优势及难点。
1.优势:该代码思路比较好,容易理解,代码量少;
2.难点:自己想不一定能想出来,尤其是利用单调栈的做法;


