[译]探索性数据分析综述

[译]探索性数据分析综述

原文：A Comprehensive Guide to Data Exploration
作者：Sunil Ray

目录

1. 数据探索的步骤和准备

2. 缺失值处理

  • 为什么需要处理缺失值
  • Why data has missing values?
  • 缺失值处理的技术

3. 异常值检测和处理

  • What is an outlier?
  • What are the types of outliers?
  • What are the causes of outliers?
  • What is the impact of outliers on dataset?
  • How to detect outlier?
  • How to remove outlier?

4. 特征工程的艺术

  • 特征工程是什么
  • 特征工程的过程
  • 变量变换是什么
  • 怎么使用変量変换
  • 变量变换的通用方法
  • What is feature variable creation and its benefits?

1. 数据探索的步骤和准备

Garbage in, Garbage out

数据理解、处理涉及的步骤：

  1. 变量表示(Variable Identification)
  2. 单变量分析(Univariate Analysis)
  3. 多变量分析(Bi-variate Analysis)
  4. 缺失值处理(Missing values treatment)
  5. 异常值处理(Outlier treatment)
  6. 变量变换(Variable transformation)
  7. Variable creation
    最后，为了得到更好的模型，需要数次迭代步骤4-7

变量表示 Variable Identification

标识特征(Predictor, Input)和目标值(Target, output)
标识数据类型(type)和类别(category)

变量可以被定义为不同的分类：
varables-categories

单变量分析

在这个阶段，先一个个的分析变量。具体的分析方法由变量是离散的(categorical)或是连续的(continuous)决定。

连续变量：对于连续变量，需要了解它的集中趋势(central tendency)和散布情况(spread)。可以使用如下的统计指标和可视化方法：
uni-variate analysis

离散变量：对于离散变量，通常需要了解其值的频数或频率 —— Count & Count%。可以使用Bar chart 对其可视化。

多变量分析 Bi-variate Analysis

在预先定义的显著性水平上，寻找变量间的关系。变量对可以是离散的vs.离散的、连续的vs.连续的、离散的vs.连续的，具体分析方法由变量类型决定

Continuous & Continuous
分析连续变量之间的关系，我们可以直接观察变量间的散点图。对于寻找连续变量关系，这是一个简洁的方法，因为散点图展示的模式可以表示变量间的关系，而这种关系可以使线性或非线性的：
bi-variate scatter plot

散点图能够看出变量间的关系，但是无法看到具体的相关性强度。为此，引出了相关性度量(Correlation):

  • -1: 完全线性负相关
  • +1: 完全线性正相关
  • 0: 不相关

相关性可以由下式计算:
Correlation = Covariance(X,Y) / SQRT( Var(X) Var(Y))*

Categorical & Categorical

  • 双向表: 行和列分表表示两个变量，数值表示频数或频率
  • 堆叠柱状图(Stacked Column Chart): 这种方法更多的是双向表的一种可视化形式
  • 卡方检验(Chi-Square Test)
    卡方检验通常用来获得变量间关系的统计显著性，它检验样本中表现的特性是否足以反映整体中特性。卡方检验基于双向表中变量的一个或几个类别的预测频率和实际频率之间的差异，它返回指定自由度下的卡方分布的概率
    概率1：表示两个变量是相关的(dependent)
    概率0：表示两个变量是不相关的(independent)
    (待续...)

Categorical & Continuous
可以通过box plot来可视化分析离散vs连续的数据。
但如果离散变量的取值太小，则不会具有_统计显著性_。为了计算统计显著性，可以使用Z-test, T-test或者ANOVA。

  • Z-test / T-test : 评估两组变量的均值之间的差异是否具有统计意义
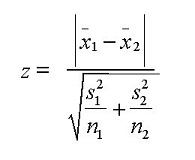
    Z-test
    如果Z的概率小于两个均值则更有意义。T检验和Z检验很相似，但它用在两个类别之间的样本小于30的情况
    T-test

  • ANOVA : 评估两组变量的均值之间的差异是否具有统计意义

2. 缺失值处理

为什么要处理缺失值

训练数据中的缺失值会降低模型的泛化能力，或者得到一个有偏差的(biased)模型，这是因为我们没有能够准确地分析变量之间的关系。这会导致预测或分类错误。

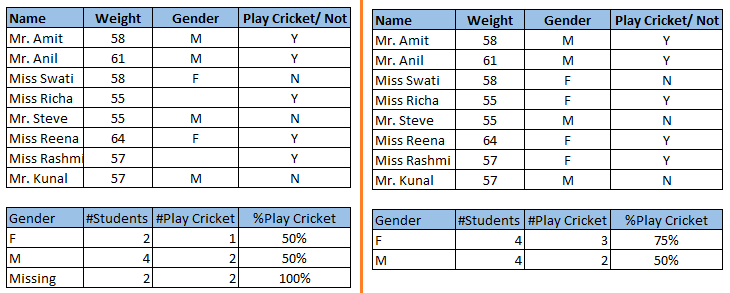
上图左右两边显示了未处理缺失值和处理缺失值的两种情况，他们会得到完全不一样的结论。

为什么数据集中出现了缺失值

在数据分析的两个阶段会产生缺失值：

  1. 数据抽取: 数据抽取过程中的错误容易产生缺失值。但这类产生缺失值错误很容易被发现并被正确的处理过程代替。
  2. 数据采集: 数据采集阶段产生的错误很难被修正，可以将其概括为以下四类：
    • 完全随机的missing
      当样本缺失的概率和所有观测值一样时。比如在调研过程中，受访者随机的回答问题
    • 随机缺失
      有时候变量缺失值产生是随机的，并且缺失频率在不同的值之间又是不一样的。例如有些情况，在女性样本中年龄和性别的缺失值会比男性的多
    • 缺失值依赖于某些未观察到的变量
      在这种情况下缺失值的产生不是随机的，而是依赖于某些我们未能观察到的(输入)变量。例如：“身体不适”会是某些特别的诊断的原因，但除非我们能把“身体不适”加入输入变量当中，否则就有可能产生“随机”的缺失。
    • 缺失值依赖于缺失值本身
      例如：那些收入很高或者非常低的人通常不会提供自己的收入信息

缺失值的处理方法

  1. 删除(Deletion)
    • 删除有缺失值的样本
    • 删除缺失值本身，然后用样本剩余数据进行训练，这样不同的变量可能会有不同的样本大小

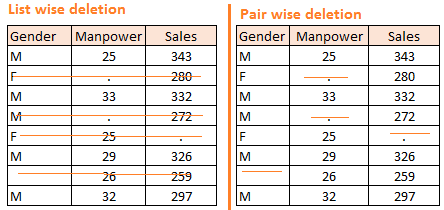
当数据缺失是随机产生时，可以考虑使用删除的方法。

  1. 均值/众数/中位数填充
    使用均值/众数/中位数填充缺失值的方法。其目标是使用能够从数据集中的有效值中识别出的关系来评估缺失值。
  • 整体填充：利用统一的指标（均值/中位数等）填充缺失值
  • 相似填充：对于其他维度相似的样本，采用相同的值进行填充。如：对于不同性别采用不同的统计量进行缺失值填充

  1. 使用预测模型
    利用预测模型对缺失值进行估计的方法。
    将不含缺失值的数据集作为训练集，含有缺失值的样本作为测试集，而含有缺失值的变量则是目标变量。可以使用回归，ANOVA，logistic回归等方法进行预测。但这种方法有两个缺点：

    1. 模型估计值通常会比实际值更加整齐(well-behaved)
    2. 如果变量间并没有关系，那么模型的预测值可能是不准确的

  2. KNN填充
    利用和包含缺失值的样本最为相似的样本的属性值填充缺失值。相似度由距离度量。

    • 优点
      • KNN能够预测定性和定量的属性
      • 不需要构建预测模型
      • 有多个缺失值的属性也很容易处理
      • 数据集中属性间的相关关系也被考虑其中
    • 缺点
      • KNN算法在处理大数据集时需要很多时间，它遍历整个数据集以寻找和目标最接近的样本
      • k值的选择对最终的结果影响很大

3. 异常值检测和处理方法

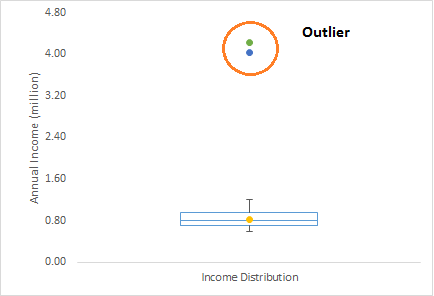
异常值

那些远离整体模式的样本

异常值类型

  • 单变量异常值：通过观察单变量的分布情况就能看到
  • 多变量异常值：n维空间中的异常值

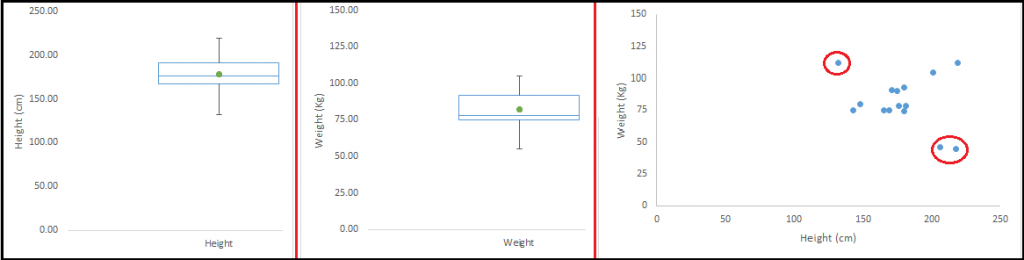
一个多变量异常值的例子：

异常的原因

不管在什么情形下碰到异常值，理想的处理方法都是找到产生异常值的原因，异常值的处理方法也依赖于异常值产生的原因。异常值产生的原因通常有两大类：

  1. 人为的错误 / Non-Natural
  2. Natural

异常值产生的具体原因：

  • 数据录入错误：数据采集过程中的人为误差
  • 测量错误：测量工具的错误产生了异常值。例如：有10个秤，其中有一个是坏的……
  • 实验误差
  • 有意的异常：这经常出现在那些调研工具中。例如：青少年通常不会填写自己实际的饮酒量，而那些如实填写的则有可能成了异常值……
  • 数据处理误差
  • 采样误差
  • Natural Outlier：这些离群点是真实的而不是由其他错误产生的

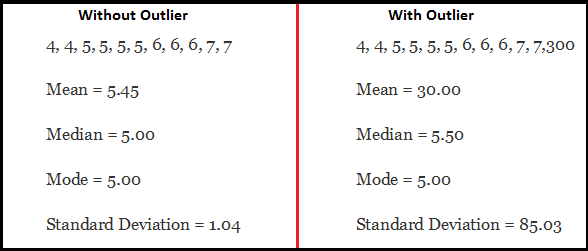
异常值的影响

异常值会显著地改变数据分析和统计建模的结果

  • 增加了错误的误差，降低了统计检验的效果(power of statistical tests)
  • 如果异常值不是随机分布的，会降低Normality
  • 异常值会对数据集本身的性质产生影响
  • 异常值会影响回归分析，ANOVA以及其他统计模型的基本假设

异常值影响统计结果的例子：

异常值检测

异常值检测的通用方法是数据可视化：Box-plot, Histogram, Scatter Plot
其他的常用规则：

  • 超过 -1.5 x IQR ~ 1.5 x IQR 的任意值
  • 覆盖方法：任何超过 小于5% 或 大于95%百分位的值都认为是异常值
  • 距离均值3倍标注差的数据点
  • 异常值检测是有影响力的数据点的特殊测试情况，其依赖于具体的商业问题理解
  • 多变量离群点通常使用影响力、权重或者距离等指标来标识，常用的指数是Mahalanobis’ distance 以及 Cook’s D

异常值处理

大部分异常值的处理方法和缺失值类似，将异常值删除、转换、二值化，将其当做一个单独的分组，填充值或者其他的统计处理方法。

删除异常样本
在异常原因是数据录入错误、数据处理错误或者异常样本很少的情况下，考虑删除异常值

变量变换和二值化
对数化能够降低数据的方差
二值化可以使得决策树能够更好地处理异常值
可以为不同的样本赋予不同的权重

填充

单独处理
如果异常值足够多，应该在统计建模时将其当做一个单独的分组。一种方法是将不同分组分开处理，分别建模，然后将结果合并起来

4. 特征工程的艺术

特征工程

特征工程是从已有数据中提取更多信息的技术(science and art)。数据并没有增加，而是使得已有的数据更加有用了。
例如从数据集的日期信息中，可以得到对应的星期信息和月份信息，这些有可能使得模型更有效。

特征工程的过程

在特征工程之前，需要完成5个探索性数据分析的步骤：

  • 变量标识
  • 单变量分析
  • 多变量分析
  • 缺失值处理
  • 异常值处理

特征工程可以分为两步：

  • 変量変换
  • 特征提取

这两个步骤在探索数据分析中都很重要，且对预测结果有显著地影响

变量变换

变量变换可以理解为改变一个变量自身的分布，或者其与其他变量之间的关系
例如：用\(\sqrt{x} 或者 \mathop{log}x\)代替x

什么时候需要変量変换

  • 当我们需要改变一个变量的取值范围 (change the scale) 或是对其进行标准化 (standardize) 以期能更好的理解变量的时候
  • 当我们能将复杂的非线性关系转换成线性关系的时候 (transform complex non-linear relationships into linear relationships)。相比于非线性的或是曲线的关系，线性关系更好理解
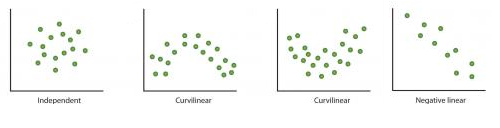
  • 对称的分布比倾斜的分布更好 (Symmetric distribution is preferred over skewed distribution)，因为它的解释性更好，并且更容易形成推论。一些建模技术需要变量是正态分布的，所以当处理一个倾斜的分布时，考虑使用变量变换降低其倾斜度。
    对于右倾斜 (right skewed)，可以使用开平方/立方、取对数的方法
    对于左倾斜 (left skewed)，可以使用取平方/立方或是指数的方法
  • 変量変换也要从具体实现的角度考虑 (implementation point of view)。例如按照实际情况，将年龄分为3个更有意义的分组等离散化 (Bining of Variables) 的方法。

常用的変量変换的方法

  • 取对数
    log常用来处理右倾斜的问题，但不能作用于负数或0

  • 开平方/立方

  • 离散化
    离散化用来分类变量，可以作用于原始数据、百分数或是频率，分类决策通常取决于具体的问题。也可以基于多个变量产生离散化的结果

特征提取及其意义

特征提取是一个基于已有特征创建新的变量/特征的过程。例如，基于时间变量可以创建其他对应的时间表示：

常用的特征提取的方法包括：

参考资料

  1. A Comprehensive Guide to Data Exploration
  2. 5 Simple manipulations to extract maximum information out of your data
  3. Dummy variable (statistics)
posted @ 2017-11-17 14:13  shencc3  阅读(1912)  评论(0)  编辑  收藏  举报