hdu4719 Oh My Holy FFF[线段树优化dp]
1|0Oh My Holy FFF
Time Limit: 5000/2500 MS (Java/Others) Memory Limit: 65535/65535 K (Java/Others)
Total Submission(s): 1047 Accepted Submission(s): 291
Problem Description
N soldiers from the famous "*FFF* army" is standing in a line, from left to right.
You, as the captain of *FFF*, want to divide them into smaller groups, but each group should still be continous in the original line. Like this:
In your opinion, the number of soldiers in each group should be no more than L.
Meanwhile, you want your division be "holy". Since the soldier may have different heights, you decide that for each group except the first one, its last soldier(which is the rightmost one) should be strictly taller than the previous group's last soldier. That is, if we set bi as the height of the last soldier in group i. Then for i >= 2, there should be bi > bi-1.
You give your division a score, which is calculated as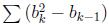 , b0 = 0 and 1 <= k <= M, if there are M groups in total. Note that M can equal to 1.
, b0 = 0 and 1 <= k <= M, if there are M groups in total. Note that M can equal to 1.
Given the heights of all soldiers, please tell us the best score you can get, or declare the division as impossible.
You, as the captain of *FFF*, want to divide them into smaller groups, but each group should still be continous in the original line. Like this:
In your opinion, the number of soldiers in each group should be no more than L.
Meanwhile, you want your division be "holy". Since the soldier may have different heights, you decide that for each group except the first one, its last soldier(which is the rightmost one) should be strictly taller than the previous group's last soldier. That is, if we set bi as the height of the last soldier in group i. Then for i >= 2, there should be bi > bi-1.
You give your division a score, which is calculated as
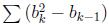 , b0 = 0 and 1 <= k <= M, if there are M groups in total. Note that M can equal to 1.
, b0 = 0 and 1 <= k <= M, if there are M groups in total. Note that M can equal to 1.Given the heights of all soldiers, please tell us the best score you can get, or declare the division as impossible.
Input
The first line has a number T (T <= 10) , indicating the number of test cases.
For each test case, first line has two numbers N and L (1 <= L <= N <= 105), as described above.
Then comes a single line with N numbers, from H1 to Hn, they are the height of each soldier in the line, from left to right. (1 <= Hi <= 105)
For each test case, first line has two numbers N and L (1 <= L <= N <= 105), as described above.
Then comes a single line with N numbers, from H1 to Hn, they are the height of each soldier in the line, from left to right. (1 <= Hi <= 105)
Output
For test case X, output "Case #X: " first, then output the best score.
Sample Input
2
5 2
1 4 3 2 5
5 2
5 4 3 2 1
Sample Output
Case #1: 31
Case #2: No solution
Source
__EOF__

本文作者:shenben
本文链接:https://www.cnblogs.com/shenben/p/6709995.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!
本文链接:https://www.cnblogs.com/shenben/p/6709995.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!
分类:
高级数据结构——线段树
, 动态规划——DP





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术