关于FFT
前置知识：
复数，单位根，多项式乘法，点值表示法，系数表示法 \(\cdots\)
单位根：
首先，我们在一个复平面中定义一个单位圆，将单位圆等分为 \(n\) 份，把位于单位圆上幅角为正且最小的向量定义为 \(n\) 次单位根，记为 \(\omega_n\)。
那我们来考虑一下单位根的奇妙性质：
首先根据复数的运算法则，两个复数相乘可以转化为复平面上的两个向量幅角相加，模长相乘，因此 \(\omega_{k=0,1,2 \cdots n}\) 实际上就是 \(\omega_n^{k=0,1,2 \cdots n}\)，当然它们也是方程 \(x^n=1\) 的根。
放一下这个经典图：
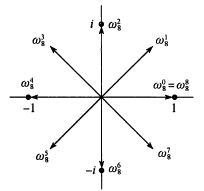
根据欧拉公式：
性质1
-
\[\omega_{2n}^{2k}=\omega_{n}^{k} \]
证明：
性质2
-
\[\omega_{n}^{\frac{n}{2}+k}=-\omega_{n}^{k} \]
证明：
性质3
-
\[ \sum\limits_{i=0}^{n-1}(\omega_n^k)^i=\left\{ \begin{aligned} n (k=0)\\ 0 (k\ne0) \end{aligned} \right. \]
证明：
当 \(k\neq 0\) 时，根据等比数列求和：
因为 \(k\neq 0\) 所以保证了上式的分母不为 \(0\)。
当 \(k=0\) 时，显然原式为 \(n\)。
多项式乘法：
定义卷积为如下的一种关系：
其中 \(i\circ j=k\) 表示一种下标运算法则，当这个关系为 \(i+j=k\) 时，这就是多项式的乘法啦。
多项式表示法：
- 系数表示法：
就是常见的多项式表示法：\(\sum\limits_{i=0}^{n-1}a_ix^i\) 这样我们会获得一个 \(\Theta(n^2)\) 多项式乘法。 - 点值表示法：
设原多项式为 \(H(x)\)，我们用 \(\{(x_0,H(x_0)),(x_1,H(x_1)),(x_2,H(x_2))\cdots(x_n,H(x_0))\}\) 来描述一个多项式，这样两个多项式 \(H(x)\) 与 \(F(x)\) 的乘积就可以很轻松的表示为 \(\{(x_0,F(x)H(x_0)),(x_1,F(x)H(x_1)),(x_2,F(x)H(x_2))\cdots(x_n,F(x)H(x_0))\}\)，对于单个点值可以 \(\Theta(n)\) 求解。
extend
为了能用点值准确描述一个函数，我们采用“插值”的方式，将点值“插”成一个多项式，常见的“插值”方法有拉格朗日插值，牛顿插值等。当然，对于一个有限的 \(n\) 次多项式，我们也可以选择 \(n+1\) 个点值代入，用待定系数法求解。
傅里叶变换
在开始之前，我们可以区分一下各种变换：
\(DFT\)：离散傅里叶变换 \(\rightarrow \Theta(n^2)\) 计算多项式乘法
\(FFT\)：快速傅里叶变换 \(\rightarrow\Theta(n\log n)\) 计算多项式乘法
\(FNTT/NTT\)：快速傅里叶变换的优化版 \(\rightarrow\) 快速数论变换，优化常数及误差
\(FWT\)：快速沃尔什变换 \(\rightarrow\) 利用类似FFT的东西解决一类卷积问题
\(FMT\)：快速莫比乌斯变化
离散傅里叶变换
我们发现常规暴力卷积复杂度是 \(\Theta(n^2)\) 的，看起来很难优化，但是用点值表示法的多项式单次乘法可以 \(\Theta(n)\) 实现，虽然带入 \(n\) 个点依然是 \(\Theta(n^2)\) 的复杂度，但至少有着优化的可能。不过，一个点值表示的多项式没有太大价值，只有系数表示法的多项式才能有更加广泛的应用。因此，这启发我们寻找这样一个算法体系解决多项式乘法：先将系数表示法转为点值表示法，优化卷积，再将结果转回系数表示法，怎么办？
傅里叶想出用 \(n\) 个模长为1的复数与点值表示法来描述多项式，而这 \(n\) 个复数选取复平面单位圆上的 \(n\) 个等分点，也就是 \(\omega_n^k(k=0,1,2\cdots n-1)\)，这样也就实现了第一步：将系数表示法转为点值表示法，这也就是 \(DFT\)（离散傅里叶变换），即：
我们设 \(\vec{a}=(a_0,a_1,a_3\cdots a_n)\) 是原多项式 \(A(x)\) 的系数表达：
那么 \(\vec{y}=(y_0,y_1,y_3\cdots y_n)\) 即为 \(DFT_n(\vec{a})\)
那为什么要带入这个 \(\omega_n^i\)？这当然是因为单位根有着优美的性质，可以很好的实现点值表示法转为系数表示法，即 \(IDFT\)（离散傅里叶逆变换）。为什么呢？这就要引出离散傅里叶变换的一个重要结论：把多项式 \(A(x)\) 的离散傅里叶变换结果作为另一个多项式 \(B(x)\) 的系数，取单位根的倒数带入 \(B(x)\)，将结果除以 \(n\) 就是 \(A(x)\) 的各项系数，我们来证明一下：
设 \(IDFT_n(\vec{y})=\vec{z}\)，则有：
根据上文关于单位根的性质3的探究，我们知道：
因此有
\(\Box\)
快速傅里叶变换
经过上述运算我们的的确确的找到了一种算法的雏形，但它的暴力插值依然是 \(\Theta(n^2)\) 的，我们来优化这个算法：
首先，我们将多项式 \(A(x)=\sum\limits_{i=0}^{n-1}a_ix^i\) 以奇偶划分开来，那么我们得到两个新的多项式 \(A_1\) 和 \(A_2\)：
显然有
这样的递推关系显然启示我们分治来解决问题，那么此时原式的 \(DFT_n(A)\) 被分治到了 \(DFT_{\frac{n}{2}}(A_1)\) 和 \(DFT_{\frac{n}{2}}(A_2)\)，这就又要利用到单位根的优美性质了，我们不妨将 \(\vec{\omega}_{\frac{n}{2}}\) 代入考虑：
对于前 \(\frac{n}{2}\) 项，有：
对于后 \(\frac{n}{2}\) 项，有：
我们发现，\(\vec{a}_n\) 的后 \(\frac{n}{2}\) 项，实际上与前 \(\frac{n}{2}\) 项满足一种类似共轭的关系，也就是说，我们只需知道前 \(\frac{n}{2}\) 项，就可以 \(\Theta(n)\) 计算出后 \(\frac{n}{2}\) 项。这样，我们成功将原问题缩减了一半的规模，接下来只要确定一个递归边界就好了，这很平凡，当 \(n=1\) 时，问题的解为 \(\omega_n^0\)，也就是 \(1\)，直接 return 即可。
具体实现时，我们把多项式的长度补到离最高项最近的 \(2\) 次幂，这样可以保证递归树高为稳定的 \(\log n\) 级别，不用担心多出来的高次项系数，它们默认为 \(0\)。
代码实现也很容易：
#include<bits/stdc++.h>
#define ld double
using namespace std;
const int N=4e6+10;
const ld pi=acos(-1.);
int n,m;
struct cpl{
ld x,y;
cpl(ld x_=0,ld y_=0){x=x_,y=y_;}
friend cpl operator+(cpl a,cpl b){return cpl(a.x+b.x,a.y+b.y);}
friend cpl operator-(cpl a,cpl b){return cpl(a.x-b.x,a.y-b.y);}
friend cpl operator*(cpl a,cpl b){return cpl(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
} a[N],b[N];
void FFT(int len,cpl *a,int opt){
if(!len) return;
cpl a1[len],a2[len];
for(int i=0;i<len;++i) a1[i]=a[i<<1],a2[i]=a[i<<1|1];
FFT(len>>1,a1,opt);
FFT(len>>1,a2,opt);
cpl w_n(cpl(cos(pi/len),opt*sin(pi/len))),w(cpl(1.,0.));
for(int i=0;i<len;++i,w=w*w_n){
int y(w*a2[i]),x(a1[i]);
a[i]=x+y,a[i+len]=x-y;
}
}
int main(){
cin>>n>>m;
for(int i=0;i<=n;++i) cin>>a[i].x;
for(int i=0;i<=m;++i) cin>>b[i].x;
for(m+=n,n=1;n<=m;n<<=1);
FFT(n>>1,a,1),FFT(n>>1,b,1);
for(int i=0;i<n;++i) a[i]=a[i]*b[i];
FFT(n>>1,a,-1);
for(int i=0;i<=m;++i) printf("%.0lf ",fabs(a[i].x/n));
return 0;
}
waring
- c++中自带
complex类，内置许多有用的函数，但实际上和手打区别不大，自行抉择即可。 - 本代码中递归使用的长度
len是折半后的长度，因次边界为len==0，而不是len==1。 - 本递归实现的代码可以在大约1.6s跑出1e6的极限数据。
至此，一个基于分治的 \(\Theta(n\log n)\) 计算卷积算法总算是成了型，这也就是所谓的“快速傅里叶变换”，即 \(FFT\)，但是此时的 \(FFT\) 尚不完善，尤其是上面的代码，肉眼可见的拉跨，我们有没有什么办法可以将其优化一下呢？
答案是肯定的。
快速傅里叶变换优化
原来的递归操作造成了许多的空间浪费，而且根据 OI 常识递归常数更大，为了降低常数，我们理应选择一种迭代的方式代替递归，那么顺着这个思路，我们应该寻找一个低复杂度的方式来将原多项式的系数向量直接变换到原递归树的底层，再一层一层向上迭代以更新答案，但是，How And Why?
位逆序置换
首先，我们来考虑第一步：如何将原多项式的系数向量直接变换到原递归树的底层。
盗一张大佬的图：
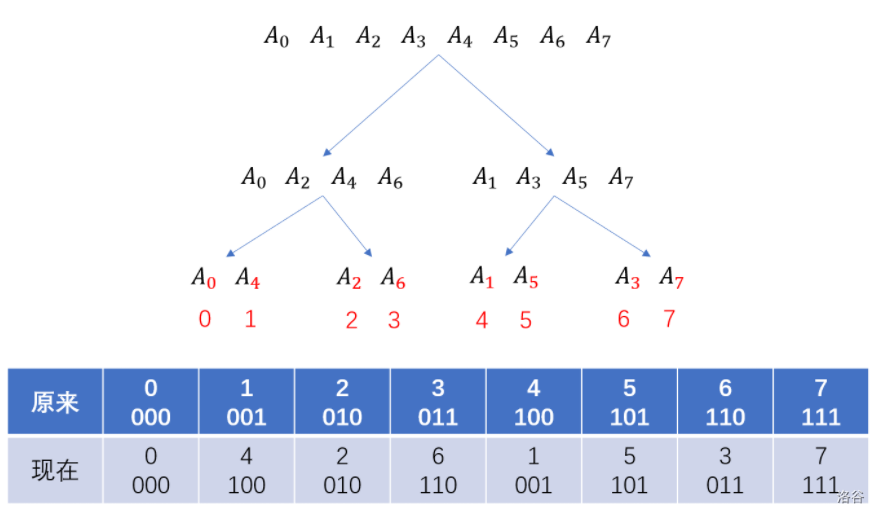
我们发现，变换后的序列实际上就是变换前序列的二进制反转，这样我们就可以不必进行奇偶下标的分类，以 \(\Theta(n)\) 的复杂度直接将原序列变换到原递归树的底层，我们称这种操作为位逆序置换。
代码实现也很简单：
int rev[(n+2)>>1];
for(i=0;i<n;i++){
rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));// bit为最高的二次幂长度
if(i<rev[i]) swap(a[i],a[rev[i]]);
}
我们考察一下上面代码的正确性：在原序列中 \(i\) 与 \(\frac{i}{2}\) 的关系是：\(i\) 可以看做是 \(\frac{i}{2}\) 的二进制上的每一位左移一位得来的，那么在反转后的数组中就需要右移一位，同时特殊处理一下奇数即可，然后我们直接 swap 一下就好啦,当然 swap 两次等于没换，所以要保证只 swap 一次。
蝴蝶操作
接下来我们来解决如何迭代的问题，这部分我们直接放代码好啦。
for(int mid=1;mid<limit;mid<<=1){
compl Wn(cos(Pi/mid),opt*sin(Pi/mid));
for(int R=mid<<1,j=0;j<limit;j+=R){
compl w(1,0);
for(int k=0;k<mid;k++,w=w*Wn){
compl x=A[j+k],y=w*A[j+mid+k];
A[j+k]=x+y,A[j+mid+k]=x-y;
}
}
}
我们再来考察一下上面代码的正确性：首先第一位枚举了待合并区间的中点（或者说是待合并区间长度的一半），接下来是单位根，然后是枚举每个区间的起点，然后枚举前半部分，然后就是区间操作区实现变换，关键在六，七行的这个“区间操作”，我们思考一下，发现实际上较底层的（或者说待合并的）区间依然满足上一次“奇偶划分”的性质，而且区间的起点顺序枚举，因此可以直接覆盖，而不用再开数组，从而减少了空间浪费。
extend
实际上“蝶形运算”与“位逆序置换”密不可分，它在 \(FFT\) 原本的应用： 信号分析中有着更加直观的体现，当然这与 \(FFT\) 在 OI 中的应用关系不大，在此不表。
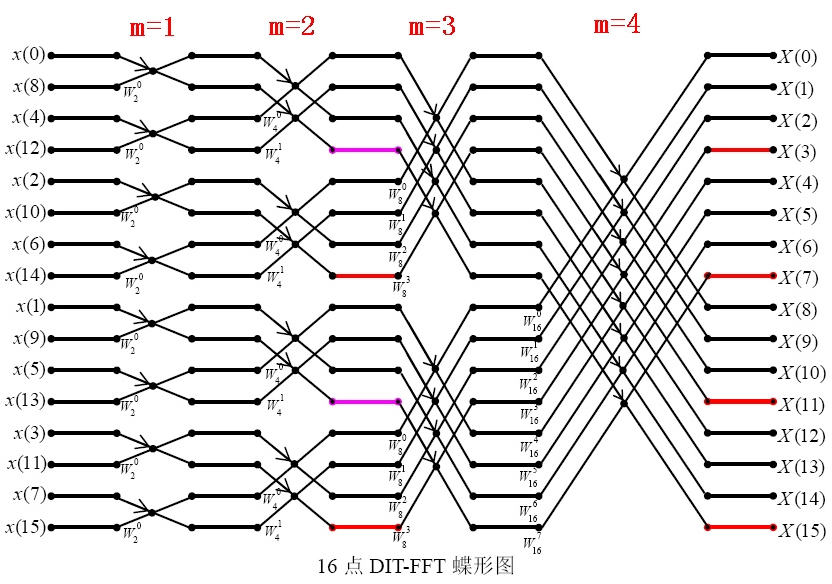
到这里我们基本上完成了常见的 \(FFT\) 优化，这也意味着你可以开始背板子了，我们来贴个代码：
#include<bits/stdc++.h>
#define ld double
using namespace std;
const int N=1e6+1;
const ld Pi=acos(-1);
struct cpl{
ld x,y;
cpl(ld x_=0,ld y_=0){x=x_,y=y_;}
friend cpl operator+(cpl a,cpl b){return cpl(a.x+b.x,a.y+b.y);}
friend cpl operator-(cpl a,cpl b){return cpl(a.x-b.x,a.y-b.y);}
friend cpl operator*(cpl a,cpl b){return cpl(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
}F[N],G[N];
int n,m,rev[N],len;
int bit(1);
void FFT(cpl *A,int limit,int opt){
for(int i=0;i<limit;++i) if(i<rev[i]) swap(A[i],A[rev[i]]);
for(int mid=1;mid<limit;mid<<=1){
cpl Wn(cos(Pi/mid),opt*sin(Pi/mid));
for(int R=mid<<1,j=0;j<limit;j+=R){
cpl w(1,0);
for(int k=0;k<mid;k++,w=w*Wn){
cpl x=A[j+k],y=w*A[j+mid+k];
A[j+k]=x+y,A[j+mid+k]=x-y;
}
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=0;i<=n;i++) cin>>F[i].x;
for(int i=0;i<=m;i++) cin>>G[i].x;
while((1<<bit)<n+m) bit++;
len=(1<<bit);
for(int i=0;i<len;++i) rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
FFT(F,len,1),FFT(G,len,1);
for(int i=0;i<=len;i++) F[i]=F[i]*G[i];
FFT(F,len,-1);
for(int i=0;i<=n+m;i++) cout<<(int)(F[i].x/len+0.5)<<' ';
return 0;
}
waring
- 因为实现过程中使用了 \(\pi\)，可能会变小的掉精问题，因此可以在最后把答案加 \(0.5\) 再向下取整把精度切回来。
- 本代码大约为递归实现速度的2~3倍。
三次变两次
原来我们进行了 \(3\) 次 \(FFT\)，分别来求 \(F(x)\) 与 \(G(x)\) 的 \(DFT\)，以及 \(F(x)*G(x)\) 的 \(IDFT\)，有没有什么方法来减少 \(FFT\) 的次数呢？有的，我们在 \(F(x)\) 实部中存 \(F(x)\) 的系数，虚部中存 \(G(x)\) 的系数，将 \(F(x)\) 进行 \(DFT\),然后求出 \(F^2(x)\)，它的虚部除以二，再 \(IDFT\) 就是答案，证明平凡：
这样我们只进行了两遍 \(FFT\)，一样得到了正确答案，常数进一步变为原来的 \(\frac{2}{3}\)，代码如下：
#include<bits/stdc++.h>
#define ld double
using namespace std;
const int N=4e6+1;
const ld Pi=acos(-1);
struct cpl{
ld x,y;
cpl(ld x_=0,ld y_=0){x=x_,y=y_;}
friend cpl operator+(cpl a,cpl b){return cpl(a.x+b.x,a.y+b.y);}
friend cpl operator-(cpl a,cpl b){return cpl(a.x-b.x,a.y-b.y);}
friend cpl operator*(cpl a,cpl b){return cpl(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
}F[N],G[N];
int n,m,rev[N],len;
int bit(1);
void FFT(cpl *A,int limit,int opt){
for(int i=0;i<limit;++i) if(i<rev[i]) swap(A[i],A[rev[i]]);
for(int mid=1;mid<limit;mid<<=1){
cpl Wn(cos(Pi/mid),opt*sin(Pi/mid));
for(int R=mid<<1,j=0;j<limit;j+=R){
cpl w(1,0);
for(int k=0;k<mid;k++,w=w*Wn){
cpl x=A[j+k],y=w*A[j+mid+k];
A[j+k]=x+y,A[j+mid+k]=x-y;
}
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=0;i<=n;i++) cin>>F[i].x;
for(int i=0;i<=m;i++) cin>>F[i].y;
while((1<<bit)<n+m) bit++;
len=(1<<bit);
for(int i=0;i<len;++i) rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
FFT(F,len,1);
for(int i=0;i<=len;i++) F[i]=F[i]*F[i];
FFT(F,len,-1);
for(int i=0;i<=n+m;i++) cout<<(int)(F[i].y/len/2.+0.5)<<' ';
return 0;
}
这样我们就获得了一个常数较小的 \(\Theta(n\log n)\) 计算卷积的算法啦，那 \(FFT\) 就告一段落了。
其他变换
